本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/database/31247.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Vue2移动端(H5项目)项目封装车牌选择组件
一、最终效果 二、参数配置
1、代码示例:
<t-keyword:isShow"isShow"ok"isShowfalse"cancel"isShowfalse"inputchange"inputchange":finalValue"trailerNo"/>2、配置参数(TKeyword Attribute…
Centos7 系统下安装go语言开发环境
该文章简述在Centos7 amd64 系统中安装go开发环境的方法。 一、golang官网查看对应平台最新的golang版本 Golang 官网地址:All releases - The Go Programming Language 二、 安装GO的过程及相关命令
# 1、下载go,这里使用 go1.22.5 版本,可…
1.Vue-cli脚手架搭建
Vue-cli脚手架搭建
视频演示地址:https://www.bilibili.com/video/BV1fCeperEzS/?vd_source0f4eae2845bd3b24b877e4586ffda69a
1.前置条件
安装node、npm
我的node版本:v16.13.1
我的npm版本:8.1.2
2.全局安装Vue-cli
安装
npm inst…
记录natapp内网穿透使用
一.客户端下载
官网地址: 点击 这里我选择windows 64 位
二,在官网 登录,配置参数
1 登录,购买免费隧道
三、配置参数
购买之后,还可以再次配置,更改端口等信息 其中authtoken很重要
四、 运行下载好的 natapp.exe
1、打开natapp.exe
2、执行命令 natapp…
【嵌入式烧录刷写文件】-2.10-为一个Intel Hex文件计算校验和Checksum
案例背景(共6页精讲):
有如下一段Intel Hex文件,为其创建Checksum校验和:CRC16,CRC32(CVN),SHA-256 Hash算法…, 将Checksum Value填充到指定地址。
:2091000058595A5B5C5D5E5F606162636465666768696A6B6C6D6E6F707172737475767…
vue通过iframe预览 pdf、word、xls、ppt、txt文件
vue通过iframe预览 pdf、word、xls、ppt、txt文件 iframe中预览只能直接打开pdf文件,其他文件需要通过office365预览。 效果:
组件代码:
<!--* fileName: 文件预览-FileView.vue* date: yanghaoxing-2024-08-16 09:32:24
!-->
<…
ECCV 2024亮点:APGCC技术刷新人群计数与定位的SOTA
摘要
在ECCV 2024会议上,一项名为APGCC的新技术以其卓越的性能引起了广泛关注。这项技术通过创新的方法,显著提高了人群计数和定位的准确性和鲁棒性,为监控、事件管理和城市规划等领域带来了新的解决方案。
正文:
随着城市化进…
leetcode-538. 把二叉搜索树转换为累加树
题目描述
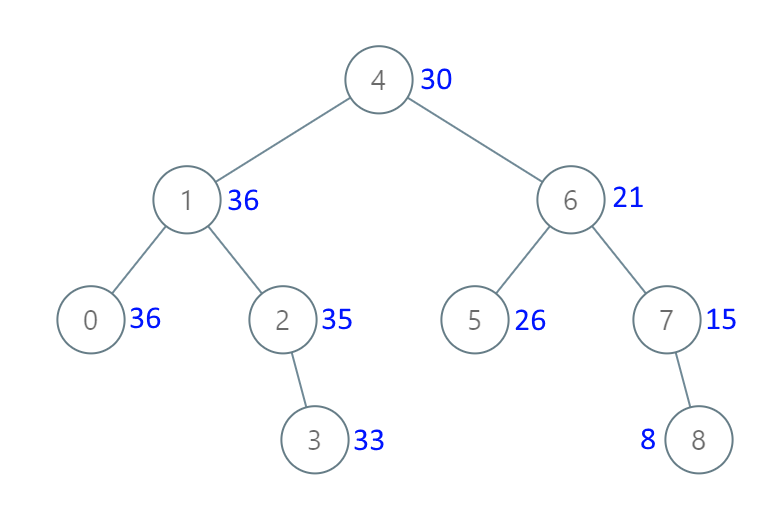
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束…
c++ | 模板进阶
前言 本篇博客讲解c中的模板的一些其他知识 💓 个人主页:普通young man-CSDN博客 ⏩ 文章专栏:C_普通young man的博客-CSDN博客 ⏩ 本人giee: 普通小青年 (pu-tong-young-man) - Gitee.com 若有问题 评论区见📝 🎉欢…
AI技术在招聘人才笔试测评中的作用
一、引言
在快速变化的商业环境中,企业之间的竞争日益激烈,而人才作为企业发展的核心驱动力,其选拔与培养显得尤为重要。传统的人才招聘流程,尤其是笔试测评环节,往往依赖于人工阅卷、主观判断,不仅效率低…
文件批量上传,oss使用时间戳解决同名问题 以及一些sql bug
1.文件批量上传 ApiOperation(value "文件批量上传")PostMapping("/multipleImageUpload")Transactional(rollbackFor Exception.class)public Result multipleImageUpload(ApiParam(name "files",value "文件",required true) R…
语言基础/分析和实践 CC++ 位域结构数据类型
文章目录 概述位域和结构体的关系位域/位段的概念位域定义的语法位段结构的利弊 结构字段的定义和存储顺序小端系统上的结构字段存储大端系统上的结构字段存储小结(承上启下) 位域结构的存储(对齐、填充、跨字节)位域结构的Bit位序…
gitlab修改默认访问端口
GitLab 自带了一个 Nginx 服务器实例,用于处理 HTTP 和 HTTPS 请求。这个内置的 Nginx 服务器被配置为与 GitLab 应用程序实例一起工作,并且它负责处理所有前端的网络通信。
通过yum或者apt安装Gitlab时,nginx通常是被自带安装并配置好的。 …
Python 中的正反斜杠用法
在Python编程中,字符串是一个常用的数据类型,字符串中的斜杠(反斜杠\和正斜杠/)具有特殊的用法和意义,本文将介绍这两种斜杠的用法。
一、反斜杠的转义作用
在Python中,反斜杠(\)被…
代码随想录算法训练营第二十一天| 669. 修剪二叉搜索树 108.将有序数组转换为二叉搜索树 538.把二叉搜索树转换为累加树
目录 一、LeetCode 669. 修剪二叉搜索树思路:C代码 二、LeetCode 108.将有序数组转换为二叉搜索树思路C代码 三、LeetCode 538.把二叉搜索树转换为累加树思路反中序遍历变量传参递归(野路子) 总结 一、LeetCode 669. 修剪二叉搜索树
题目链接…
C++的发展史及前景
🌈个人主页:Yui_ 🌈Linux专栏:Linux 🌈C语言笔记专栏:C语言笔记 🌈数据结构专栏:数据结构 🌈C专栏:C 文章目录 1. 什么是C2. C的发展史3. C的重要性3.1 C的使…
【数据结构】关于冒泡排序,选择排序,插入排序,希尔排序,堆排序你到底了解多少???(超详解)
前言: 🌟🌟Hello家人们,这期讲解排序算法的原理,希望你能帮到屏幕前的你。 🌈上期博客在这里:http://t.csdnimg.cn/I1Ssq 🌈感兴趣的小伙伴看一看小编主页:GGBondlctrl-C…
低代码平台:效率与创新的双重引擎
低代码开发在软件开发领域是一种越来越流行的趋势,这是有充分理由的。低代码使专业开发人员和非开发人员能够构建更易于集成、修改和升级的复杂企业解决方案,使企业能够快速轻松地创建软件应用程序无需丰富的编码经验。低代码平台彻底改变了软件开发方式…
7.2 算法设计与分析
分治法(考的概率较低) 回溯法(考的概率较低) 动态规划法(考的概率较高) 1