本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/database/51599.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Wophp靶场漏洞挖掘
首先进入网站发现有个搜索框,那么我们试一下xss和SQL注入
SQL注入漏洞 发现这里页面没有给我们回显 那么我们尝试sql注入 查数据库
查表 最后查出账号密码 找到账号密码之后我们去找后台登录 进入后台后发现这里有个flag
flag 接着往下翻找到一个文件上传的地方 …
Centos入门必备基础知识
CentOS(Community ENTerprise Operating System)是一个开源的Linux发行版,基于Red Hat Enterprise Linux(RHEL)源代码构建。以下是CentOS入门必备的一些基础知识:
前言 本文由浪浪云赞助发布,…
密码学---黄道十二宫
✨简单理解的概念:是一种换位密码。 🎀破解需要用到对角线的方式:第一个H,先向下移动1位,再向右移动2位,依次类推。 🎀接着对对角线重新排列,就能得到一段有序的代码 🎀 …
【Godot4自学手册】第四十七节实现火球魔法攻击
因为是自学,我想把所有能想到的都学习一遍,然后在综合一个统一的游戏。今天自学魔法攻击,单击左键发出链式火球,单击右键发射分散冰球。先看一下效果:
一、创建魔法球场景
场景根节点为Area2D节点的场景,…
HTML/CSS/JS学习笔记 Day3(HTML--C3 表格)
跟着该视频学习,记录笔记:【黑马程序员pink老师前端入门教程,零基础必看的h5(html5)css3移动端前端视频教程】https://www.bilibili.com/video/BV14J4114768?p12&vd_source04ee94ad3f2168d7d5252c857a2bf358
Day3 内容梳理:…
透明任务栏怎么设置?Windows电脑任务栏透明效果(详尽指南)
电脑任务栏可以自定义调整透明度,在Windows10和Windows11系统中,任务栏透明是默认不透明的。如果想要设置任务栏透明度,那么推荐以下方法实现,简单三个步骤即可实现,一起来看看吧! 第一步、选择合适的任务栏…
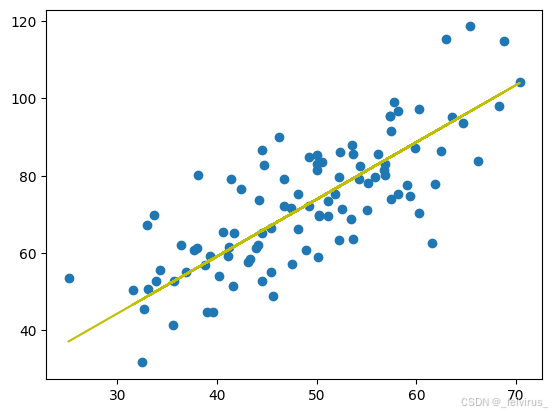
线性回归_梯度下降法
from numpy import *
import matplotlib.pyplot as plt1.导入数据
# 1.导入数据
# 模型 y wx b
points genfromtxt(linear_regress_lsm_data.csv, delimiter,)
length len(points)
print(point count %d%length)
x array(points[:, 0])
y array(points[:, 1])
plt.scatt…
react 动画_样式处理
动画
在日常开发中,页面切换时的转场动画是比较基础的一个场景
当一个组件在显示与消失过程中存在过渡动画,可以很好的增加用户的体验
在 react中实现过渡动画效果会有很多种选择,如 react-transition-group, react-motion&…
Linux 中System V IPC的共享内存
1. 概念介绍
System V IPC(Inter-Process Communication)是一组在UNIX系统中用于进程间通信的机制,包括共享内存、消息队列和信号量。这些机制由System V内核提供,并且它们的存在不依赖于创建它们的进程,而是由内核管…
el-tree父子不互相关联时,手动实现全选、反选、子级全选、清空功能
el-tree父子不互相关联时,手动实现全选、反选、子级全选、清空功能
1、功能实现图示 2、实现思路
当属性check-strictly为true时,父子节点不互相关联,如果需要全部选中或选择某一节点下的全部节点就必须手动选择每个节点,十分麻…
TI DSP下载器XDS100 V2.0无法使用问题
前言
TI DSP下载器XDS100 V2.0用着用着会突然报Error,特别是你想要用Code Composer Studio烧录下载程序的时候 查看设备管理器,发现XDS100 V2.0的设备端口莫名其妙消失了 问了淘宝的厂家,他说TI的开发板信号可能会导致调试器通信信号中断&a…
STM32常用数据采集滤波算法
例如,STM32进行滤波处理时,主要目的是处理数据采集过程中可能产生的噪声和尖刺信号。这些噪声可能来自电源干扰、传感器自身的不稳定性或其他外部因素。
1.一阶互补滤波
方法:取a0~1,本次滤波结果(1-a)本次采样值a上…
【机器学习】9 ——最大熵模型的直观理解
机器学习9 ——最大熵模型的直观理解 文章目录 机器学习9 ——最大熵模型的直观理解前奏例子硬币垃圾邮件代码 前奏
【机器学习】6 ——最大熵模型
例子
硬币
假设我们有一枚硬币,可能是公平的,也可能是不公平的。我们的任务是估计硬币的正反面出现的…
蓝桥杯备赛---1.安装软件 配置环境
1.准备比赛软件安装包 2.安装java环境 根据电脑型号选择环境,一般是x64,安装即可 3.安装STM32CubeMx 点击next默认安装即可 安装之后打开cubeMX,选择顶层Help,点击Mange embeded software packege 选择软件包添加
4.安装keil 点击…
Python | Leetcode Python题解之第402题移掉K位数字
题目: 题解:
class Solution:def removeKdigits(self, num: str, k: int) -> str:numStack []# 构建单调递增的数字串for digit in num:while k and numStack and numStack[-1] > digit:numStack.pop()k - 1numStack.append(digit)# 如果 K >…
云渲染与AI渲染分别是什么?两者的优势对比
云渲染和AI渲染是两种先进的渲染技术,它们各自具有独特的优势和应用场景。下面针对两种情况来简单说明下。 1、云渲染:
- 定义:云渲染是一种利用远程服务器(云端)来处理和生成渲染效果的技术。它允许用户将计算密集型的任务转移到云端&#…
【西电电装实习】4. 无人机系统
文章目录 前言一、定义概念 缩写定义分类 二、性质系统结构 开源平台三、使用步骤总结参考文献 前言
西电电装实习 - 无人机系统 一、定义概念 缩写
定义
无人机(Unmanned Aerial Vehicle,UAV),是无人驾驶的飞行器。它利用无…
2024121读书笔记|《不急:我们慢慢慢慢来》——做人呢,最重要的是开心
2024121读书笔记|《不急:我们慢慢慢慢来》——做人呢,最重要的是开心 1. 做人呢,最重要是开心2. 每一刻都有意义3. 世界很有趣,你怎能无趣4. 为自己活一次 《不急:我们慢慢慢慢来(暖心漫画)》曾…