本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.ldbm.cn/p/116315.html
如若内容造成侵权/违法违规/事实不符，请联系编程新知网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
![[Java]JDK8新特性](https://img-blog.csdnimg.cn/ec565e96d8b94770bedd404d2fbd5aec.png)
[Java]JDK8新特性
一、Java版本迭代概述
1.1发布特点（小步快跑，快速迭代）
发行版本发行时间备注Java 1.01996.01.23Sun公司发布了Java的第一个开发工具包Java 5.02004.09.30①版本号从1.4直接更新至5.0；②平台更名为JavaSE、JavaEE、JavaMEJava 8…
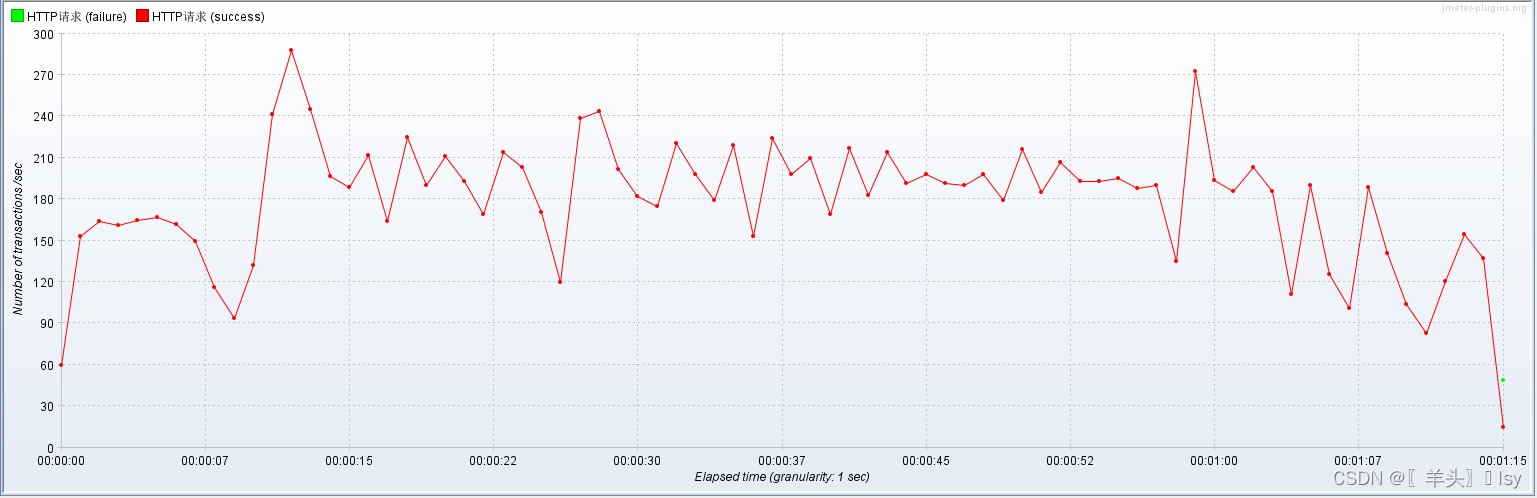
jmeter线程组 bzm - Concurrency Thread Group 阶梯式压测
简介 bzm - Concurrency Thread Group 不是JMeter的官方插件，而是一种由Blazemeter提供的高级线程组插件，它提供了更灵活的并发性能测试设置。它可以在不同的时间内并发执行不同数量的线程，模拟不同的负载场景。 插件下载地址（jme…
FFmpeg入门之Windows/Linux下FFmpeg源码编译
1.源码下载: git clone https://github.com/FFmpeg/FFmpeg.git windows : macos: ubuntu: 2.编译FFmpeg
CompilationGuide – FFmpeg windows: 1.下载yasm并安装 : Download - The Yasm Modular Assembler Project 下载后复制到c:/windows 2.下载SDL 3.下载H264/265源码
git…
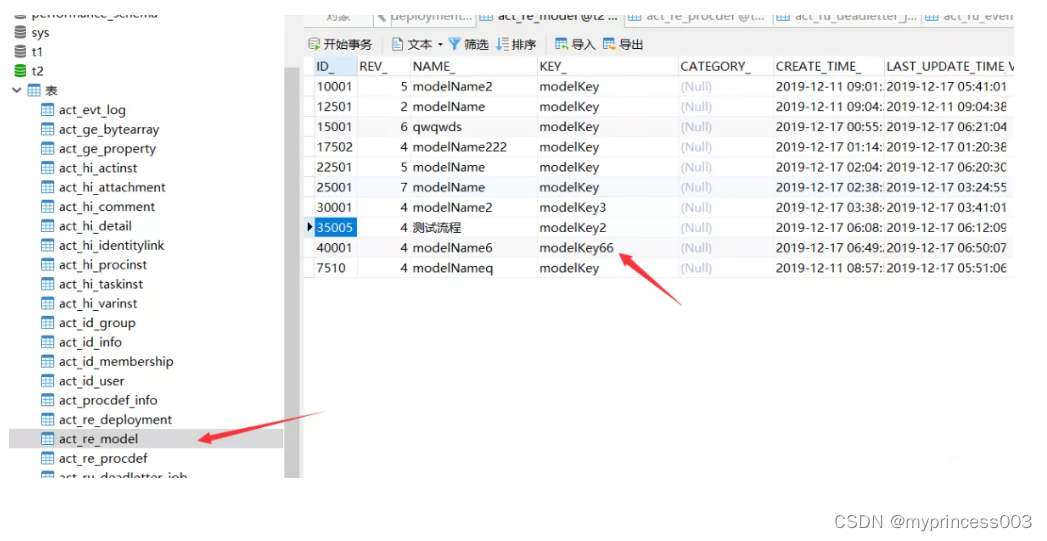
集成Activiti-Modeler流程设计器
集成Activiti-Modeler流程设计器
Activiti Modeler 是 Activiti 官方提供的一款在线流程设计的前端插件，可以方便流程设计与开发人员绘制流程图，保存流程模型，部署至流程定义等等。
1、材料准备 首先我们需要获取activiti-explorer.zip&…
高阶导数的概念与公式
目录
高阶导数的概念
常用的高阶导数的公式
隐函数补充
反函数补充 高阶导数的概念 高阶导数是指一阶或二阶及以上的导数。这些导数可以通过连续进行一阶导数的计算来得到。然而，实际计算高阶导数时，存在一些问题，例如对抽象函数高阶导数…
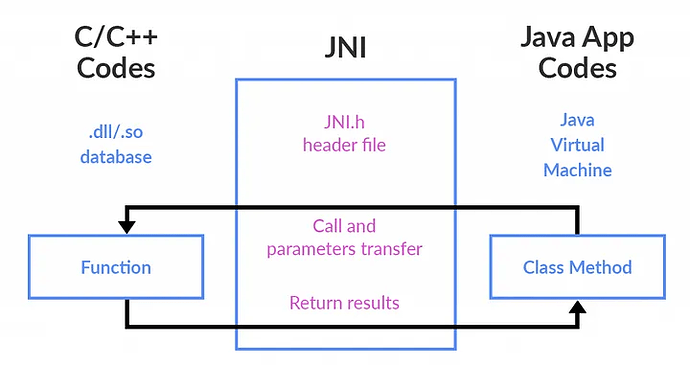
Java native 关键字
如你在看 JDK 的源代码的时候，大概率会看到很多方法使用了 native 关键字。
下面是 String 对象 JDK 中的源代码，就带有了一个 native 关键字。 native 是干什么用的
简单来说就是 Java 的 native 方法的实现不是用 Java 实现的，可能在其他…
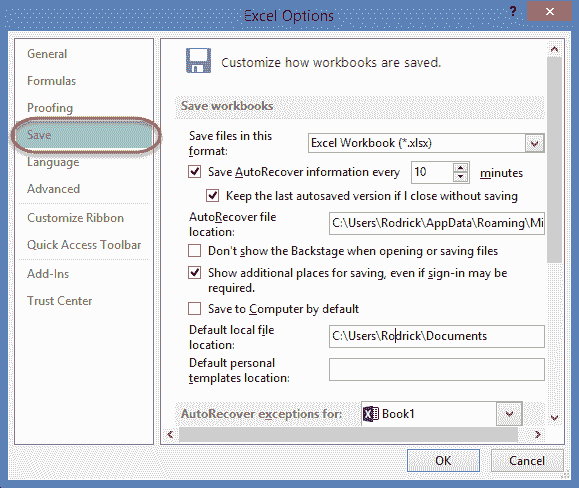
Microsoft Excel 101 简介
什么是 Microsoft Excel？
Microsoft Excel 是一个电子表格程序，用于记录和分析数值数据。 将电子表格想像成构成表格的列和行的集合。 字母通常分配给列，数字通常分配给行。 列和行相交的点称为像元。 单元格的地址由代表列的字母和代表行的…
解决gyp verb `which` failed python2 Error: not found: python2
运行老项目遇到如下报错
PS C:\Users\demo02> yarn install
yarn install v1.22.19
info No lockfile found.
[1/5] Validating package.json...
[2/5] Resolving packages...
warning axios0.18.1: Critical security vulnerability fixed in v0.21.1. For more informati…
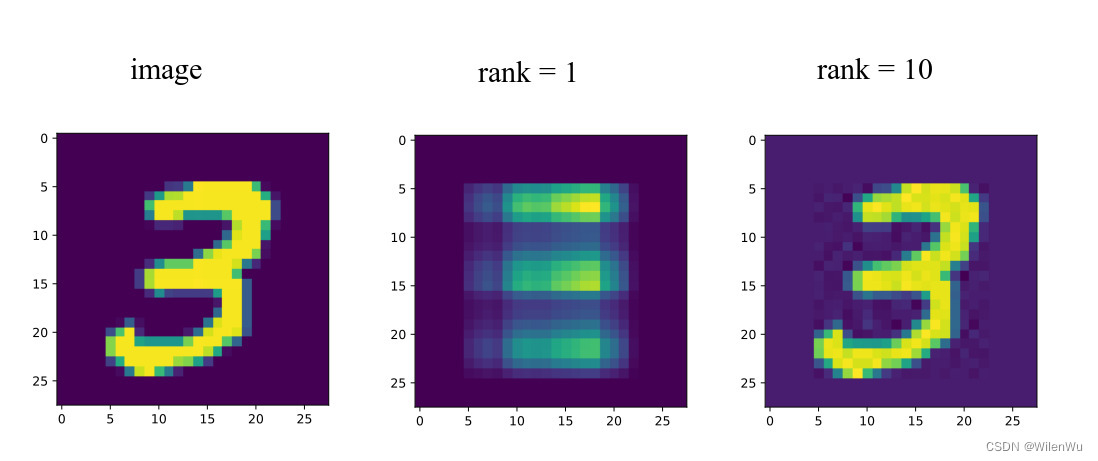
线性代数的本质(十)——矩阵分解
文章目录 矩阵分解LU分解QR分解特征值分解奇异值分解奇异值分解矩阵的基本子空间奇异值分解的性质矩阵的外积展开式 矩阵分解
矩阵的因式分解是把矩阵表示为多个矩阵的乘积，这种结构更便于理解和计算。
LU分解
设 A A A 是 m n m\times n mn 矩阵，…
springboot整合actuator、admin对应用程序进行监控
Spring Boot Actuator 是 Spring Boot 的一个子项目，可以对 Spring Boot 应用程序进行监控和管理，并对外提供了大量的端点，可以选择使用 HTTP 端点或 JMX 来管理和监控应用程序。 这篇文章主要介绍我们的应用程序中怎么加入actuator来对应用进…
解决Java类加载异常：java.lang.ClassNotFoundException
在Java开发过程中，有时会遇到类加载异常，其中之一是java.lang.ClassNotFoundException异常。这个异常通常出现在缺少相关依赖库或配置问题的情况下。本文将介绍如何解决这个问题，并以一个具体案例来说明。
问题描述
在开发过程中࿰…
SpringMVC之JSON数据返回异常处理机制
目录 前言
一、JSON数据返回
1.导入依赖
2.配置spring-mvc.xml
3.使用ResponseBody注解
4.Jackson
4.1.介绍
4.2.常用注解
二、异常处理机制
1.为什么要全局异常处理
2.异常处理思路
3.SpringMVC异常分类
4.综合案例
4.1.异常处理方式一
4.2.异常处理方式二
4.3…
《确保安全：PostgreSQL安全配置与最佳实践》
🌷🍁 博主猫头虎（🐅🐾）带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖： 🛠️ 全栈技术 Full Stack: 📚…
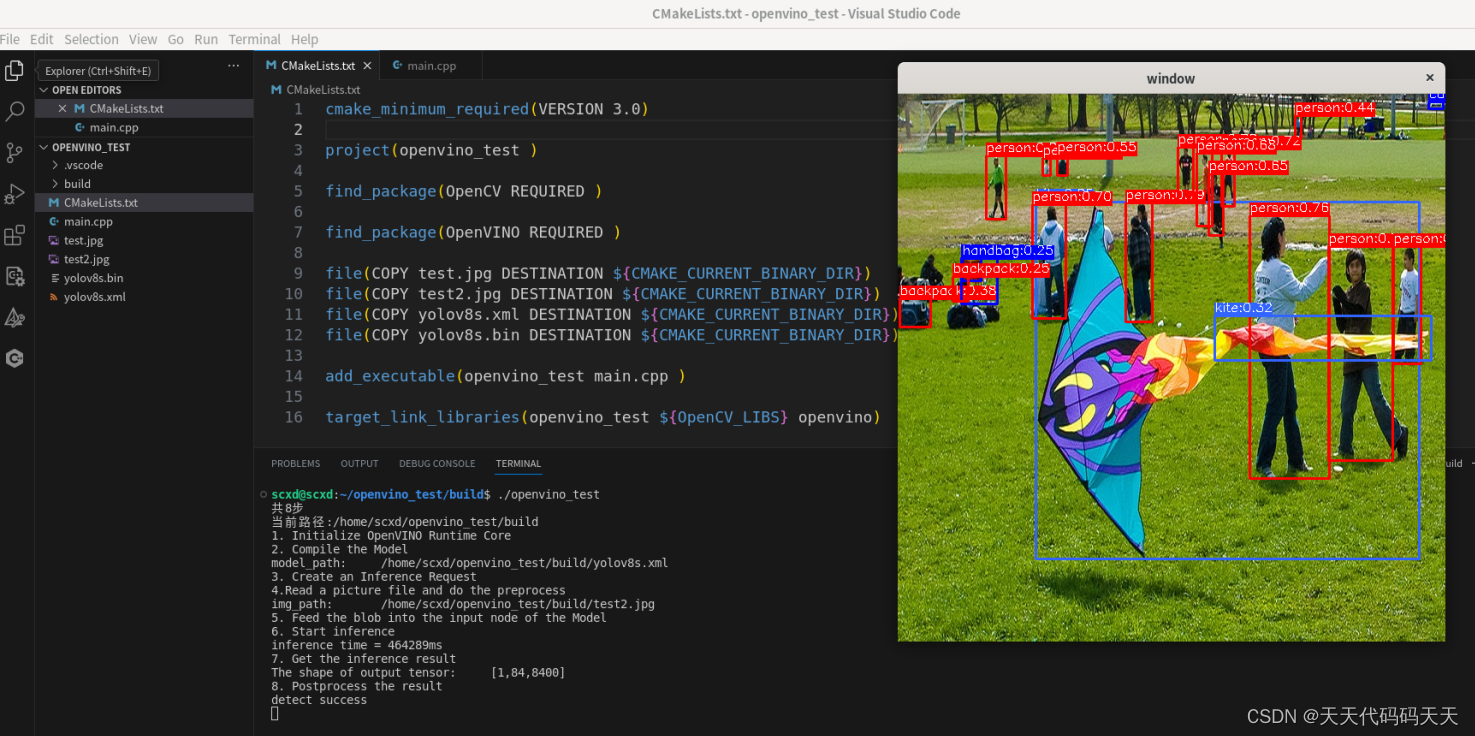
Linux C++ OpenVINO 物体检测 Demo
目录 main.cpp
#include <iostream>
#include <string>
#include <vector>
#include <openvino/openvino.hpp>
#include <opencv2/opencv.hpp>
#include <dirent.h>
#include <stdio.h>
#include <time.h>
#include …
【Java 基础篇】Java 比较器排序：精通自定义对象排序
在 Java 编程中，排序是一个非常常见且重要的操作。Java 提供了多种排序机制，其中之一就是使用比较器（Comparator）进行排序。比较器允许您自定义对象的排序方式，使您能够实现各种排序需求，从简单的对象排序到…
App Inventor 2 实现Ascii码转换（Ascii编码与解码）
之前有同学问，App Inventor 2 字符及Ascii码如何进行转换，经过调查，其原生的组件和内置块无法完成这个功能，网上也有利用Web客户端组件执行js代码来进行转换，不过逻辑稍复杂效率还不高。这里介绍一个拓展可以非常方便的…
（二十八）大数据实战——Flume数据采集之kafka数据生产与消费集成案例
前言
本节内容我们主要介绍一下flume数据采集和kafka消息中间键的整合。通过flume监听nc端口的数据，将数据发送到kafka消息的first主题中，然后在通过flume消费kafka中的主题消息，将消费到的消息打印到控制台上。集成使用flume作为kafka的生产…
Web应用开发 - 实训三 B Servlet基础
Web应用开发 - 实训三 B Servlet基础 前言： 零、前期准备准备工具创建项目导入 jar 包配置运行设置 一、实训第一部分第一张图第二张图第三张图 二、实训第二部分第一张图第二张图 前言：
eclipse 是不可能用的，并不是说它界面丑，…
点云从入门到精通技术详解100篇-从全局到局部的三维点云细节差异分析
目录 前言 国内外研究现状 细节差异分析相关研究 三维点云的相似性相关研究 存在的问题 三维点云对比的相关技术 2.1 三维点云的采集设备 2.2三维点云的存储格式 2.3三维点云的空间变换 2.4三维点云相似度分析 2.4.1点云特征的提取 2.4.2特征相似度计算 本文篇幅较长࿰…
《打造高可用PostgreSQL：策略与工具》
🌷🍁 博主猫头虎（🐅🐾）带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖： 🛠️ 全栈技术 Full Stack: 📚…