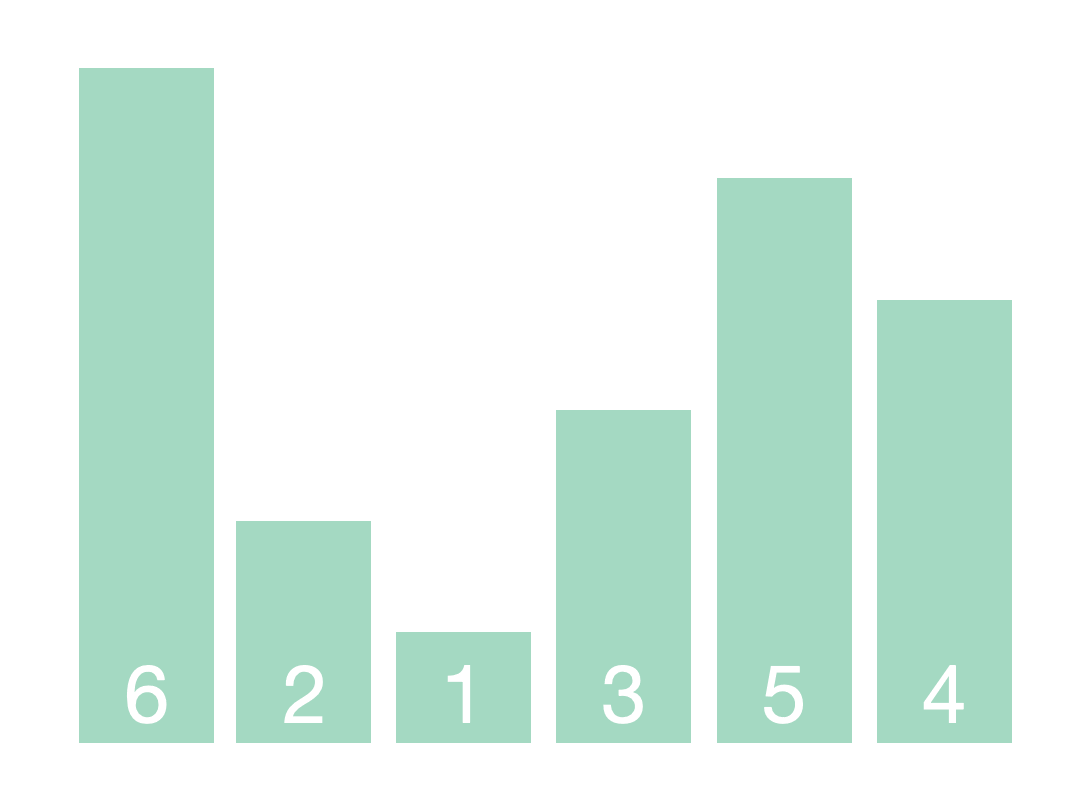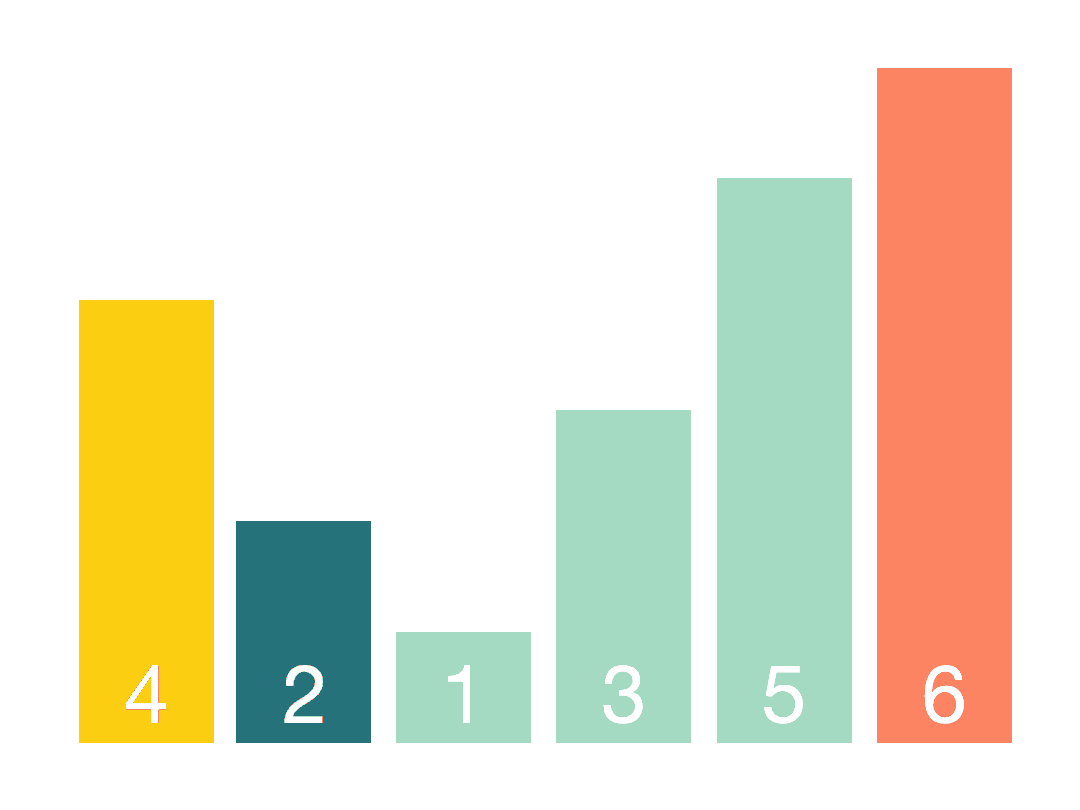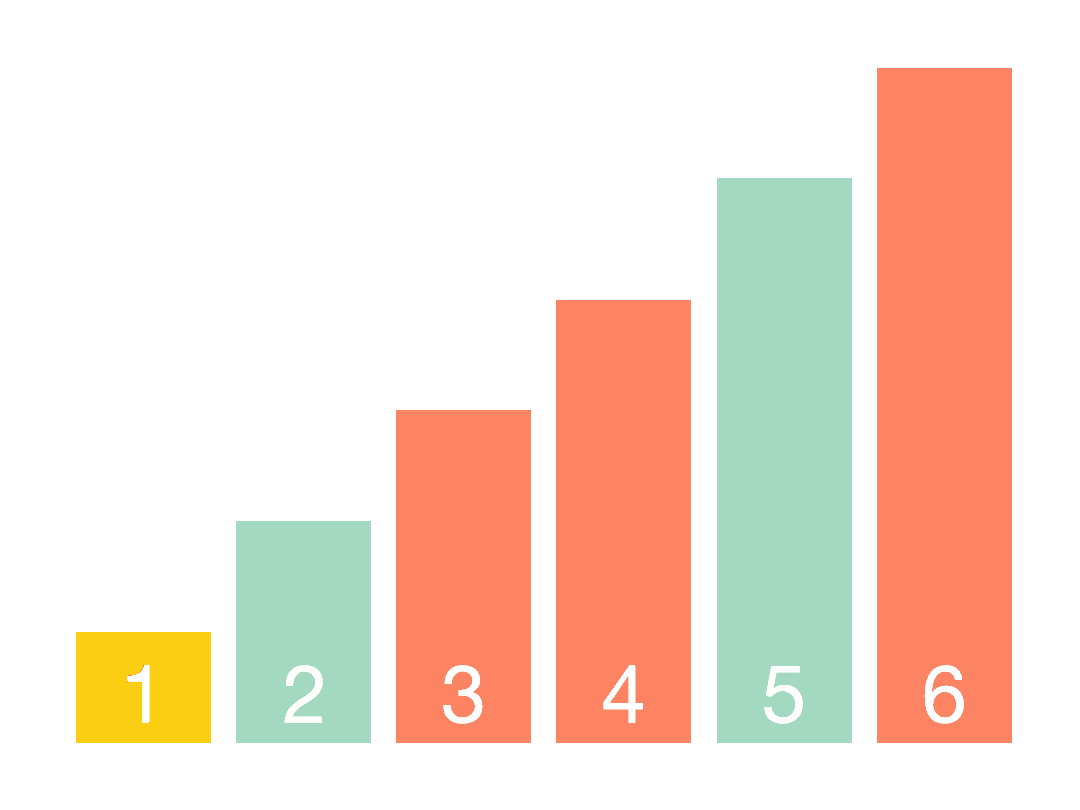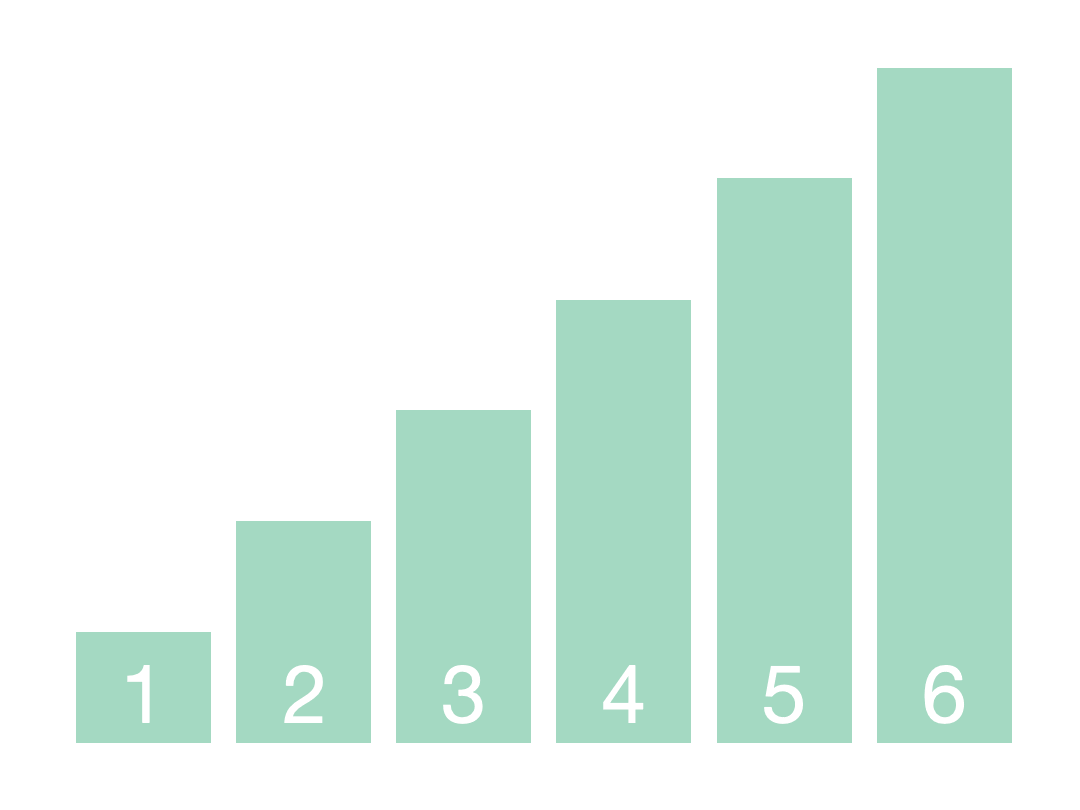本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/116540.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Java“牵手”微店商品列表页数据采集+微店商品价格数据排序,微店API接口申请指南
微店平台创立于2011年5月,是北京口袋时尚科技开发的应用,2014年1月"微店"APP正式上线。微店已经从小微店主首选的开店工具转型为助力创业者发展兴趣、创立品牌、玩成事业的系统及基础设施。
微店商品列表数据包含商品名称、价格、销量、详情、…
uni-app:实现条件判断展示图片(函数判定+三目运算)
一、多条件判断(通过函数进行图片展示)
效果 代码
在data中定义图片信息和要传递的数据信息,在src中写入函数并携带要传递的数据,通过传递的数据在函数中进行判断,并返回对应的图片信息
<template><view&…
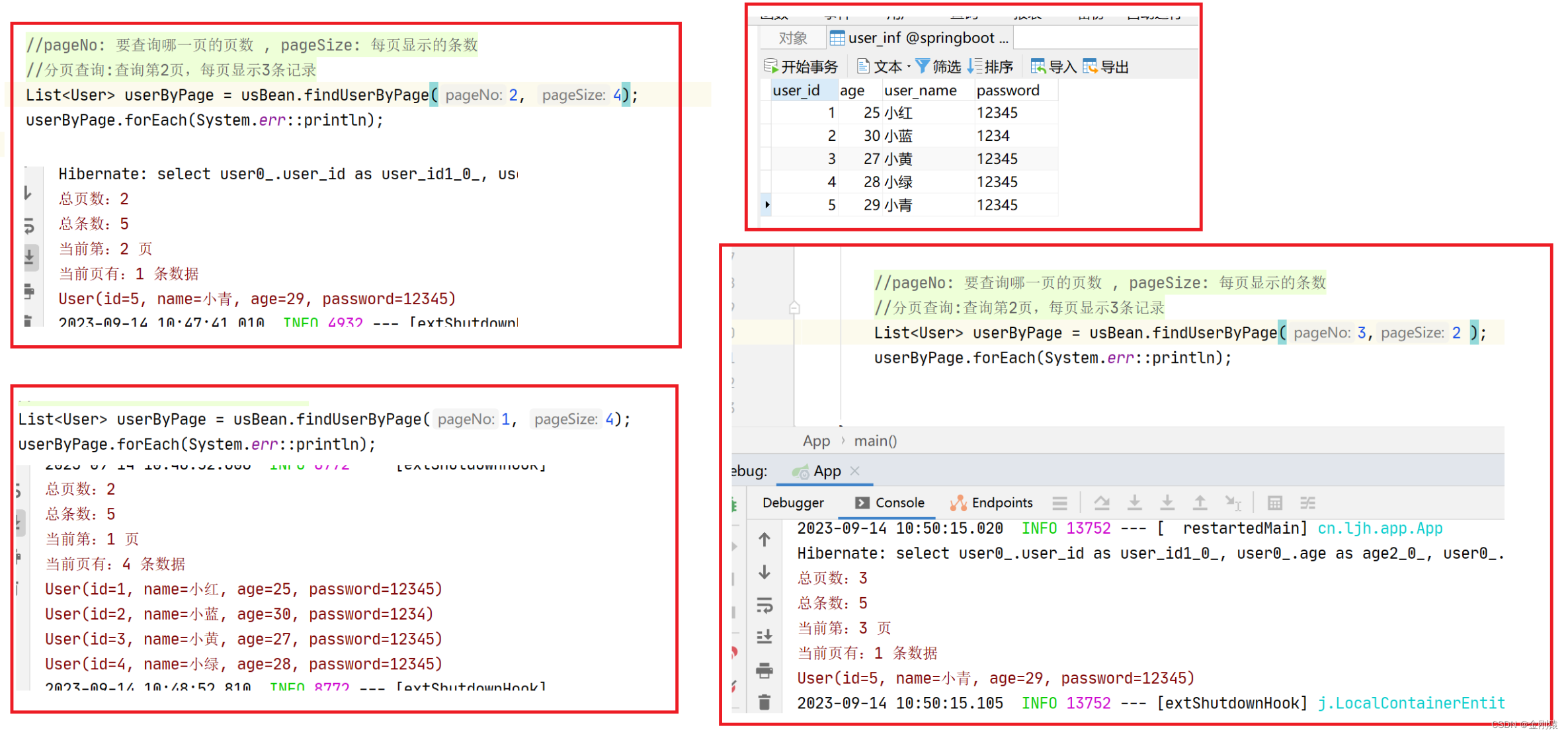
66、Spring Data JPA 的基本功能--CRUD 和 分页
Spring Data JPA 的基本功能–CRUD 和 分页
★ Spring Data JPA开发
(1)配置数据源。
(2)配置JPA相关属性,这些属性由JpaProperties类负责处理。——上面2步都在application.properties中配置即可。
(3&a…
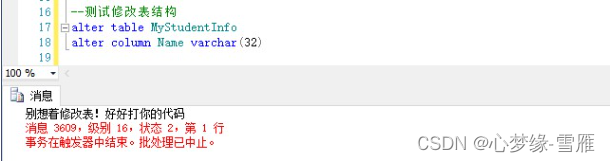
sql server 触发器的使用
看数据库下的所有触发器及状态
SELECT a.name 数据表名 ,
sysobjects.name AS 触发器名 ,
sysobjects.crdate AS 创建时间 ,
sysobjects.info ,
sysobjects.status
FROM sysobjects
LEFT JOIN ( SELECT *
FROM sysobjects
WHERE xtype U
) AS a ON sysobjects.parent_obj a.…
融合通信在电力行业中的应用
所谓电力应急,就是快速处理突发紧急事件尽量减少因供电中断造成的损失,快速修复故障设备或线路,使电力生产和运营恢复正常。重大施工事故、公共紧急事件、性质恶劣的违章操作、蓄意破坏、自然灾害等,都极易引发大规模停电事故甚至…
AI绘画:StableDiffusion实操教程-斗罗大陆-朱竹清(附高清图下载)
大家好,我是小梦,最近一直研究AI绘画。
不久前,我与大家分享了StableDiffusion的全面教程
然而,仍有些读者提出,虽然他们已经成功地安装了此工具,但生成的作品与我展示的相差较大。那么,如何缩…
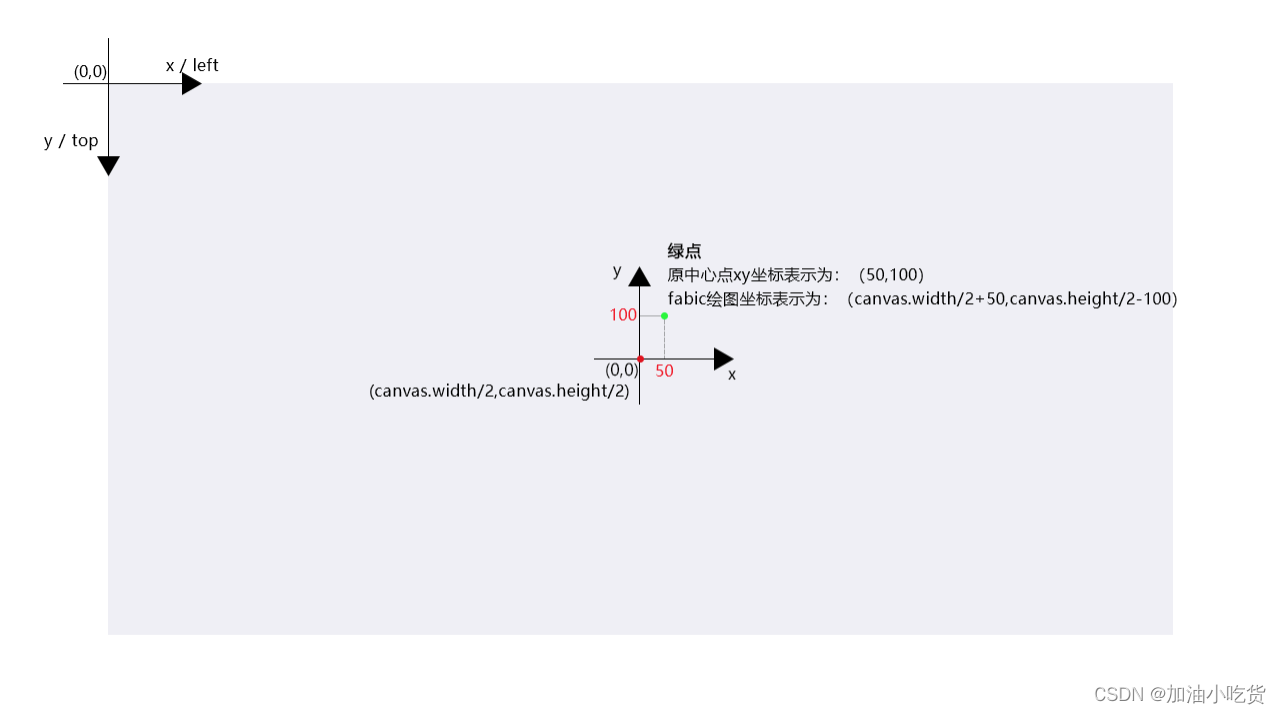
fabic如何将绘图原点移到画布中心
情况说明:
fabic默认绘图原点为left:0,top:0
后端给我的内容是按照x,y返回的,需要将坐标系移到fabic画布的中心位置,找了下网上合适的砖,想一句命令直接设置,结果没有。…
JDK、eclipse软件的安装
一、打开JDK安装包 二、复制路径 三、点击我的电脑,找到环境变量 四、新建环境 变量名:JAVA_HOME
变量值就是刚刚复制的路径
五、在path中建立新变量 双击path 打印以下文字 最后一直双击确定,安装环境完成。
六、双击eclipse 选择好安装…
二叉树的概念及存储结构
目录
1.树的概念
1.1树的相关概念
1.2树的表示与应用
2.二叉树的概念及结构
2.1二叉树的概念
2.1.1特殊的二叉树
2.2.2二叉树的性质
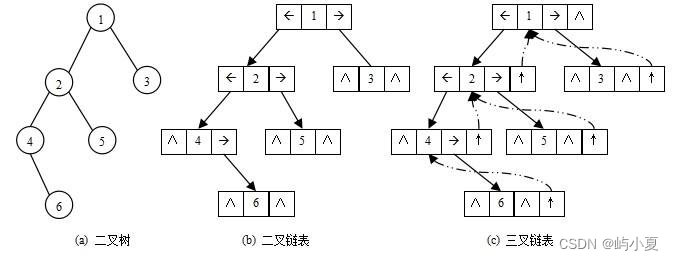
2.2二叉树的结构
2.2.1顺序存储
2.2.2链式存储 这是一篇纯理论的博客,会对数据结构中的二叉树进行详细的讲解,让你对树的能有个清晰的…
数据结构——排序算法——快速排序
快速排序算法的基本思想是 1.从数组中取出一个数,称之为基数(pivot) 2.遍历数组,将比基数大的数字放到它的右边,比基数小的数字放到它的左边。遍历完成后,数组被分成了左右两个区域 3.将左右两个区域视为两…
MFC-GetAdaptersAddresses获取网卡信息
需要:#pragma comment(lib, "IPHLPAPI.lib")
GetAdaptersAddresses函数参数说明 ULONG bufferSize = 0;ULONG result = ::GetAdaptersAddresses(AF_UNSPEC, GAA_FLAG_INCLUDE_PREFIX, nullptr, nullptr, &bufferSize);/*参数1:ULONG Family 网络协议族,此参…
亚马逊新手运营需要规避哪些风险?怎么分析竞争对手?——站斧浏览器
正所谓知己知彼才能百战不殆,分析竞争对手是运营手段之一,那么亚马逊怎么分析竞争对手?亚马逊新手运营需要规避的风险有哪些方面?
亚马逊怎么分析竞争对手
1、商品和品牌比较
(1)产品种类和范围…
LeetCode-热题100-笔记-day27
2. 二叉树的层序遍历https://leetcode.cn/problems/binary-tree-level-order-traversal/ 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例 1: 输入:root [3…
【pythonflask-1】简单实现加减乘除输入界面
app.py
import flask
from flask import Flask, render_template, request
# 计算精确的浮点结果,float加法也计算不出来
from decimal import Decimalapp Flask(__name__)app.route(/)
def home():return render_template(index.html)app.route(/calculate, meth…
(一)探索随机变量及其分布:概率世界的魔法
文章目录 🍋引言🍋什么是随机变量?🍋离散随机变量🍋连续随机变量 🍋随机变量的概率分布🍋离散概率分布🍋0-1分布(Bernoulli分布)🍋二项分布&#…
【案例教学】华为云API图像搜索ImageSearch的快捷性—AI帮助您快速归类图片
云服务、API、SDK,调试,查看,我都行
阅读短文您可以学习到:人工智能AI同类型的相片合并归类 1 IntelliJ IDEA 之API插件介绍
API插件支持 VS Code IDE、IntelliJ IDEA等平台、以及华为云自研 CodeArts IDE,基于华为云…
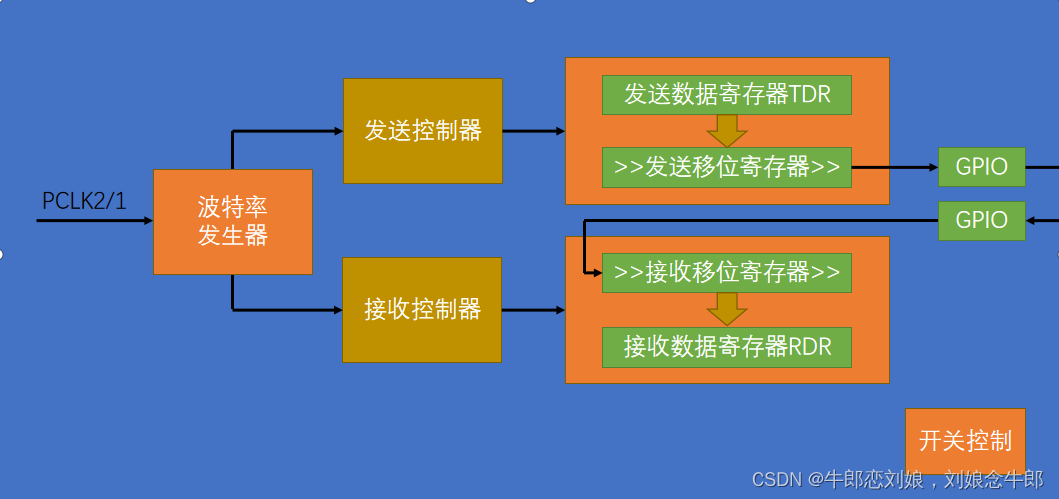
STM32f103入门(12)USART串口信息发送+接收
USART 介绍串口发送使用工具初始化发送数据接收数据 介绍 电平标准是数据1和数据0的表达方式,是传输线缆中人为规定的电压与数据的对应关系,串口常用的电平标准有如下三种:
TTL电平:3.3V或5V表示1,0V表示0 RS232电平&…
《PostgreSQL与MySQL:详细对比与分析》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…