本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/123812.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
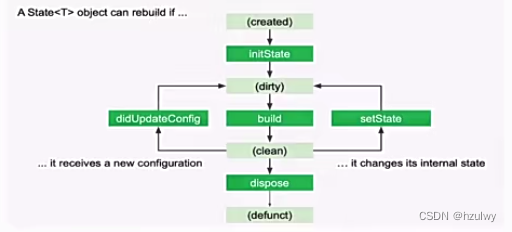
Flutter框架和原理剖析
Flutter是Google推出并开源的跨平台开发框架,主打跨平台、高保真、高性能。开发者可以通过Dart语言开发Flutter应用,一套代码同时运行在ios和Android平台。不仅如此,flutter还支持web、桌面、嵌入应用的开发。flutter提供了丰富的组件、接口&…
如何修复msvcp140.dll文件,msvcp140.dll丢失的解决方法
在使用电脑的过程中,可能会遇到提示“msvcp140.dll丢失”的错误。这通常是由于某些程序或游戏在运行时需要调用msvcp140.dll文件,但由于某种原因(如病毒感染、误删等),该文件被删除或损坏,导致程序无法正常…
易点易动系统帮助制药企业提供智能化固定资产管理方案
制药企业作为大宗重资产行业,其生产车间内各种设备及仪器往往复杂、种类繁多、数量众多。高效管理这些固定资产对企业生产作业来说显得尤为重要。但是,传统手写账目或excel电子表格等管理模式已不能适应如今海量资产的管理需求。易点易动专业从事固定资产管理领域多年,通过自主…
【学习笔记】各类基于决策单调性的dp优化
文章目录 对于决策单调性的一般解释关于决策单调性的证明四边形不等式一维dp区间dp一种二维dp一些满足四边形不等式的函数类 与图形相结合 决策单调性的常见优化手段二分队列二分栈分治类莫队做法 SMAWKWQS二分WQS多解情况满足四边形不等式的序列划分问题的答案凸性以及WQS二分…
机器学习笔记之无约束优化问题——(阶段性收尾)共轭方向法与Wolfe准则优化方法Python示例
机器学习笔记之无约束优化问题——基于共轭方向法与Wolfe准则优化方法的Python示例 引言小插曲:画图——非标准二次型的等值线算法在图像中的表示基于精确搜索的共轭梯度法基于Wolfe准则的共轭梯度法 附:共轭梯度法完整代码 引言
本节使用 Python \text…
EDA(Exploratory Data Analysis)探索性数据分析
EDA(Exploratory Data Analysis)中文名称为探索性数据分析,是为了在特征工程或模型开发之前对数据有个基本的了解。数据类型通常分为两类:连续类型和离散类型,特征类型不同,我们探索的内容也不同。
1. 特征类型
1.1 连续型特征 …
气膜体育馆内气压会对人体造成影响吗?
现如今,伴随着全民健身运动风潮的盛行,气膜体育馆的出现可谓是深受大众喜爱,气膜体育馆可以为我们提供更实用、更经济、更快速的体育场馆解决方案,帮助中国快速填补体育场馆不足的缺口,从而促进了全民的运动参与度和活…
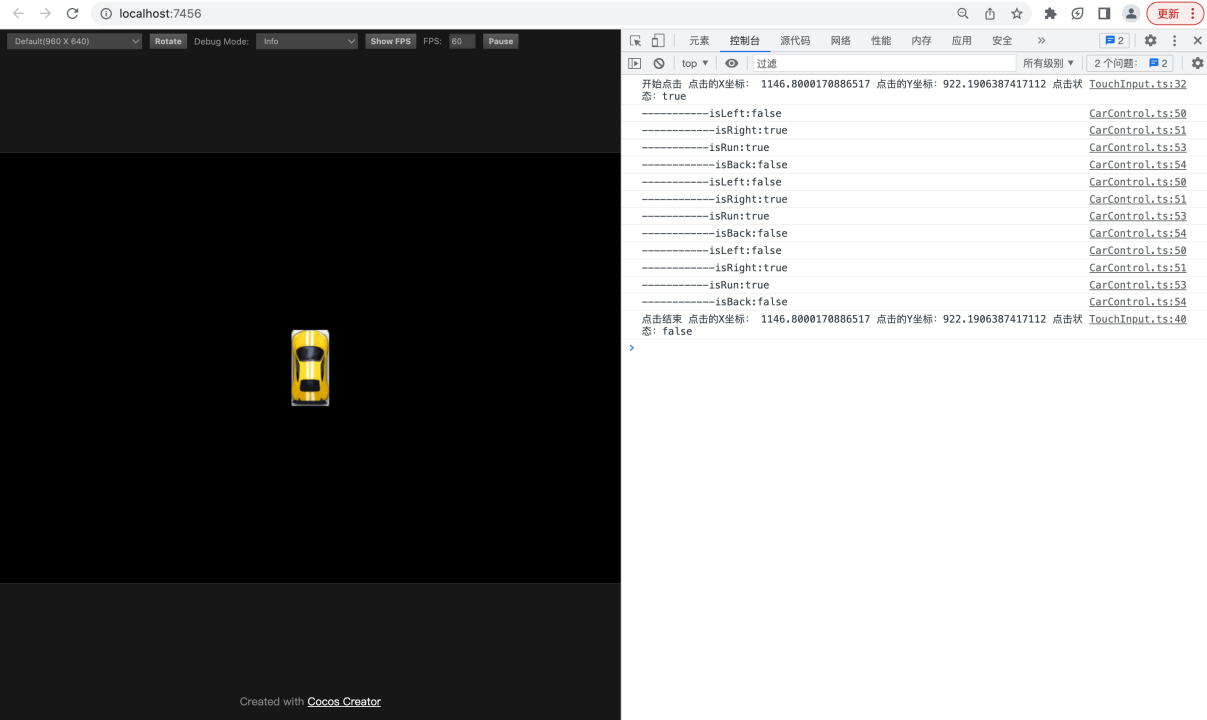
【基于Cocos Creator实现的赛车游戏】9.实现汽车节点的控制逻辑
转载知识星球 | 深度连接铁杆粉丝,运营高品质社群,知识变现的工具
项目地址:赛车小游戏-基于Cocos Creator 3.5版本实现: 课程的源码,基于Cocos Creator 3.5版本实现
在上一节的课程中,您已经实现了通过触控给刚体施…
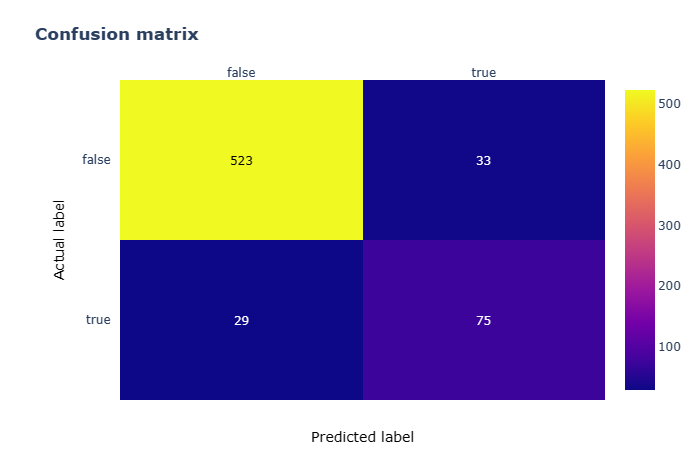
混淆矩阵和数据不平衡 (3/3)
一、说明 如果数据集数据不平恒,如何评估分类器的效果?如果分类器不好,如何改进分类器?本篇将讲述不平衡数据下,混淆矩阵的应用。在这里,我们将了解不同的指标,使用它们来解释从我们在上一练习中…
malloc与free
目录
前提须知:
malloc:
大意:
头文件:
申请空间:
判断是否申请成功:
使用空间: 结果:
整体代码: malloc申请的空间怎么回收呢?
注意事项:
free:…
【IntelliJ IDEA】cmd和idea Terminal查看java版本不一致
问题描述
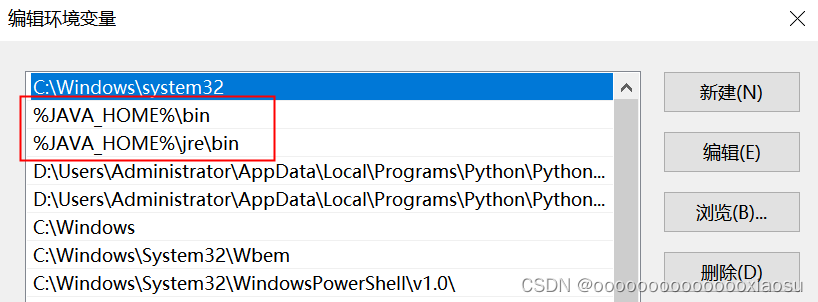
原来win10电脑上安装的是jdk8的版本,因某些原因,现在想换成jdk7的版本,修改环境变量后,在cmd中执行 [java -version]命令,显示的是7的版本。 但在idea的Terminal中执行,确实显示8的版本。
原因分…
tokenizers总结
简介
tokenize的目标是把输入的文本流,切分成一个个子串,每个子串相对有完整的语义,便于学习embedding表达和后续模型的使用。
tokenize有三种粒度:word/subword/char
word词,是最自然的语言单元。对于英文等自然语…
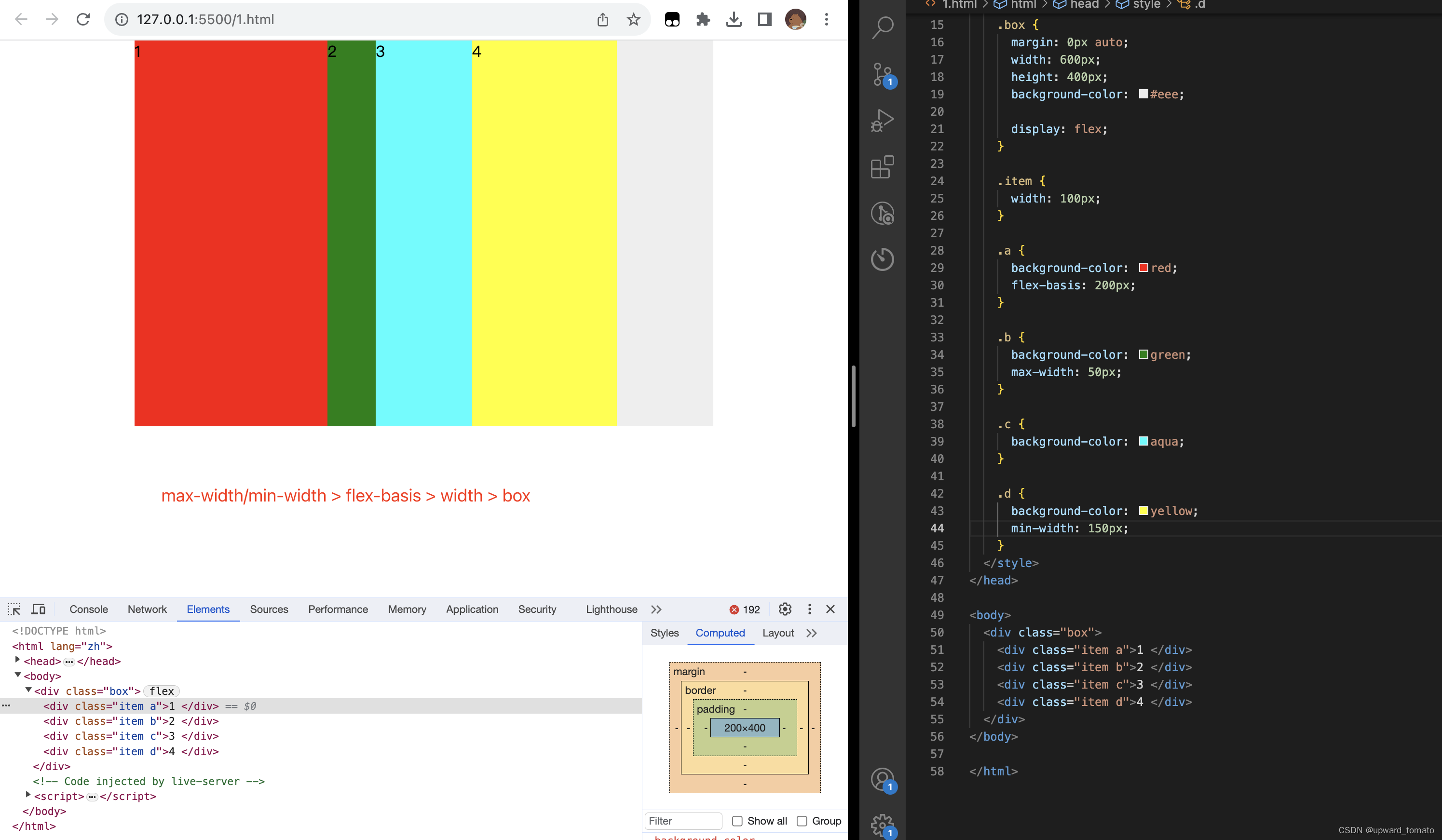
面试官:请说说flex布局_番茄出品.md
面试官:请说说flex布局_番茄出品.md
start
依然记得当初学习 flex 布局时,用 flex 布局:画麻将。一筒到九筒,应有尽有。但是光和面试官说,我用 flex 布局画过麻将,并没有什么用。面试官问你一个语法&…
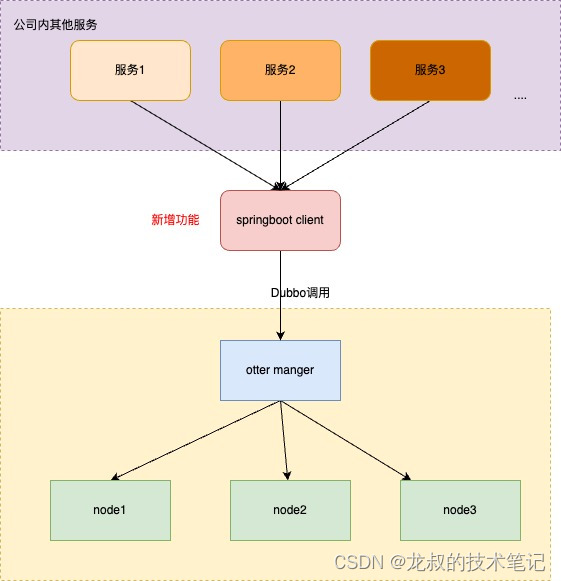
Otter改造 增加springboot模块和HTTP调用功能
环境搭建 & 打包
环境搭建:
进入 $otter_home/lib 目录执行:bash install.sh
打包:
进入$otter_home目录执行:mvn clean install -Dmaven.test.skip -Denvrelease发布包位置:$otter_home/target
项目背景 阿里…
Shiro 整合 Web
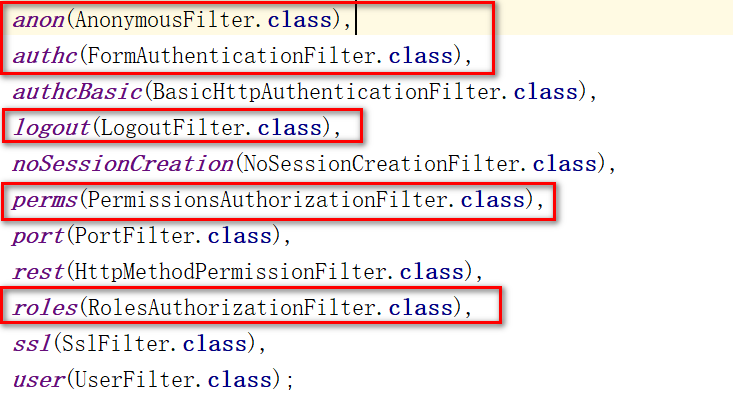
文章目录 Shiro的Web流程Shiro整合SSMShiro整合SpringBootShiro授权方式过滤器链自定义过滤器注解记住我 Shiro的Web流程 Shiro整合SSM
准备SSM的配置准备经典五张表(见Shiro基本使用),完成测试准备Shiro的配置 核心过滤器 <!-- 配置S…
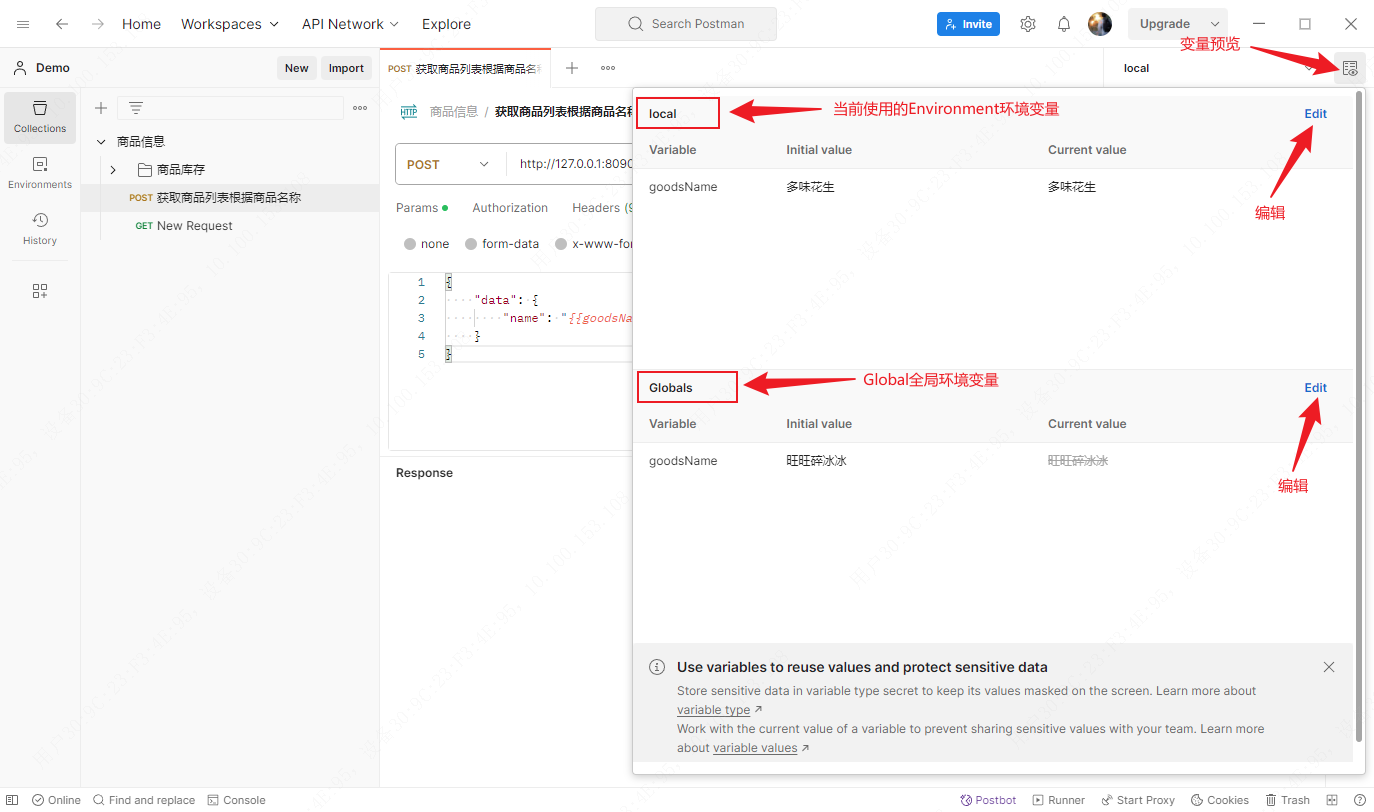
Postman应用——Variable变量设置(Global、Environment和Collection)
文章目录 Global变量设置Environment变量设置Collection变量设置Global、Environment环境变量预览 Global、Environment和Collection变量使用,点击查看。 Global变量设置
全局变量设置,作用域是所有Collection、Folder和Request,全局变量只有…
Leetcode每日一题:打家劫舍系列Ⅰ、Ⅱ、Ⅲ、Ⅳ(2023.9.16~2023.9.19 C++)
由于之前写过打家劫舍系列,这里直接弄个合集,后面应该还有个iv。
目录
198. 打家劫舍
213. 打家劫舍 II
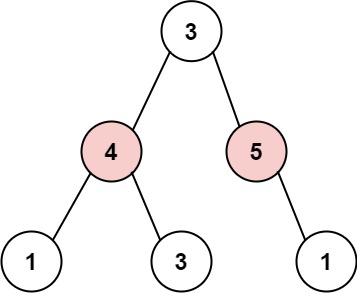
337. 打家劫舍 III
2560. 打家劫舍 IV 198. 打家劫舍
题目描述: 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都…
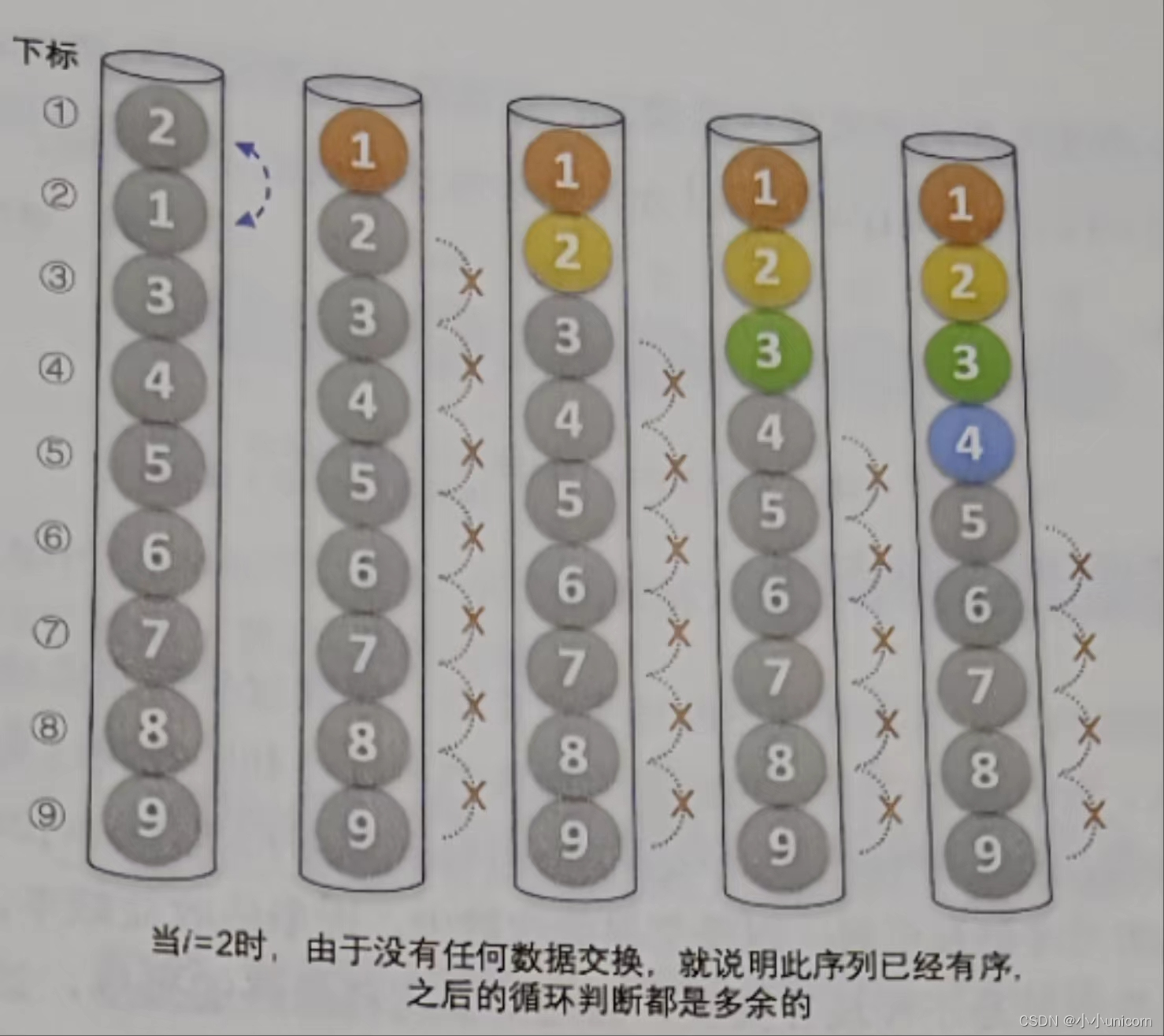
八大排序(二)--------冒泡排序
本专栏内容为:八大排序汇总 通过本专栏的深入学习,你可以了解并掌握八大排序以及相关的排序算法。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:八大排序汇总 🚚代码仓库:小小unicorn的代码仓库…
PDF怎么转图片?四种转换方法分享
PDF文件是一种非常常见的文档格式,然而,有时候我们需要将PDF文件转换成图片格式。比如我们可能需要将PDF文件中的某些页面或图表转换成图片格式以便于编辑或分享。在这篇文章中,我们将介绍四种将PDF文件转换成图片的方法。 方法一:…