本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.ldbm.cn/p/125915.html
如若内容造成侵权/违法违规/事实不符，请联系编程新知网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
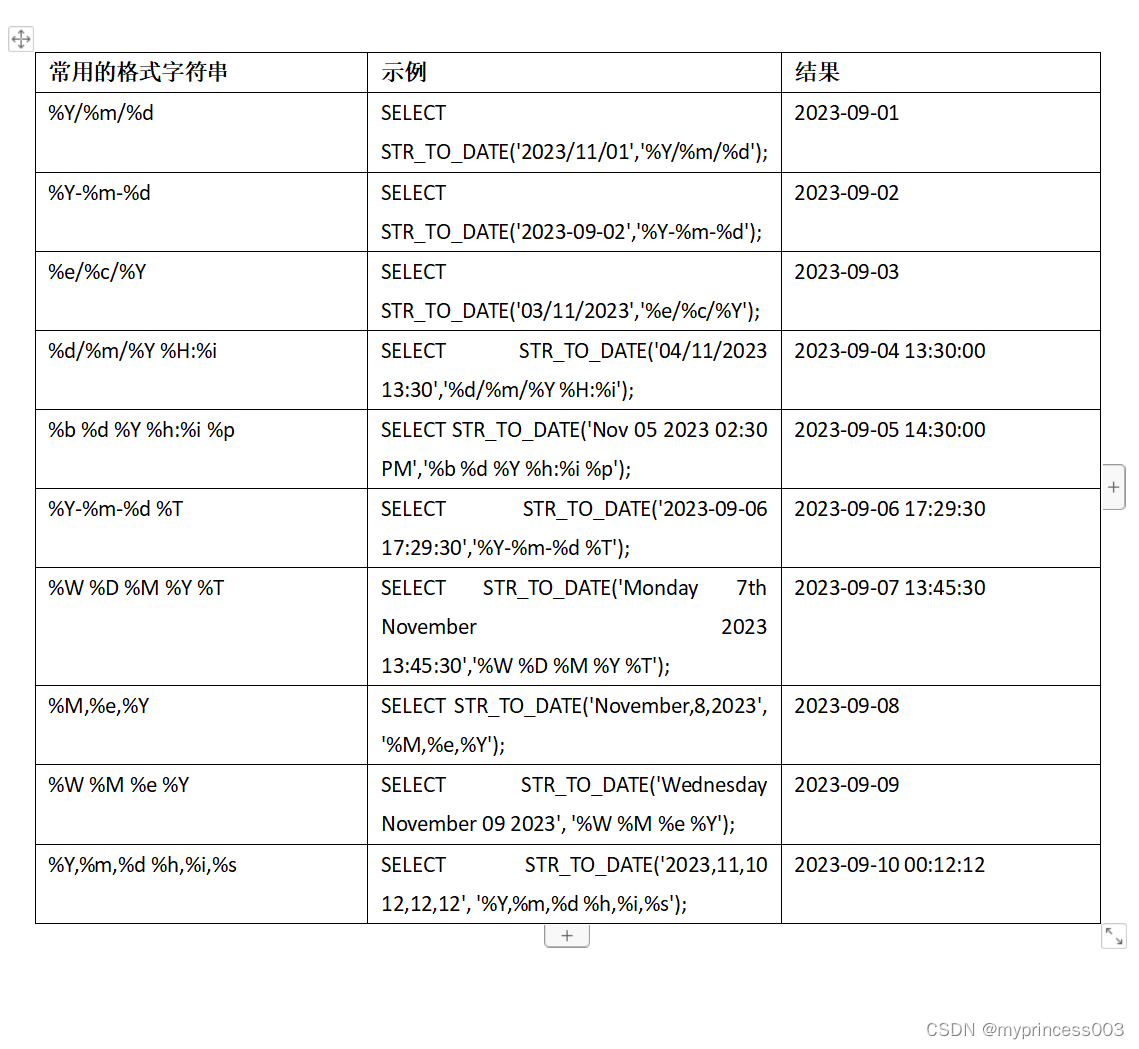
MySQL的时间差函数、日期转换计算函数
MySQL的时间差函数(TIMESTAMPDIFF、DATEDIFF)、日期转换计算函数(date_add、day、date_format、str_to_date)
时间差函数（TIMESTAMPDIFF、DATEDIFF）
需要用MySQL计算时间差，使用TIMESTAMPDIFF、DATEDIFF，记录一下实验结果
--0
…
大模型训练之加速篇 -attention优化【MQA-＞ flashAttention】
MQA (multi query attention)
Fast Transformer Decoding: One Write-Head is All You Need MQA 是 19 年提出的一种新的 Attention 机制，其能够在保证模型效果的同时加快 decoder 生成 token 的速度。 那到底能提升多少的速度呢，我们来看论文中给出的结…
OpenCV（三十八）：二维码检测
1.二维码识别原理
功能图形： 位置探测图形：通常，二维码中有三个位置探测图形，呈现L型或大角度十字架形状，分布在二维码的三个角上，用于帮助扫描设备定位二维码的位置和方向。 位置探测图形分隔符…
PoE交换机出现不稳定的原因有哪些？
带有供电设备的PoE交换机给使用者带来了方便，因此被广泛应用。然而，很多使用商反映他们所使用的PoE交换机不稳定。那么，PoE交换机出现不稳定的原因有哪些？ 首先需要考虑的是数据传输的距离。尽管PoE供电交换机具有方便灵活的特点&…
leetcode646. 最长数对链(java)
最长数对链 题目描述贪心解法二 动态规划 dp 题目描述 难度 - 中等 leetcode646. 最长数对链(java) 给你一个由 n 个数对组成的数对数组 pairs ，其中 pairs[i] [lefti, righti] 且 lefti < righti 。 现在，我们定义一种 跟随 关系，当且仅…
使用扩展运算符（...）合并数组
在项目开发过程中，有一个需求，需要制作一个带有标题的表格，如下所示： 和后端开发沟通时，后端计划返回三个数组，标题写死。所以我需要做的就是把数组合并，然后在三个数组之前增加标题。这里我采用…
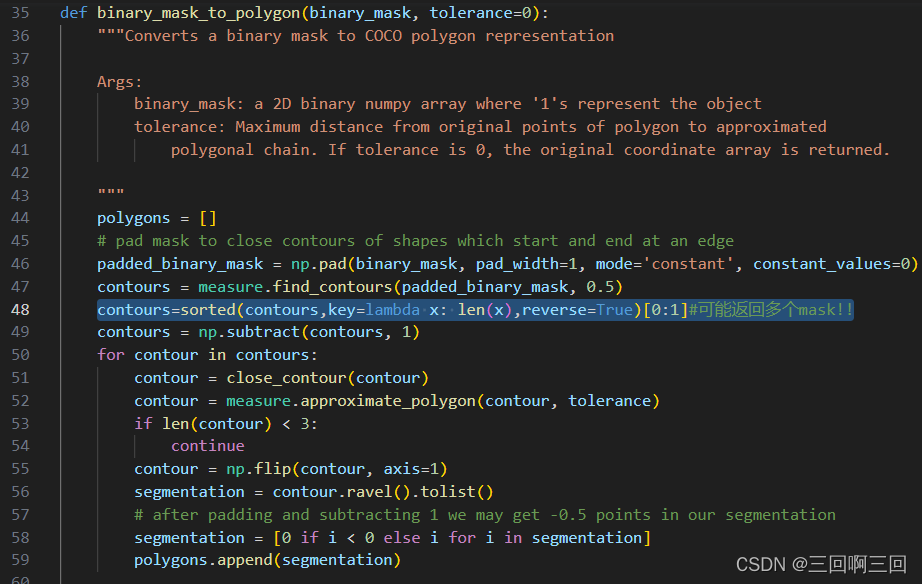
解决pycococreatortools安装问题
我的环境：
python:3.8.18
numpy:1.24.4
问题一：
用git文档的方法下载失败：
pip install gitgit://github.com/waspinator/coco.git2.1.0 解决：
用这行 pip install githttps://github.com/waspinator/pycococreator.git 问题…
DBAPI插件开发指南
DBAPI插件开发指南
插件市场
您可以去插件市场下载插件
插件的作用
DBAPI的插件分4类，分别是数据转换插件、缓存插件、告警插件、全局数据转化插件
缓存插件
对执行器结果进行缓存，比如SQL执行器，对查询类SQL，sql查询结果进…
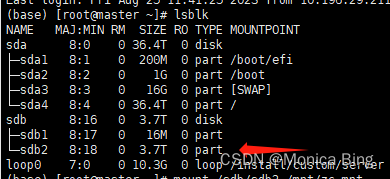
linux挂载ntfs格式硬盘
先把硬盘连接到服务器上 如果没有安装ntfs-3g软件的话 sudo apt-get install ntfs-3g查看ntfs分区并找到要挂载的NTFS分区的设备名 lsblk这里我是根据SIZE找到的设备名 也可以挂载之前先查看一下，挂载之后再看新增了哪个分区，就可以定位到啦 开始mnt 先…
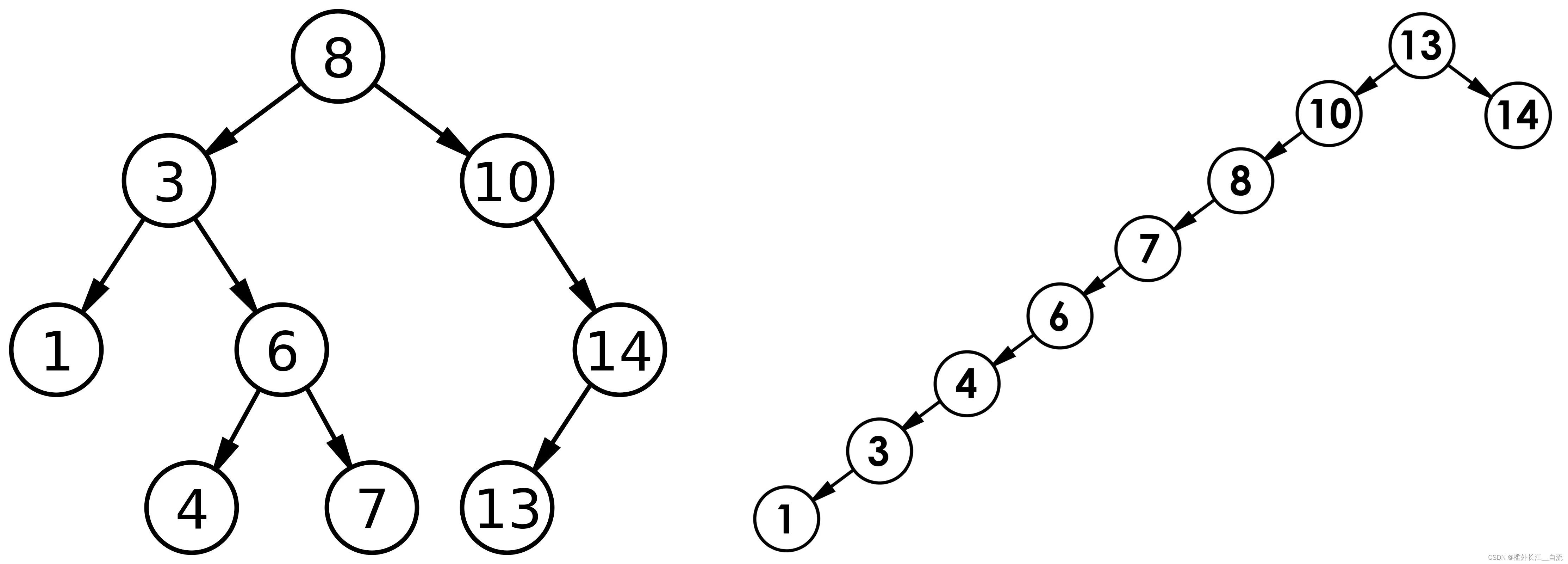
二叉搜索树（BST，Binary Search Tree）
文章目录 1. 二叉搜索树1.1 二叉搜索树概念1.2 二叉搜索树的查找1.3 二叉搜索树的插入1.4 二叉搜索树的删除 2 二叉搜索树的实现3 二叉搜索树的应用3.1二叉搜索树的性能分析 1. 二叉搜索树
1.1 二叉搜索树概念
二叉搜索树又称二叉排序树，它或者是一棵空树…
python处理CSV文件
CSV库还有其他处理CSV的方法，这里只是介绍几个常用的，后面如果用到别的会进行更新
目录
1 生成一个新的csv文件，并向其中写一点东西
2 单纯往里面写几行 3 读取csv文件 1 生成一个新的csv文件，并向其中写一点东西
import…
Pytorch-MLP-Mnist
文章目录 model.pymain.py参数设置注意事项初始化权重如果发现loss和acc不变关于数据下载关于输出格式 运行图 model.py
import torch.nn as nn
import torch.nn.functional as F
import torch.nn.init as initclass MLP_cls(nn.Module):def __init__(self,in_dim28*28):super…
Java实现添加文字水印、图片水印功能实战
Java实现添加文字水印、图片水印功能实战
本文介绍java实现在图片上加文字水印的方法，水印可以是图片或者文字，操作方便。
java实现给图片添加水印实现步骤：
获取原图片对象信息（本地图片或网络图片）添加水印&#…
【数字通信原理】第三章—信源编码理论
文章目录 第三章 信源编码理论1.模拟信号的数字化概论2. 信源编码的基本原理2.1 抽样定理2.1.1 低通抽样定理2.1.2 带通抽样定理 2.2 脉冲振幅调制PAM2.2.1 自然抽样2.2.2 平顶抽样 第三章 信源编码理论
1.模拟信号的数字化概论 2. 信源编码的基本原理
2.1 抽样定理
2.1.1 低…
使用Python构建强大的网络爬虫
介绍 网络爬虫是从网站收集数据的强大技术，而Python是这项任务中最流行的语言之一。然而，构建一个强大的网络爬虫不仅仅涉及到获取网页并解析其HTML。在本文中，我们将为您介绍创建一个网络爬虫的过程，这个爬虫不仅可以获取和保存网…
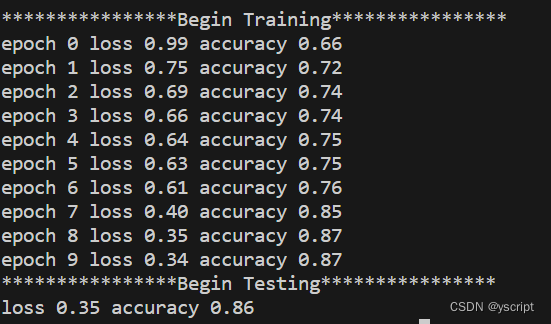
![计算机视觉与深度学习-全连接神经网络-训练过程-欠拟合、过拟合和Dropout- [北邮鲁鹏]](https://img-blog.csdnimg.cn/335ba2d4b4b3432fb8863d88060031ef.png)
计算机视觉与深度学习-全连接神经网络-训练过程-欠拟合、过拟合和Dropout- [北邮鲁鹏]
目录标题 机器学习的根本问题过拟合overfitting泛化能力差。应对过拟合最优方案次优方案调节模型大小约束模型权重，即权重正则化(常用的有L1、L2正则化)L1 正则化L2 正则化对异常值的敏感性随机失活(Dropout)随机失活的问题 欠拟合 机器学习的根本问题 机器学习的根…
![[Hadoop] start-dfs.sh ssh报错](https://img-blog.csdnimg.cn/a2b48d2c570447caab9cbb723814c886.png)
[Hadoop] start-dfs.sh ssh报错
Permission denied (publickey
决解方案
相关命令
cd ~/.sshssh-keygen -t rsa -p""cat id_rsa.pub >> authorized_keyschmod 0600 authorized_keys
相关链接Hadoop: start-dfs.sh permission denied - Stack Overflow Java HotSpot(TM) Server VM warning…
在线旅游平台步入新时代，携程如何走出自己的路？
今年旅游从线下到线上全方位火了。有统计数据，一季度，光是抖音，旅游达人发布视频数量就高达175万条，播放量1350亿次，收获27亿次点赞。在这一趋势下，许多“不出名”的景区和酒店借势抖音达人完成“出圈”。短…