本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.ldbm.cn/p/144548.html
如若内容造成侵权/违法违规/事实不符，请联系编程新知网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
Sublime Text 4 for Mac激活下载
Sublime Text for Mac是一款适用于Mac平台的文本编辑器。它具有快速的性能和丰富的功能，可以帮助用户快速进行代码编写和文本编辑。 软件下载：Sublime Text 4 for Mac激活下载 该软件具有直观的界面和强大的功能，包括多行选择、代码折叠、自动…
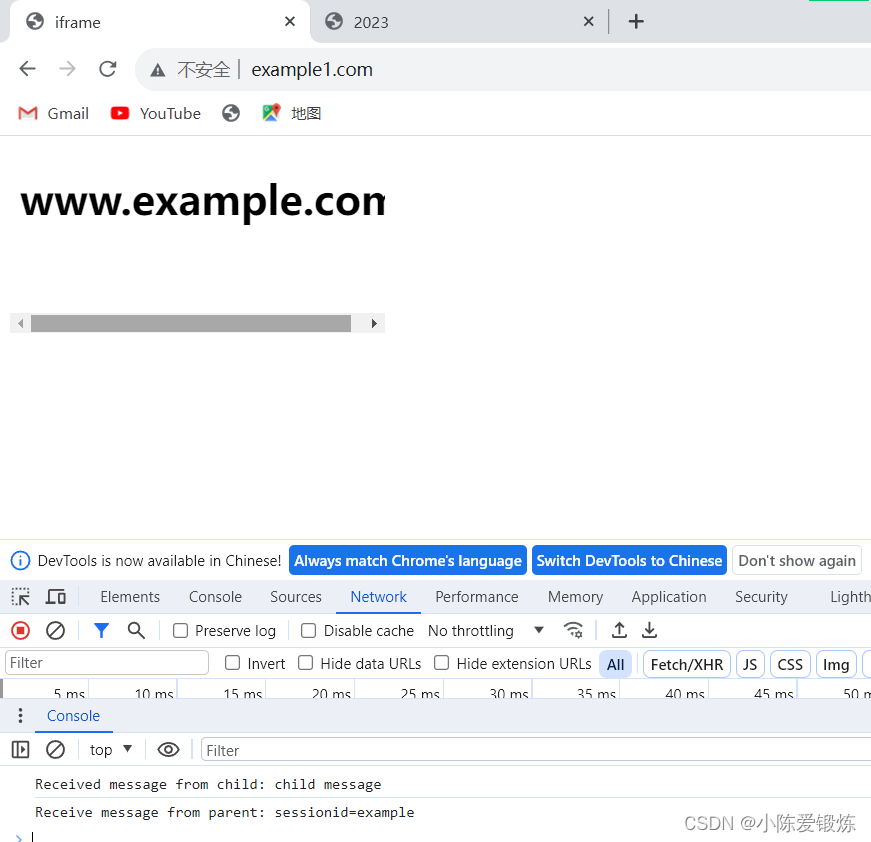
正则验证用户名和跨域postmessage
正则验证用户名 字母数字符号大小写8-14匹配用户名的
<!DOCTYPE html>
<html>
<head><meta charset"utf-8"><meta name"viewport" content"widthdevice-width, initial-scale1"><title>form</title>
…
行与走，放慢自己，思考回顾。
为什么要出去行与走？
1、出去行与走看到祖国的大美风景，可以更深刻的认识到我们祖国的美好。
2、可以放空心情，排除掉积攒在写字楼内的方格子里面的郁闷和烦恼。
3、可以为自己的身体和心灵找一个安静和清澈净土。
4、在行和走之间&#…
【C++ 学习 ㉕】- 万字详解 unordered_map 和 unordered_set（哈希表的查找和容器的模拟实现）
目录
一、unordered_map 的基本介绍
二、unordered_set 的基本介绍
三、相关练习
3.1 - 在长度 2N 的数组中找出重复 N 次的元素
3.2 - 存在重复元素
3.3 - 两句话中的不常见单词
四、哈希表的查找
4.1 - 哈希表的基本概念
4.2 - 哈希函数的构造方法
4.3 - 处理冲突的…
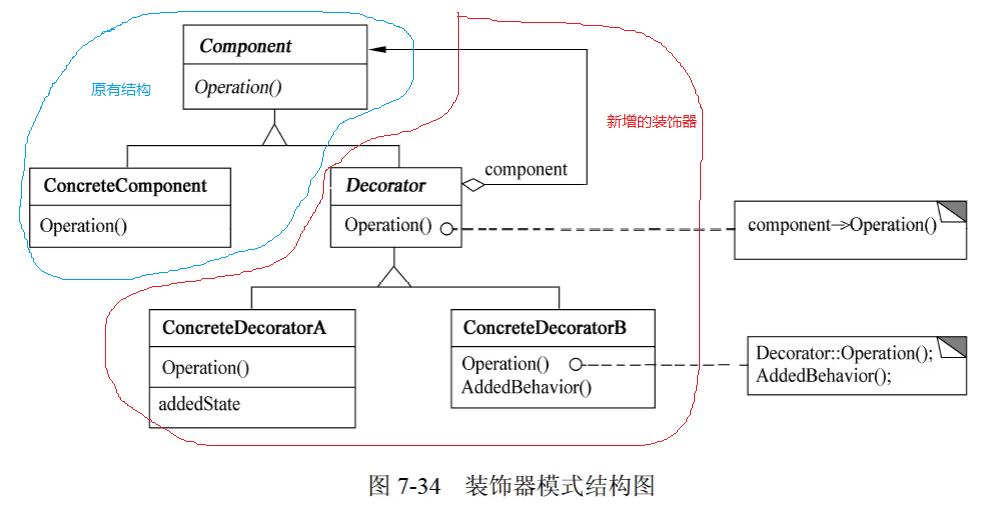
设计模式——Decorator(装饰器模式)
Decorator(装饰器模式)
目的：
动态地给一个对象添加一些额外的职责。
适用性：
在不影响其他对象的情况下，以动态、透明的方式给单个对象添加职责。
简单解释
当有一个已经完成的系统，其中类和对象的关系的错综复杂的&#x…
力扣 -- 1027. 最长等差数列
解题步骤： 参考代码：
class Solution {
public:int longestArithSeqLength(vector<int>& nums) {int nnums.size();int ret2;unordered_map<int,int> hash;//这里可以先把nums[0]存进哈希表中，方便后面i从1开始遍历hash[num…
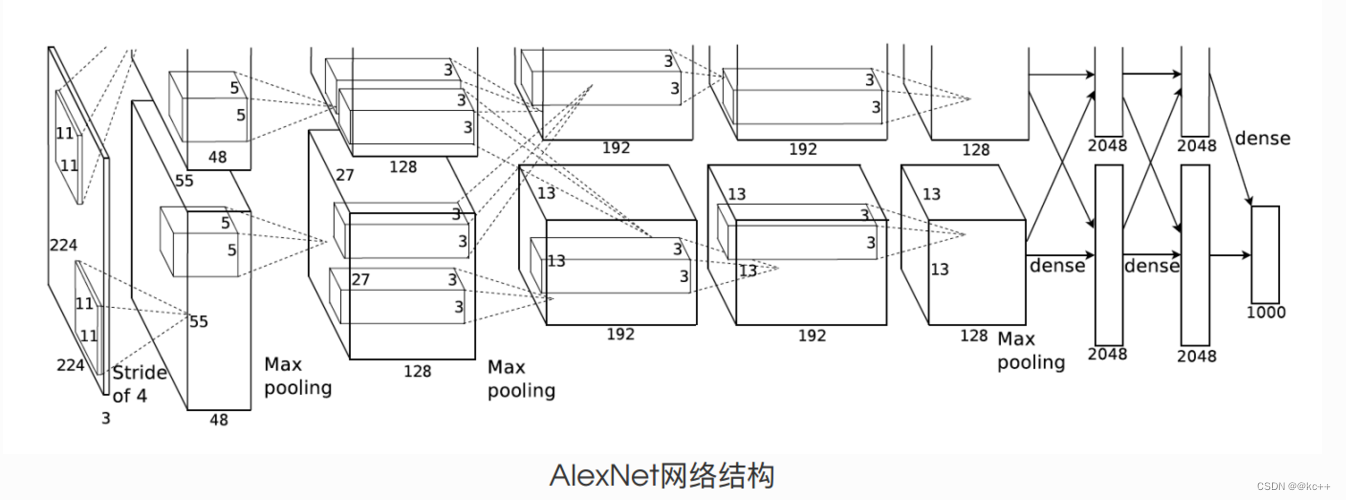
AlexNet网络复现
1. 引言
在现代计算机视觉领域，深度学习已经成为了一个核心技术，其影响力远超过了传统的图像处理方法。但深度学习，特别是卷积神经网络（CNN）在计算机视觉的主导地位并不是从一开始就有的。在2012年之前，计…
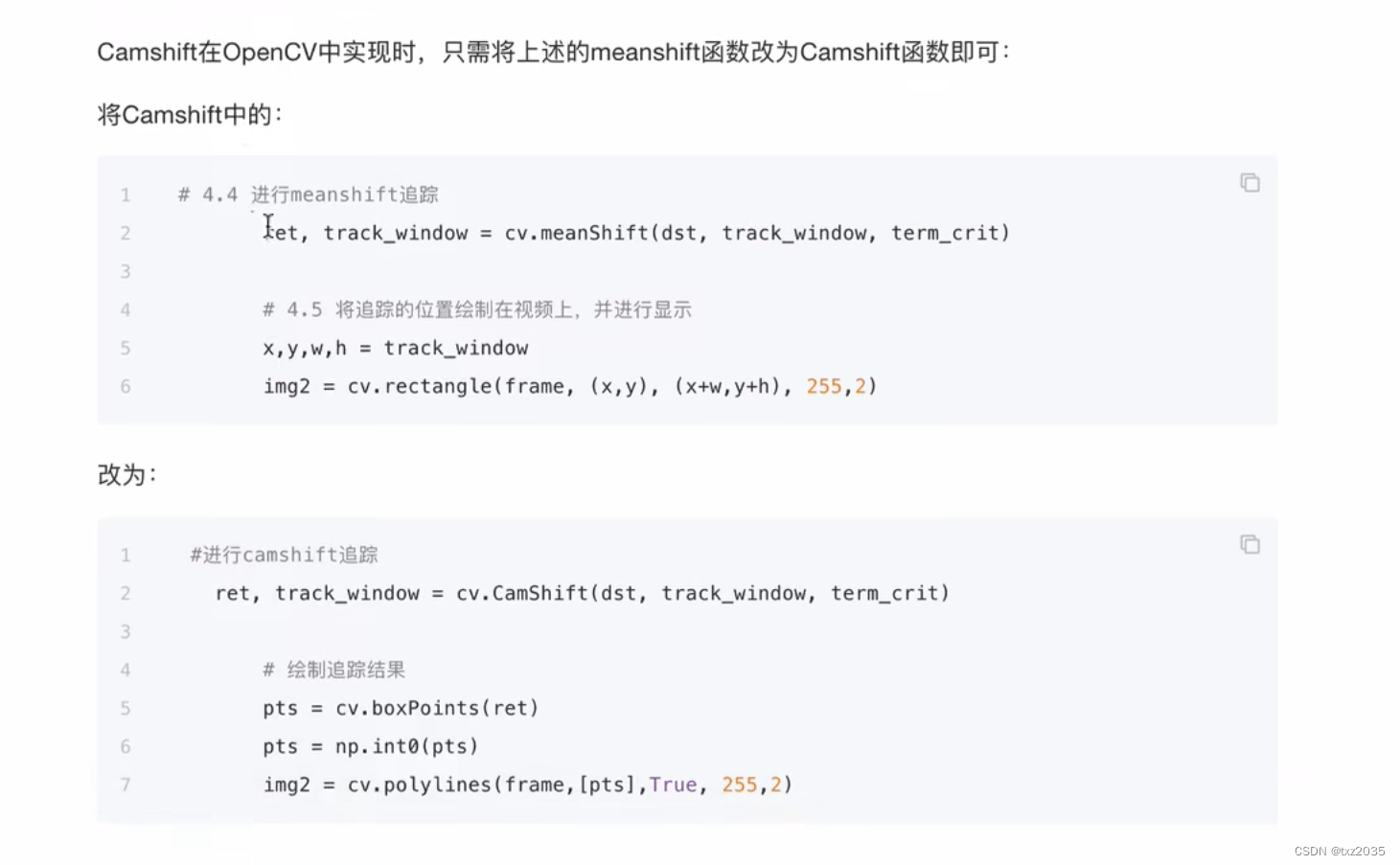
OpenCV利用Camshift实现目标追踪
目录 原理
做法
代码实现
结果展示 原理 做法 代码实现
import numpy as np
import cv2 as cv# 读取视频
cap cv.VideoCapture(video.mp4)# 检查视频是否成功打开
if not cap.isOpened():print("Error: Cannot open video file.")exit()# 获取第一帧图像&#x…
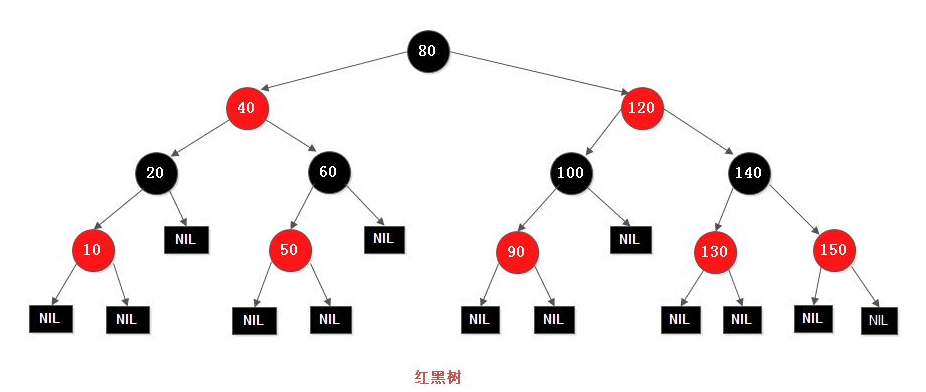
【简单了解一下红黑树】
文章目录 红黑树1.简介2.为什么需要红黑树？3.性质4. 红黑树的效率4.1 红黑树效率4.2 红黑树和AVL树的比较 5.AVL树 vs 红黑树5.1 AVL树5.2 红黑树5.3 如何选择 红黑树 1.简介
红黑树是一种自平衡的二叉查找树，是一种高效的查找树。它是由 Rudolf Bayer …
Nature Machine Intelligence | “化学元素知识+功能提示”双驱动，探索分子预测新方法
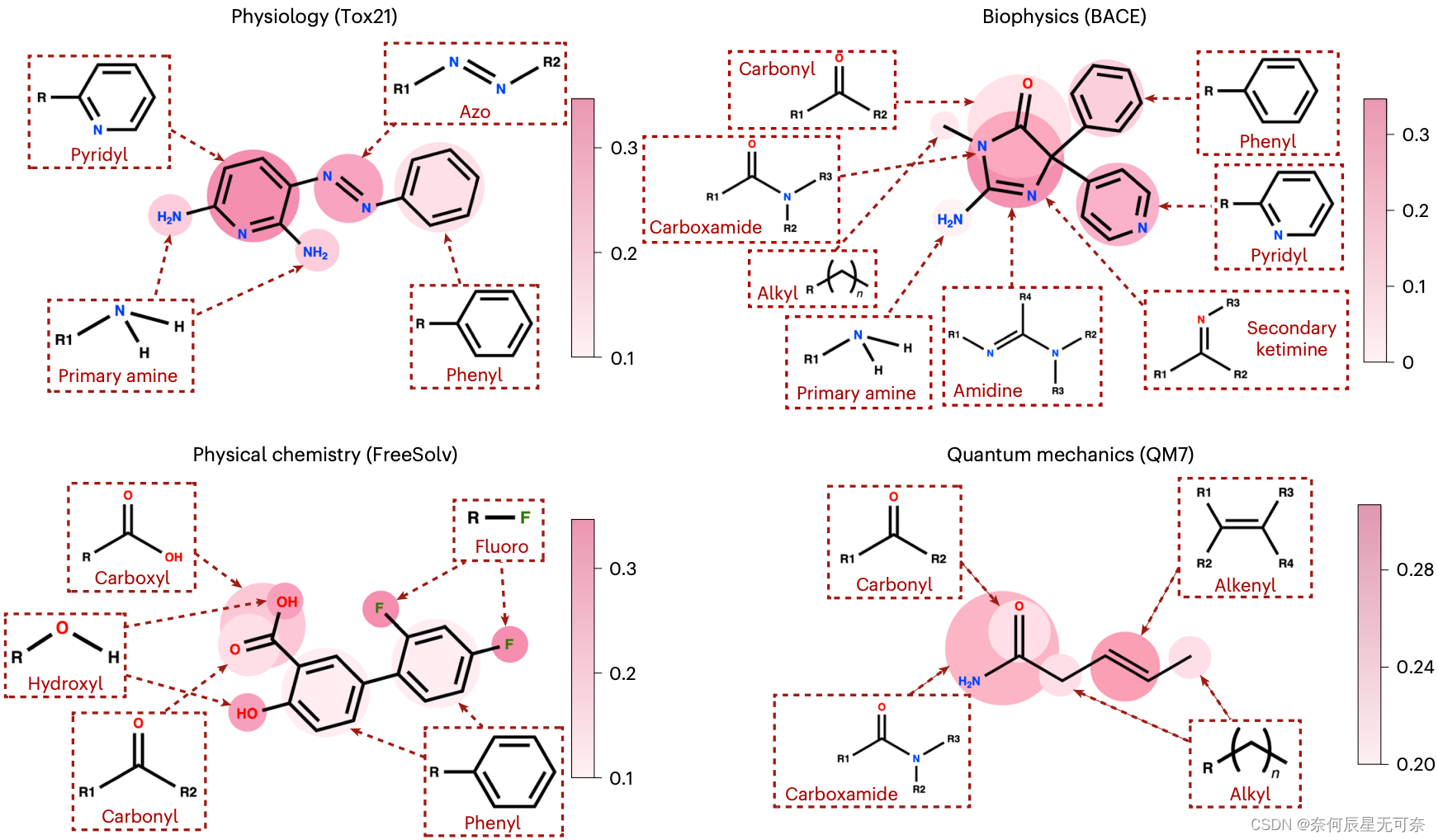
论文题目：Knowledge graph-enhanced molecular contrastive learning with functional prompt 论文链接：https://doi.org/10.1038/s42256-023-00654-0 项目地址：GitHub - HICAI-ZJU/KANO: Code and data for the Nature Machine Intelligence…
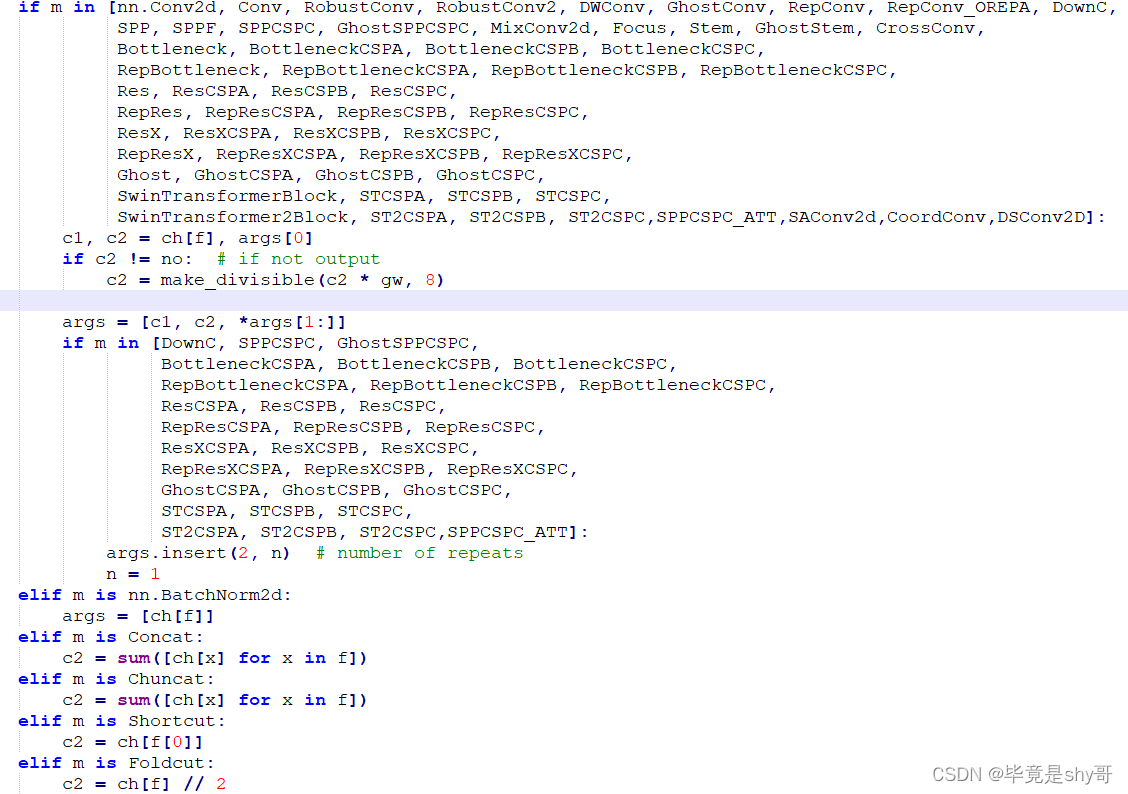
yolo如何添加模块？？？修改parse_model（）
如何修改添加模块！！！ 先贴代码，加模块时有些地方需要修改，只讲核心部分！！！！
def parse_model(d, ch): # model_dict, input_channels(3)logger.info(\n%3s%18s%3s%10s …
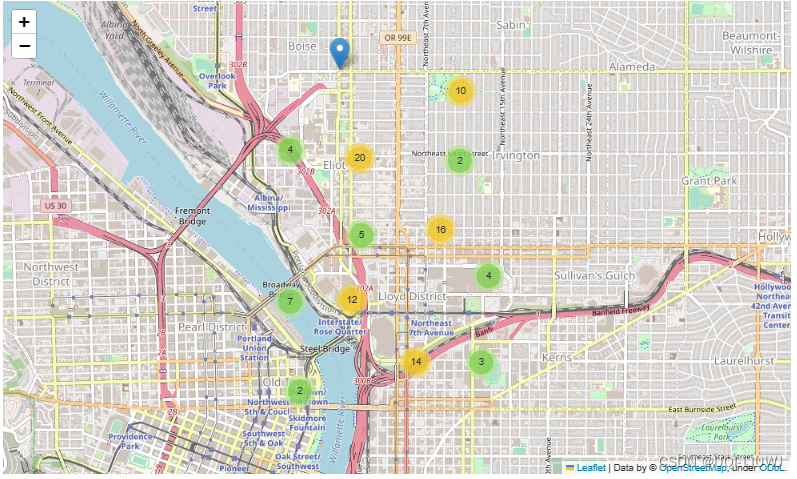
Folium 笔记：MarkerCluster
在一张地图上以聚簇的形式显示大量的标记（markers）
举例：
import folium
from folium.plugins import MarkerCluster
import randomm folium.Map(location[45.5236, -122.6750], zoom_start13)
# 创建一个基本的地图marker_cluster Marker…
14链表-环形链表、龟兔赛跑算法
目录
LeetCode之路——141. 环形链表
分析：
解法一：哈希表
解法二：龟兔赛跑 LeetCode之路——141. 环形链表
给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针…
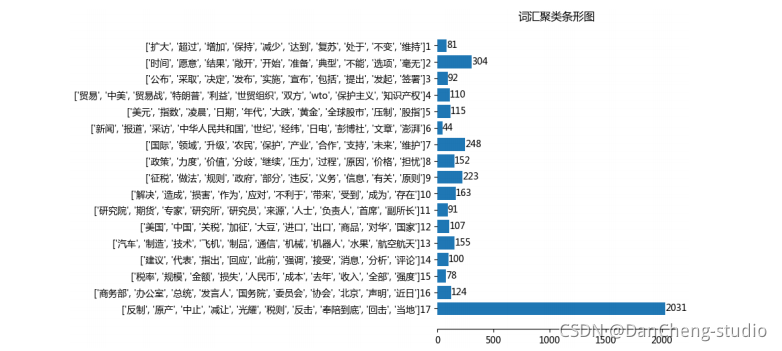
计算机竞赛 题目：基于FP-Growth的新闻挖掘算法系统的设计与实现
文章目录 0 前言1 项目背景2 算法架构3 FP-Growth算法原理3.1 FP树3.2 算法过程3.3 算法实现3.3.1 构建FP树 3.4 从FP树中挖掘频繁项集 4 系统设计展示5 最后 0 前言
🔥 优质竞赛项目系列，今天要分享的是
基于FP-Growth的新闻挖掘算法系统的设计与实现…
项目进展（三）-电机驱动起来了，发现了很多关键点，也遇到了一些低级错误，
一、前言
昨天电机没有驱动起来，头发掉一堆，不过今天，终于终于终于把电机驱动起来了！！！！，特别开心，哈哈哈哈，后续继续努力完善！！&…
![[Machine Learning]pytorch手搓一个神经网络模型](https://img-blog.csdnimg.cn/10a66ad06f04418b984833e59194d5e5.png)
[Machine Learning]pytorch手搓一个神经网络模型
因为之前虽然写过一点点关于pytorch的东西，但是用的还是他太少了。
这次从头开始，尝试着搓出一个神经网络模型
（因为没有什么训练数据，所以最后的训练部分使用可能不太好跑起来的代码作为演示，如果有需要自己连上数据…
OOTD | 美式复古穿搭耳机，复古轻便的头戴式耳机推荐
复古耳机更能带来年代感的复古数码产品，头戴式耳机就好似是时光滤镜的时髦配饰，不说功能实用性，在造型上添加就很酷。
随着时代的发展，时尚有了新的定义。对如今的消费者来说，时尚不仅是美学与个性的展现，…