本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.ldbm.cn/p/208104.html
如若内容造成侵权/违法违规/事实不符，请联系编程新知网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
iphone15 nplayer播放本地电影投屏天猫魔盒(电视)卡顿解决方案
文章目录 投屏环境现象写在前面 解决方案所需投屏app安装方法试用结果如果文章对您有用，欢迎收藏或关注！ iphone15 nplayer播放本地电影投屏天猫魔盒(电视)卡顿解决方案 投屏环境
全千兆wifi6局域网 1000兆电信宽带 天猫魔盒4Pro 8G（M19&…
【RabbitMQ】RabbitMQ 消息的堆积问题 —— 使用惰性队列解决消息的堆积问题
文章目录 一、消息的堆积问题1.1 什么是消息的堆积问题1.2 消息堆积的解决思路 二、惰性队列解决消息堆积问题2.1 惰性队列和普通队列的区别2.2 惰性队列的声明方式2.3 演示惰性队列接收大量消息2.4 惰性队列的优缺点 一、消息的堆积问题
1.1 什么是消息的堆积问题
消息的堆积…
基于 VTable 的多维数据展示的原理与实践
多维表格介绍
多维表格又名透视表、交叉表、Pivot Table，指的是可以在行维度和列维度放入一个或多个维度，显示维度之间相互关系的一种表格。用户可以一目了然地分析出各种场景指标以及对比，旨在帮助业务分析推动决策。
假设需要分析如下表格…
自动驾驶行业观察之2023上海车展-----车企发展趋势(3)
合资\外资发展 宝马：i7、iX1新车亮相，未来将持续发力电动化、数字化（座舱）
宝马在本次车展重点展示了电动化产品，新发车型为i7 M70L、iX1、及i vision Dee概念车等车型。
• 展示重点：电动化数字化&#…
01-Spring中事务的实现之编程式事务和声明式事务,以及事务的属性之传播行为,隔离级别,事务的回滚
银行账户转账异常
需求: 实现act-001账户向act-002账户转账10000,要求两个账户的余额一个减成功一个加成功,即执行的两条update语句必须同时成功或失败
实现步骤
第一步: 引入项目所需要的依赖
<?xml version"1.0" encoding"UTF-8"?>
<proj…
程序员用接单平台靠谱吗？浅谈一下十年程序员的看法
后疫情时代，经济下行，这年头社会上就业也越来越卷了，程序员人才市场也日趋饱和。不少人嗅到危险气息，已经开始谋求出路了!
咱们程序员的话，“兼职”"接单"也不是个新鲜的话题了。养家糊口也好、财富自由也罢…
【MongoDB】集群搭建实战 | 副本集 Replica-Set | 分片集群 Shard-Cluster | 安全认证
文章目录 MongoDB 集群架构副本集主节点选举原则搭建副本集主节点从节点仲裁节点 连接节点添加副本从节点添加仲裁者节点删除节点 副本集读写操作副本集中的方法 分片集群分片集群架构目标第一个副本集第二个副本集配置集初始化副本集路由集添加分片开启分片集合分片删除分片 安…
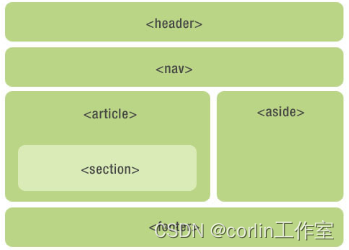
HTML5的语义元素
HTML5语义元素：
HTML5提供新的语义元素来明确一个web页面的不同部分：<head>、<nav>、<section>、<article>、<aside>、<figcation>、<figure>、<footer>。 1）、<section>元素&#x…
史上最全，从初级测试到高级测试开发面试题汇总，冲击大厂年50w+
目录：导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结（尾部小惊喜） 前言
接口测试面试相关…
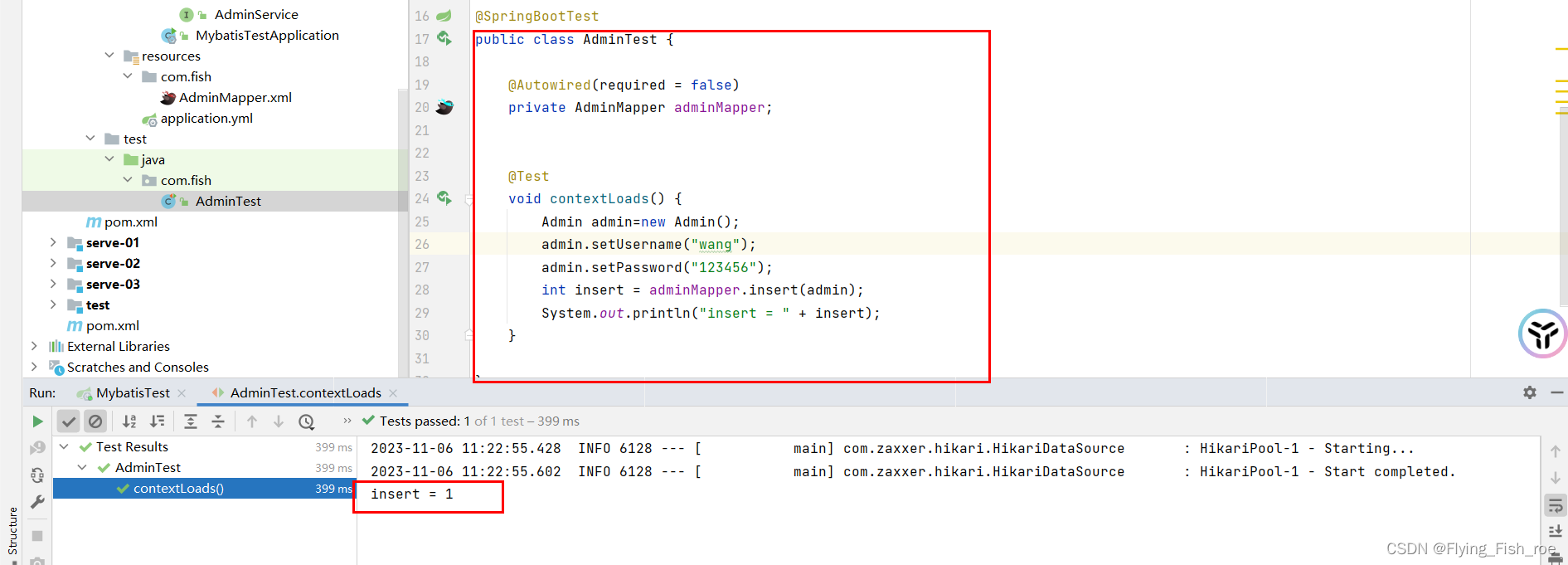
mybatis在springboot当中的使用
1.当使用Mybatis实现数据访问时，主要：
- 编写数据访问的抽象方法 - 配置抽象方法对应的SQL语句
关于抽象方法：
- 必须定义在某个接口中，这样的接口通常使用Mapper作为名称的后缀，例如AdminMapper - Mybatis框架底…
10 DETR 论文精读【论文精读】End-to-End Object Detection with Transformers
DETR 这篇论文，大家为什么喜欢它？为什么大家说它是一个目标检测里的里程碑式的工作？而且为什么说它是一个全新的架构？ 大家好，今天我们来讲一篇 ECC V20 的关于目标检测的论文。它的名字想必大家都不陌生，也…
![[移动通讯]【Carrier Aggregation-12】【LTE Carrier Aggregation basics 】](https://img-blog.csdnimg.cn/ac5ba0f652c646578170fac4d6f8d88d.png)
[移动通讯]【Carrier Aggregation-12】【LTE Carrier Aggregation basics 】
前言： 参考： RF Wireless World： 《LTE Carrier Aggregation basics》
目录： Why Carrier Aggregation Carrier Aggregation in TDD LTE Carrier Aggregation in FDD LTE Carrier Aggregation frequency ba…
「图像 cv2.seamlessClone」无中生有制造数据
上一篇博客【「图像 merge」无中生有制造数据 】写的是图片直接融合，此方法生成的图片相对而言比较生硬，虽然目标图片已经透明化处理过了，但是生成的图片依旧很假 除了上述上述的图片叠加融合之外，还有一种更加自然的融合方法&…
ZKP16 Hardware Acceleration of ZKP
ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 16: Hardware Acceleration of ZKP (Guest Lecturer: Kelly Olson) The What and Why of Hardware Acceleration Hardware acceleration is the use of dedicated hardware to accelerate an operation so that it runs faster…
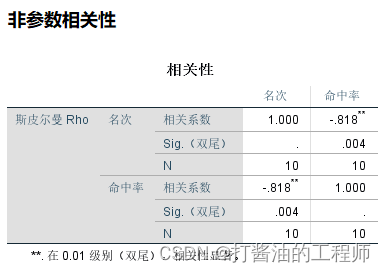
学习笔记|秩相关分析|Spearman相关分析|Kendall相关分析|规范表达|《小白爱上SPSS》课程：SPSS第十九讲：秩相关分析怎么做？
目录 学习目的软件版本原始文档秩相关分析一、实战案例二、统计策略三、SPSS操作四、结果解读五、规范表达1、规范图表2、规范文字 六、划重点： 学习目的
SPSS第十九讲：秩相关分析怎么做？
软件版本
IBM SPSS Statistics 26。
原始文档
《…
windows 11渗透测试工具箱
系统简介
本环境旨在提供一个开箱即用的windows渗透测试环境；建议运行环境：【vmware：17.0 】 /【运行内存：8G】 /【固态硬盘：100G】 Windows11 Penetration Suite Toolkit v2.2 (WSL) 【推荐】 下载链接：h…
关于iOS：如何使用SwiftUI调整图片大小？
How to resize Image with SwiftUI? 我在Assets.xcassets中拥有很大的形象。 如何使用SwiftUI调整图像大小以缩小图像？
我试图设置框架，但不起作用： 1 2 Image(room.thumbnailImage) .frame(width: 32.0, height: 32.0) 在Image上应用…
NOIP2000提高组第二轮T4：方格取数
题目链接
[NOIP2000 提高组] 方格取数
题目描述
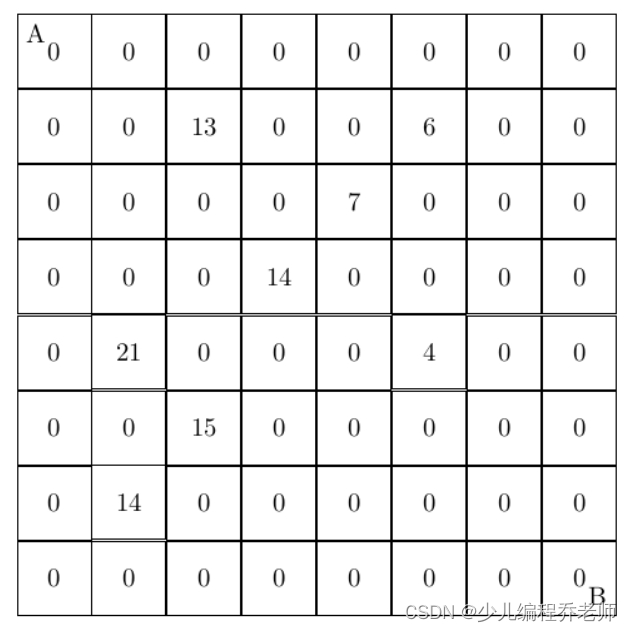
设有 N N N \times N NN 的方格图 ( N ≤ 9 ) (N \le 9) (N≤9)，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 0 0 0。如下图所示（见样例）:
某人从图的左上…