本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.ldbm.cn/p/228354.html
如若内容造成侵权/违法违规/事实不符，请联系编程新知网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
【C++ std::max_element std::min_element std::minmax_element】
一 、std::max_element 寻找范围 [first, last) 中的最大元素。 (1) 用 operator< 比较元素。 (3) 用给定的二元比较函数 comp 比较元素。 (2),(4) 同 (1,3) ，但按照 policy 执行。这些重载仅若 std::is_execution_policy_v<std::decay_t > (C20 前)std:…
bclinux aarch64 ceph 14.2.10 对象存储 http网关 CEPH OBJECT GATEWAY Civetweb
相关内容
bclinux aarch64 ceph 14.2.10 文件存储 Ceph File System, 需要部署mds： ceph-deploy mds-CSDN博客
ceph-deploy bclinux aarch64 ceph 14.2.10【3】vdbench fsd 文件系统测试-CSDN博客
ceph-deploy bclinux aarch64 ceph 14.2.10【2】vdbench rbd 块设…
AJAX入门Day01笔记
Day01_Ajax入门
知识点自测 如下对象取值的方式哪个正确? let obj {name: 黑马
}A: obj.a B: obj()a 答案 A选项正确 哪个赋值会让浏览器解析成标签显示? let ul document.querySelector(#ul)
let str <span>我是span标签</span>A: ul.innerText str B: ul…
计算机网络——物理层-编码与调制（数字基带信号、模拟基带信号、码元、常用编码、基本调制方法、混合调制）
目录
编码与调制
数字基带信号
模拟基带信号
码元
常用编码
不归零编码
归零编码
曼彻斯特编码
差分曼彻斯特编码
编码习题
基本调制方法
调幅
调频
调相
混合调制
QAM-16 编码与调制
在计算机网络中，计算机需要处理和传输用户的文字、图片、音频…
Hazelcast系列(九)：Map（一）加载和存储
系列文章
Hazelcast系列(一)：初识hazelcast
Hazelcast系列(二)：hazelcast集成（嵌入式）
Hazelcast系列(三)：hazelcast集成（服务器/客户端）
Hazelcast系列(四)：hazelcast管理中心 …
Leetcode刷题详解——岛屿数量
1. 题目链接：200. 岛屿数量
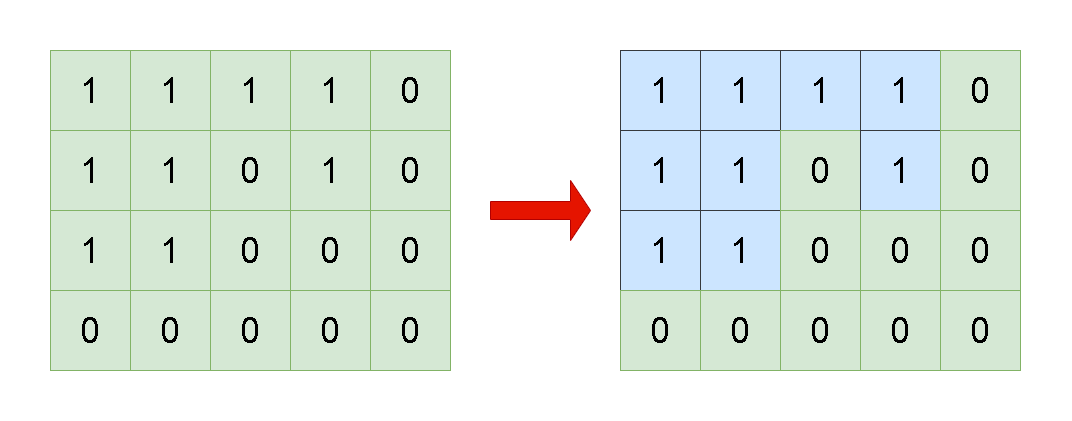
2. 题目描述： 给你一个由 1（陆地）和 0（水）组成的的二维网格，请你计算网格中岛屿的数量。 岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上…
JavaScript的函数的形参与实参是怎么回事
0 写在前面
此文给小白看的，如果不是可以直接关闭
1 讲解
例如JavaScript中定义函数
//定义函数
function 方法名(形参){方法体-->使用形参}//使用函数
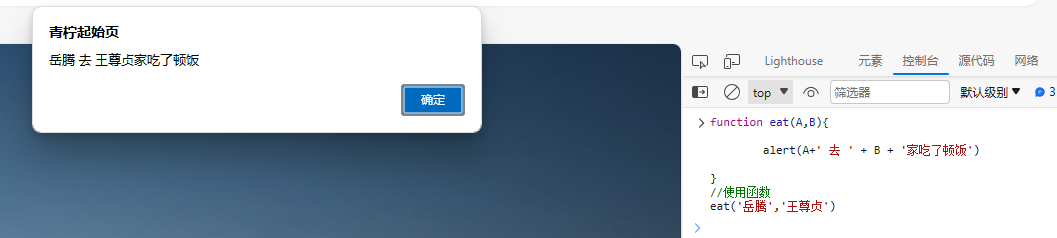
方法名字(实参)具体干了什么呢？此处以伪代码举例
//定义函数
function eat(A,B){A 去 B 家吃…
Unity中Shader的矩阵加减法
文章目录 前言一、什么是矩阵矩阵就是一组数的阵列 二、矩阵的加法三、矩阵的负值四、矩阵的减法五、矩阵的表示 前言
Unity中Shader用到的矩阵加减法，以及矩阵的一些基础常识 一、什么是矩阵
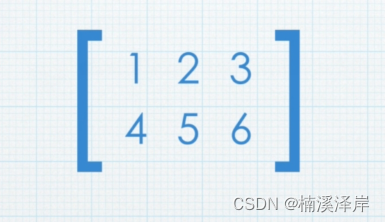
矩阵就是一组数的阵列
1 2 3 4 5 6 二、矩阵的加法
两个矩阵相加就是…
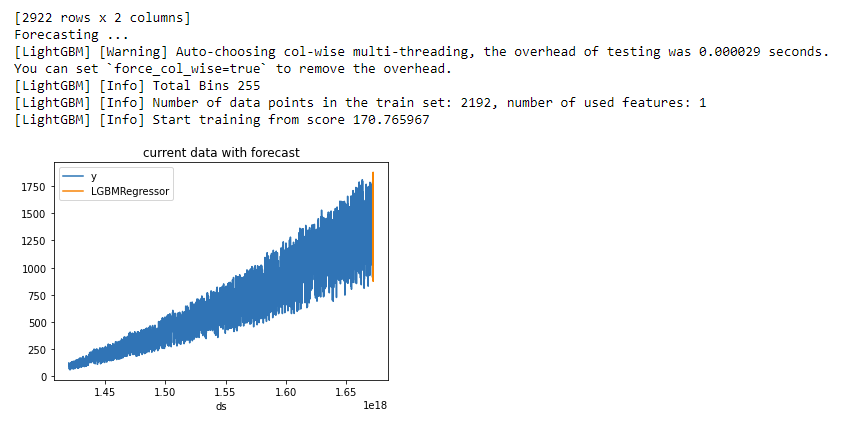
时序数据库 TDengine + 高级分析软件 Seeq，助力企业挖掘时序数据潜力
作为一款制造业和工业互联网（IIOT）高级分析软件，Seeq 支持在工艺制造组织中使用机器学习创新的新功能。这些功能使组织能够将自己或第三方机器学习算法部署到前线流程工程师和主题专家使用的高级分析应用程序，从而使单个数据科学家…
JavaScript学习_01——JavaScript简介
JavaScript简介 JavaScript介绍
JavaScript是一种轻量级的脚本语言。所谓“脚本语言”，指的是它不具备开发操作系统的能力，而是只用来编写控制其他大型应用程序的“脚本”。
JavaScript 是一种嵌入式（embedded）语言。它本身提供…
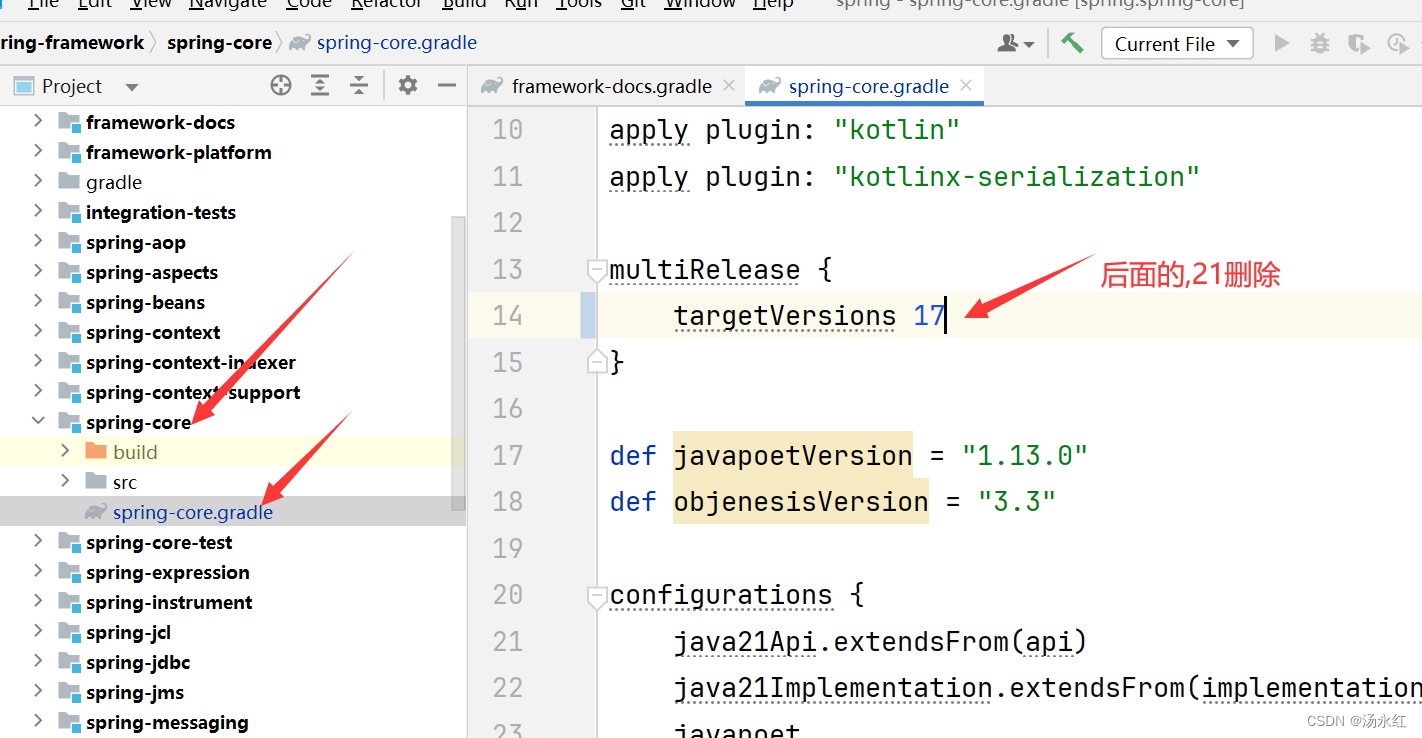
SpringBoot和Spring源码下载
1.下载：在一个空的干净地创建一个文件夹叫springsourcecode，其实叫什么都行的。
git clone https://github.com/spring-projects/spring-framework.git 2.JDK要和gradle匹配
我们要21的，今天为止2023年11月13日，idea是2023.2。 …
![[文件读取]Grafana未授权任意文件读取](https://img-blog.csdnimg.cn/dd6f4db1c1f5468195dbe3711c487d25.png)
[文件读取]Grafana未授权任意文件读取
1.1漏洞描述
漏洞编号Grafana未授权任意文件读取漏洞类型文件读取漏洞等级⭐⭐⭐漏洞环境VULFOCUS攻击方式 描述: Grafana是一个跨平台、开源的数据可视化网络应用程序平台。用户配置连接的数据源之后，Grafana可以在网络浏览器里显示数据图表和警告。 Grafana 存在…
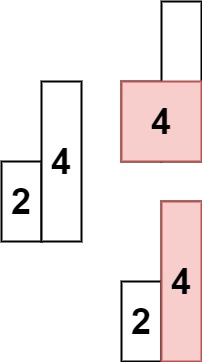
力扣第84 题柱状图中最大的矩形 C++ 单调栈 Java
题目
84. 柱状图中最大的矩形
困难
相关标签
栈 数组 单调栈
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。 示例 1: 输入：heigh…
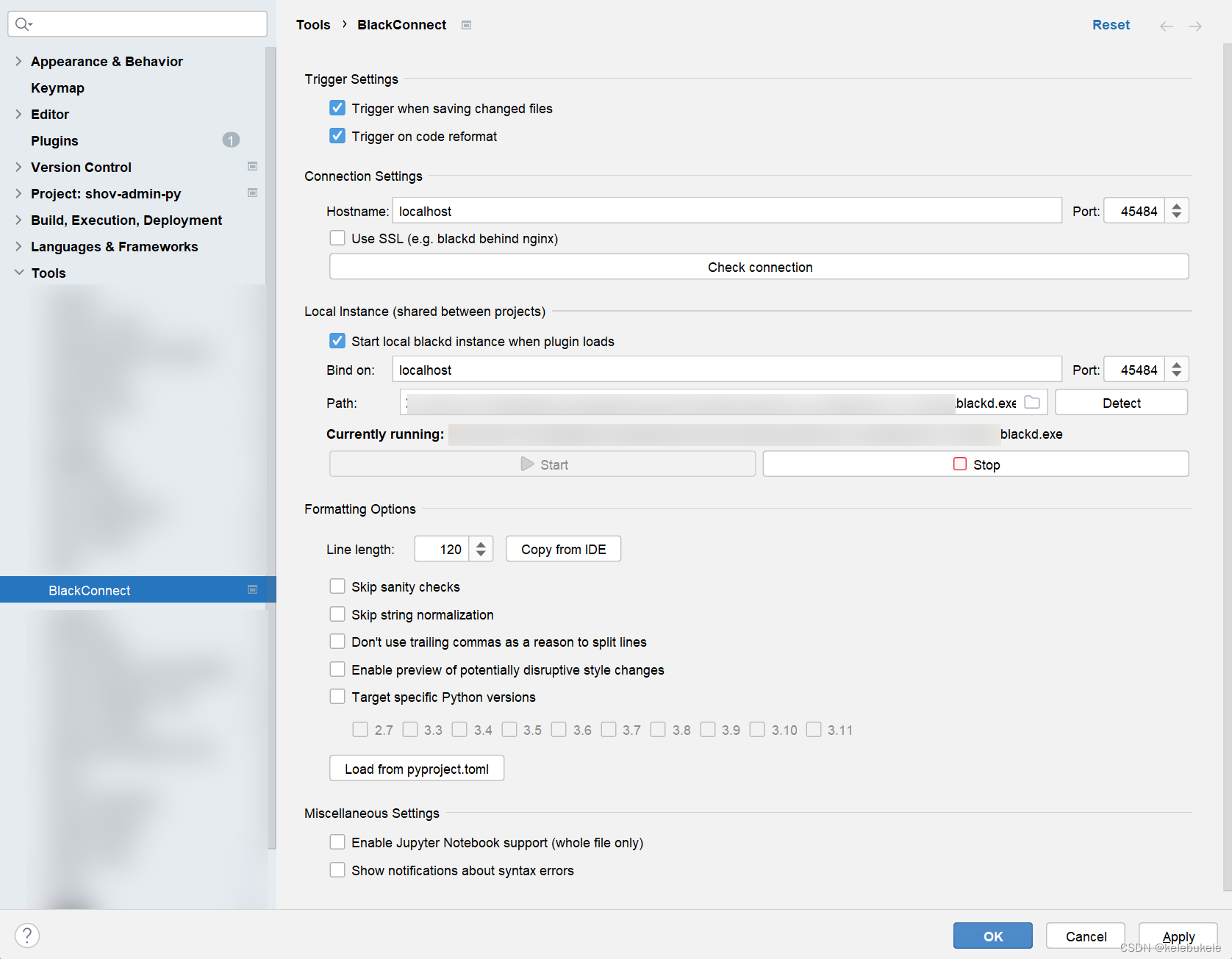
pycharm/vscode 配置black和isort
Pycharm blackd
Pycharm中有插件可以实现后台服务运行black：BlackConnect 安装 配置
Pycharm isort
pycharm中，isort没有插件，暂使用外部工具实现，外部工具也可添加快捷键实现快捷对文件、文件夹进行format import࿱…
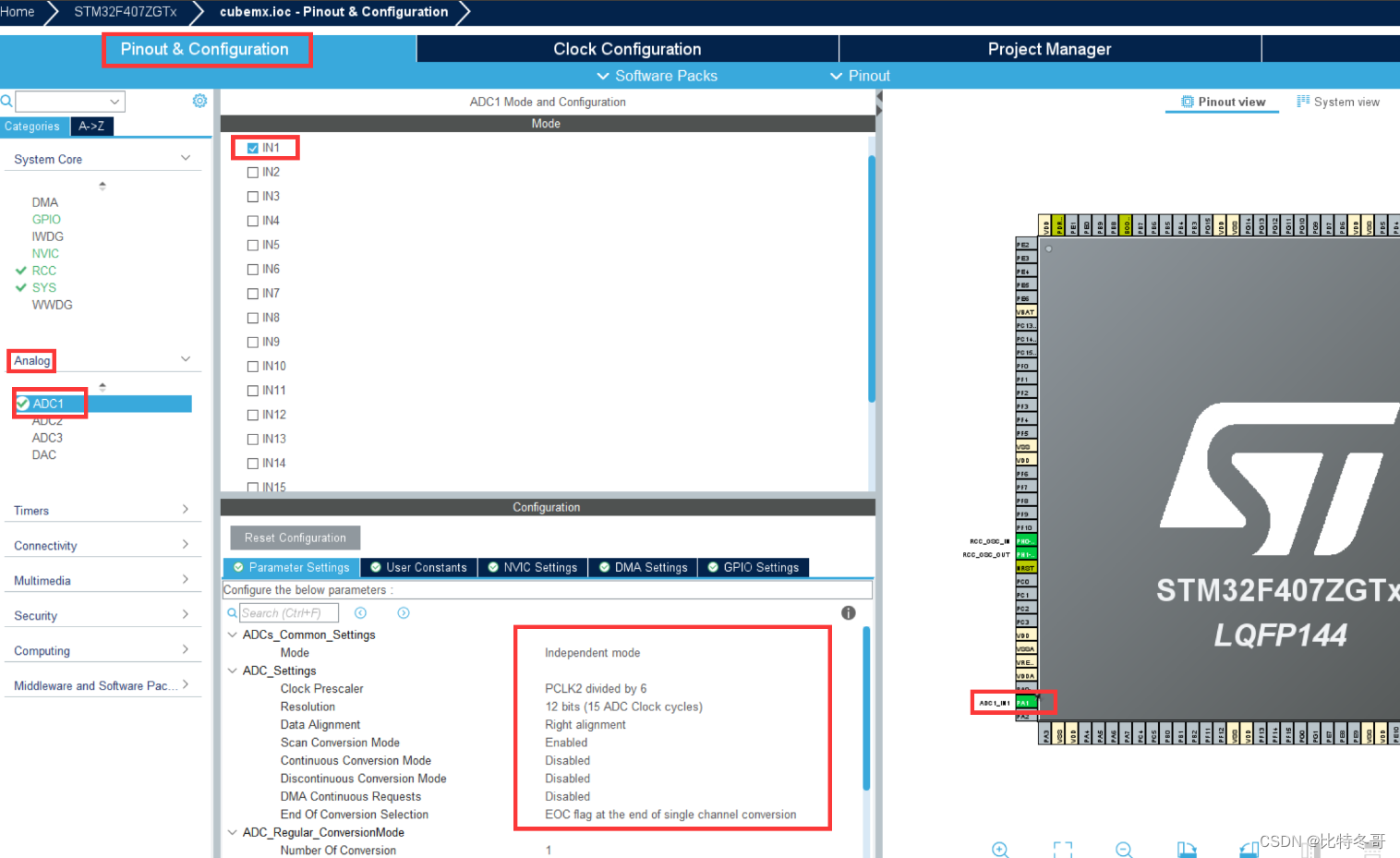
RT-Thread STM32F407 ADC
ADC(Analog-to-Digital Converter) 指模数转换器。是指将连续变化的模拟信号转换为离散的数字信号的器件。真实世界的模拟信号，例如温度、压力、声音或者图像等，需要转换成更容易储存、处理和发射的数字形式。模数转换器可以实现这个功能，在各…
什么是Vue.js中的单向数据流（one-way data flow）？为什么它重要？
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅：探索Web开发的奇妙世界 欢迎来到前端入门之旅！感兴趣的可以订阅本专栏哦！这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…
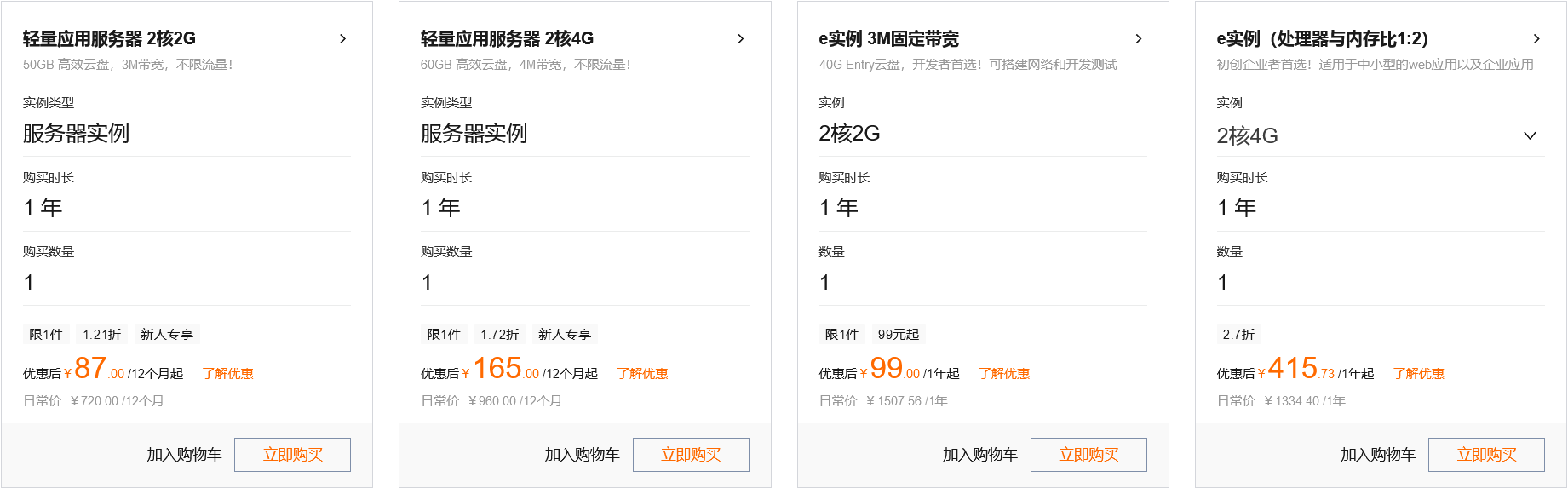
2核2G3M带宽云服务器99元（续费同价），阿里云老用户可买！
在阿里云的双11云服务器活动中，用户对轻量服务器2核2G3M带宽和经济型e实例2核2G配置3M带宽特别关注。除了这两款产品，阿里云还提供了其他性价比很高的云服务器配置，让用户有更多的选择。
经济型e实例2核2G3M配置99元一年是适用于个人和普通企…
C++11『右值引用 ‖ 完美转发 ‖ 新增类功能 ‖ 可变参数模板』
✨个人主页： 北 海 🎉所属专栏： C修行之路 🎃操作环境： Visual Studio 2022 版本 17.6.5 文章目录 🌇前言🏙️正文1.右值引用1.1.什么是右值引用？1.2.move 转移资源1.3.左值引用 vs …
鸿蒙：从0到“Hello Harmony”
效果展示 一.概述
明年华为鸿蒙就不再兼容Android生态了，作为拥有7亿终端用户的华为，建立自己的生态也是理所当然。
所以对HarmonyOS的研究也是众多开发者绕不开的坎了。
今天这篇博文主要实现一个“Hello Harmony！”的Demo。
二.官方链接…
从零搭建微服务架构：Spring Boot与Nacos完美整合
🎏：你只管努力，剩下的交给时间 🏠 ：小破站 从零搭建微服务架构：Spring Boot与Nacos完美整合 前言第一：服务注册与发现第二：配置中心第三：报错问题解决第四：什…