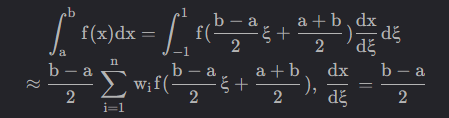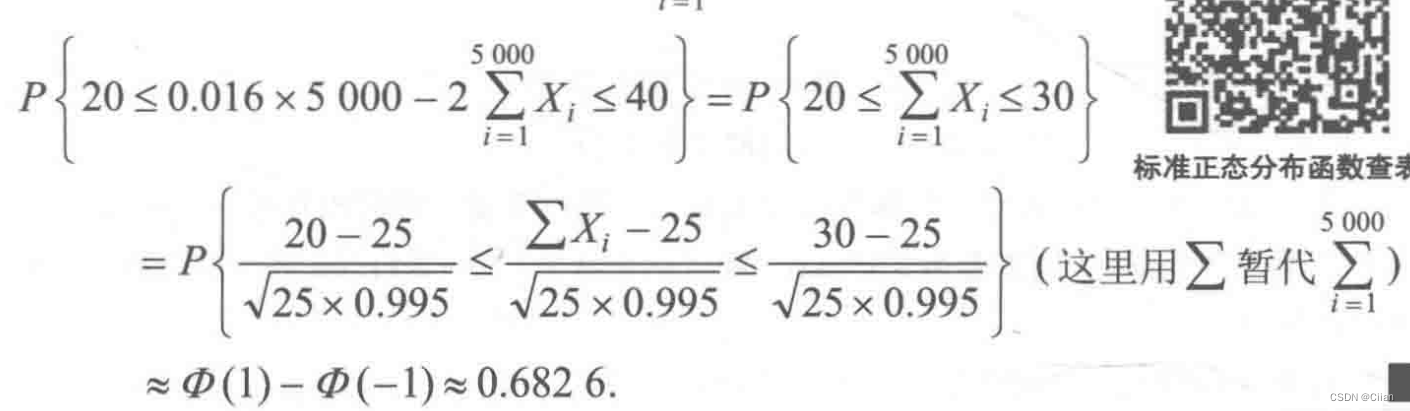本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/253656.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
css Vue尺子样式
原生css生成尺子样式
<template><div class"page"><div class"Light"></div><div class"rile"><ul id"list"><!--尺子需要几个单位就加几个--><li></li><li></li&…
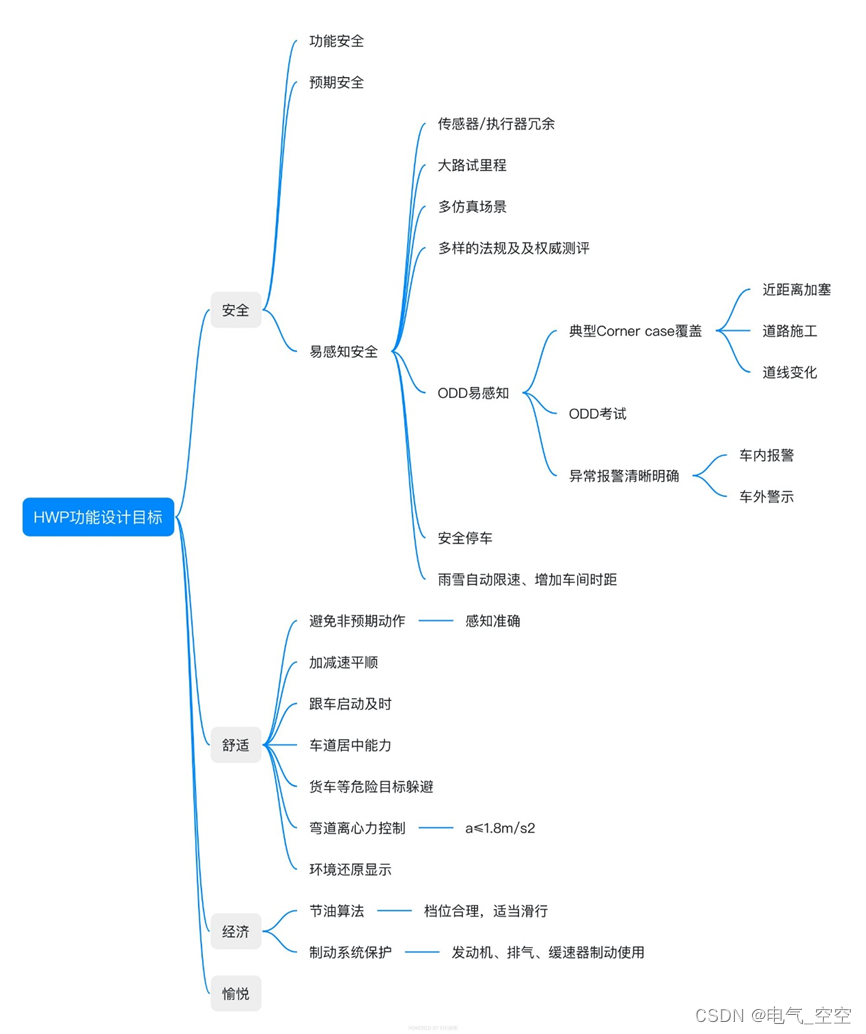
自动驾驶HWP功能规范
HWP功能规范
Highway Pilot Functional Specification 文件状态: 【√】草稿 【】正式发布 【】正在修改 文件起草分工 撰写: 审核: 编制: 签名: 日期: 审核: 签名: 日期&am…
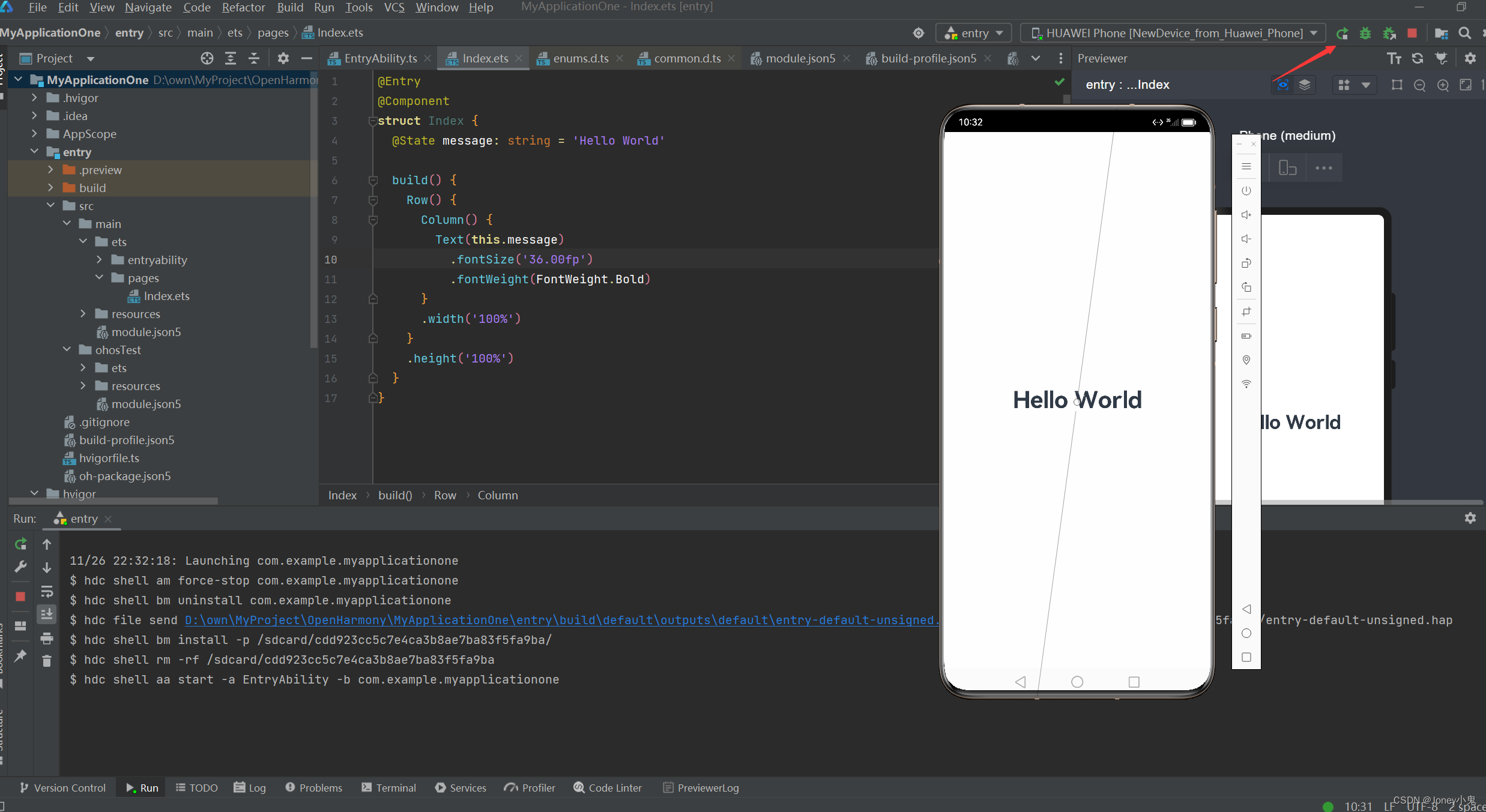
Harmony入门-HelloWorld
HarmonyOS 已经出来一些时间了。也有了OpenHarmony,作为HarmonyOS抽离的基础架构OpenHarmony,贡献给开源了,后续独立出来,那可真是就要独立生态啦,咱们顺水行舟,学习学习。
1.IDE 安装 https://hmxt.org/d…
用python实现kindle文件转换pdf
上一篇文章讲了下用工具转换相关的格式:https://blog.csdn.net/weixin_42019349/article/details/134654695
今天来分享一个python库实现上述功能,实现文件转换自由 ^_^ 主角就是pypandoc库
# 安装方式
pip install pypandoc# pypandoc主要有三个函数…
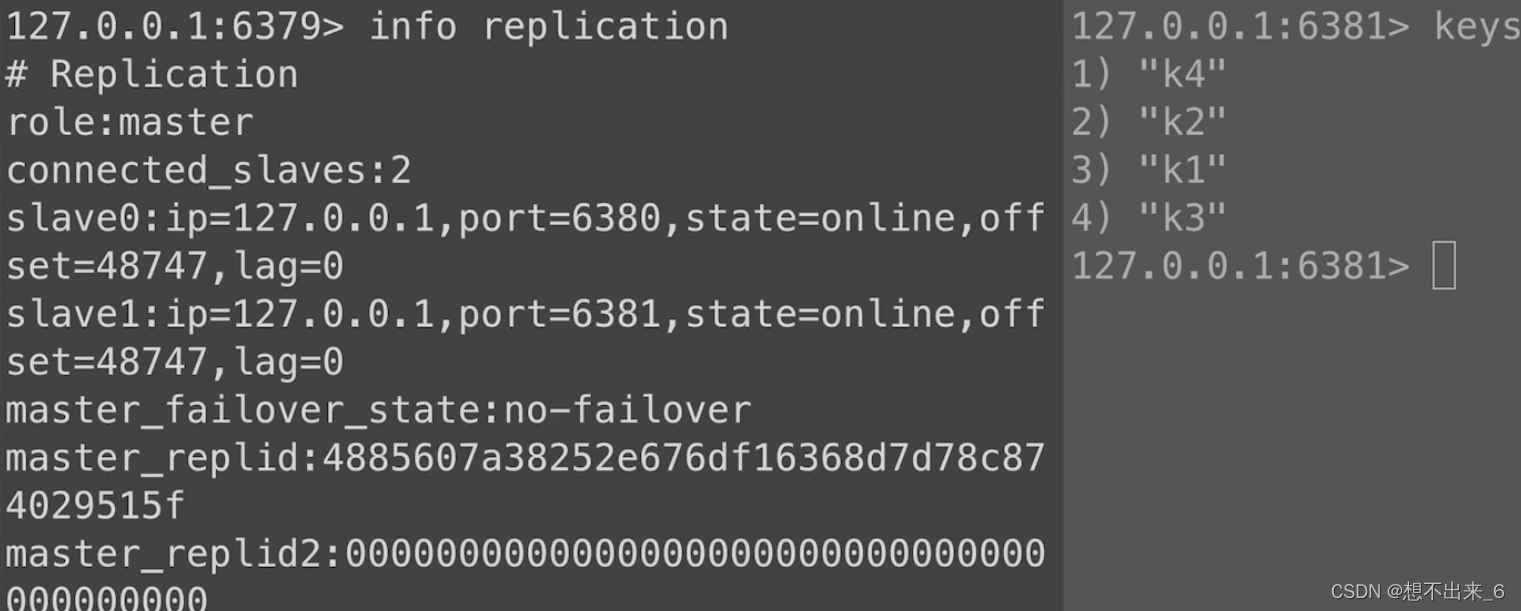
Redis(主从复制)
主从复制:
主从复制是指在Redis中,一个主节点可以将自己的数据复制到多个从节点上,从节点会定期从主节点同步数据,从而保持数据的一致性。主从复制可以实现数据的备份和容灾,提高系统的可用性和性能。在主从复制中&am…
【Dockerfile】将自己的项目构建成镜像部署运行
目录
1.Dockerfile
2.镜像结构
3.Dockerfile语法
4.构建Java项目
5.基于Java8构建项目
1.Dockerfile
常见的镜像在DockerHub就能找到,但是我们自己写的项目就必须自己构建镜像了。
而要自定义镜像,就必须先了解镜像的结构才行。
2.镜像结构
镜…
【MyBatisPlus】通俗易懂 快速入门 详细教程
目录
学习目标
一、MyBatisPlus简介
1. 入门案例
问题导入
1.1 SpringBoot整合MyBatisPlus入门程序
①:创建新模块,选择Spring初始化,并配置模块相关基础信息
②:选择当前模块需要使用的技术集(仅保留JDBC&…
每日一题:LeetCode-202.快乐数(一点都不快乐)
每日一题系列(day 06)
前言:
🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🔎…
python实现数值积分
目录 1、求解问题
2、求解原理
3、python实现 1、求解问题 2、求解原理
高斯-勒让德数值积分是一种有效的数值积分方法,它结合了高斯点和勒让德函数来计算一维函数的积分。
高斯-勒让德求积公式在给定的积分区间[a, b]上,通过选择一些特定的点&#…
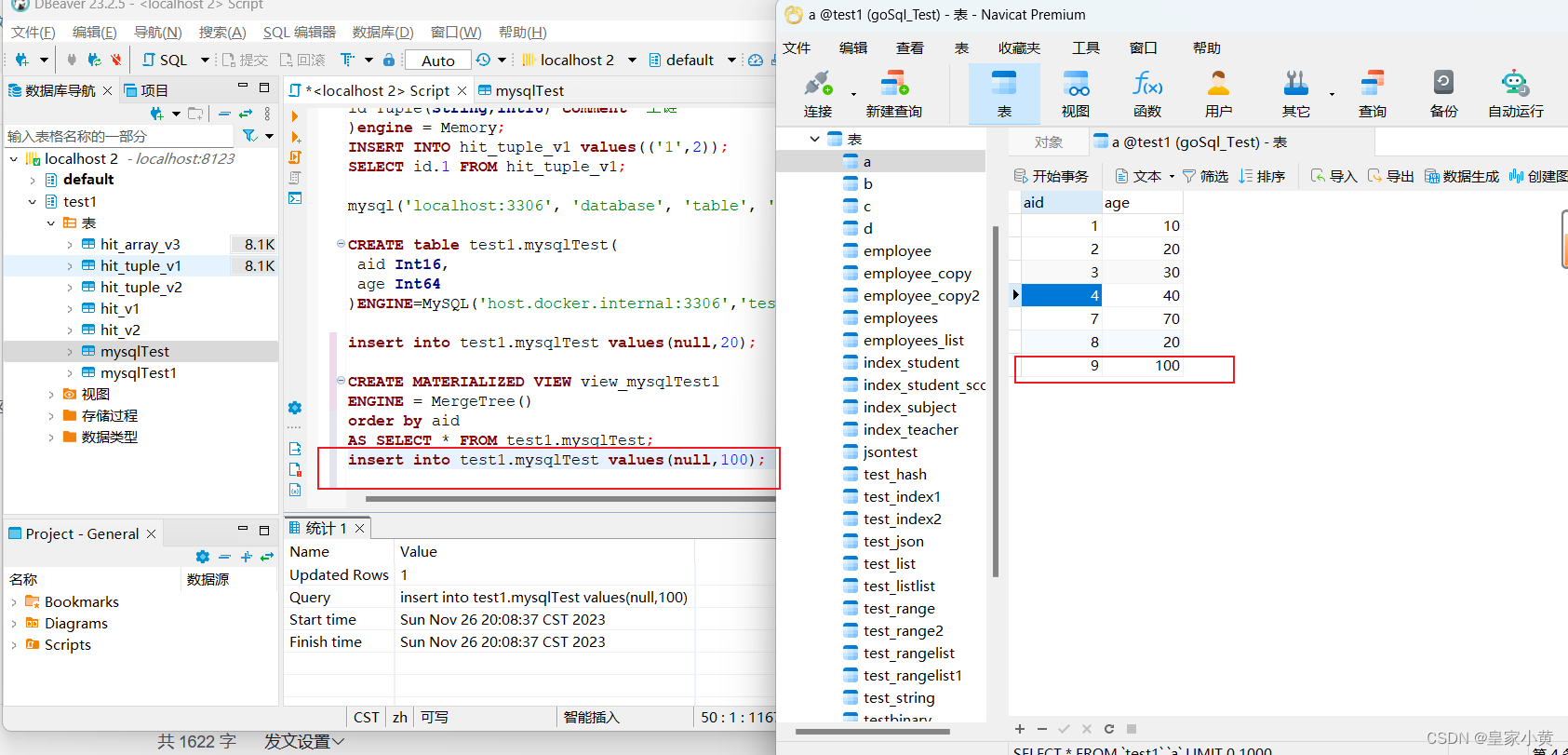
windows本地dockr的clickhouse链接本地mysql服务,连接不上
不想看过成的,解决办法在最后面
报错信息:
SQL 错误 [1000] [08000]: Poco::Exception. Code: 1000, e.code() 0, Exception: Connections to all replicas failed: test1localhost:3306 as user root (version 21.12.3.32 (official build)) , serve…
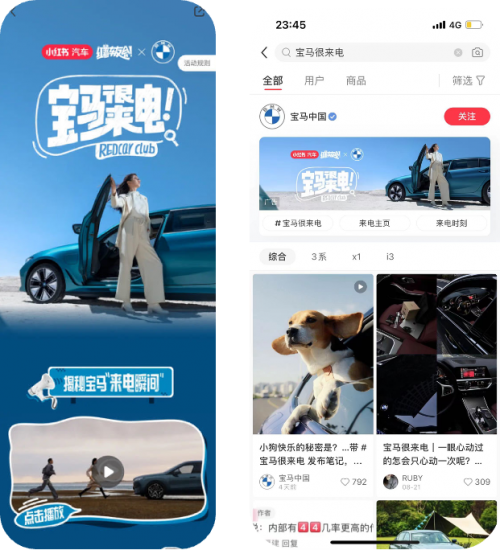
形象建设、生意经营、用户运营,汽车品牌如何在小红书一举多得?
随着小红书在多领域的持续成长,现在来小红书看汽车的用户,需求逐渐多元化与专业化。近1年的时间,有超过1亿人在小红书「主动搜索」过汽车内容,大家已经不仅限于玩车、用车,更是扩展到了百科全书式的看、选、买、学各个…
概率论与数理统计-第4章 随机变量的数字特征
第4章 随机变量的数字特征
4.1数学期望
一、离散型随机变量的数学期望
定义1设离散型随机变量X的概率分布为 P{Xxi}pi,i1,2,…,如果级数绝对收敛,则定义X的数学期望(又称均值)为
二、连续型随机变量的数学期望
定义2设X是连续型随机变量…
YOLOv8优化策略:自适应改变核大小卷积AKConv,效果优于标准卷积核和DSConv |2023.11月最新成果
🚀🚀🚀本文改进: AKConv 中,通过新的坐标生成算法定义任意大小的卷积核的初始位置。 为了适应目标的变化,引入了偏移量来调整每个位置的样本形状。 此外,我们通过使用具有相同大小和不同初始采样形状的 AKConv 来探索神经网络的效果。 AKConv 通过不规则卷积运算完成…
01-鸿蒙4.0学习之开发环境搭建 HelloWorld
HarmonyOS开发学习
1.环境配置
1.下载地址
开发工具:DevEco Studio 3.1.1 Release
下载地址
安装选择快捷方式 安装nodejs和Ohpm 安装SDK 选择同意Accept 检测8项目是否安装成功 2.创建项目 —— hello word
PT里如何针对某个模块设置false path
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧?
拾陆楼知识星球入口 如题,这个问题实际上讲的是get_cells的用法,我们要抓取某个模块内的全部cell,在ICC2里可以get_flat_cells xx/xx/module_name*,但…
第二节HarmonyOS DevEco Studio创建项目以及界面认识
一、创建项目
如果你是首次打开DevEco Studio,那么首先会进入欢迎页。 在欢迎页中单击Create Project,进入项目创建页面。 选择‘Application’,然后选择‘Empty Ability’,单击‘Next’进入工程配置页。 配置页中,详…
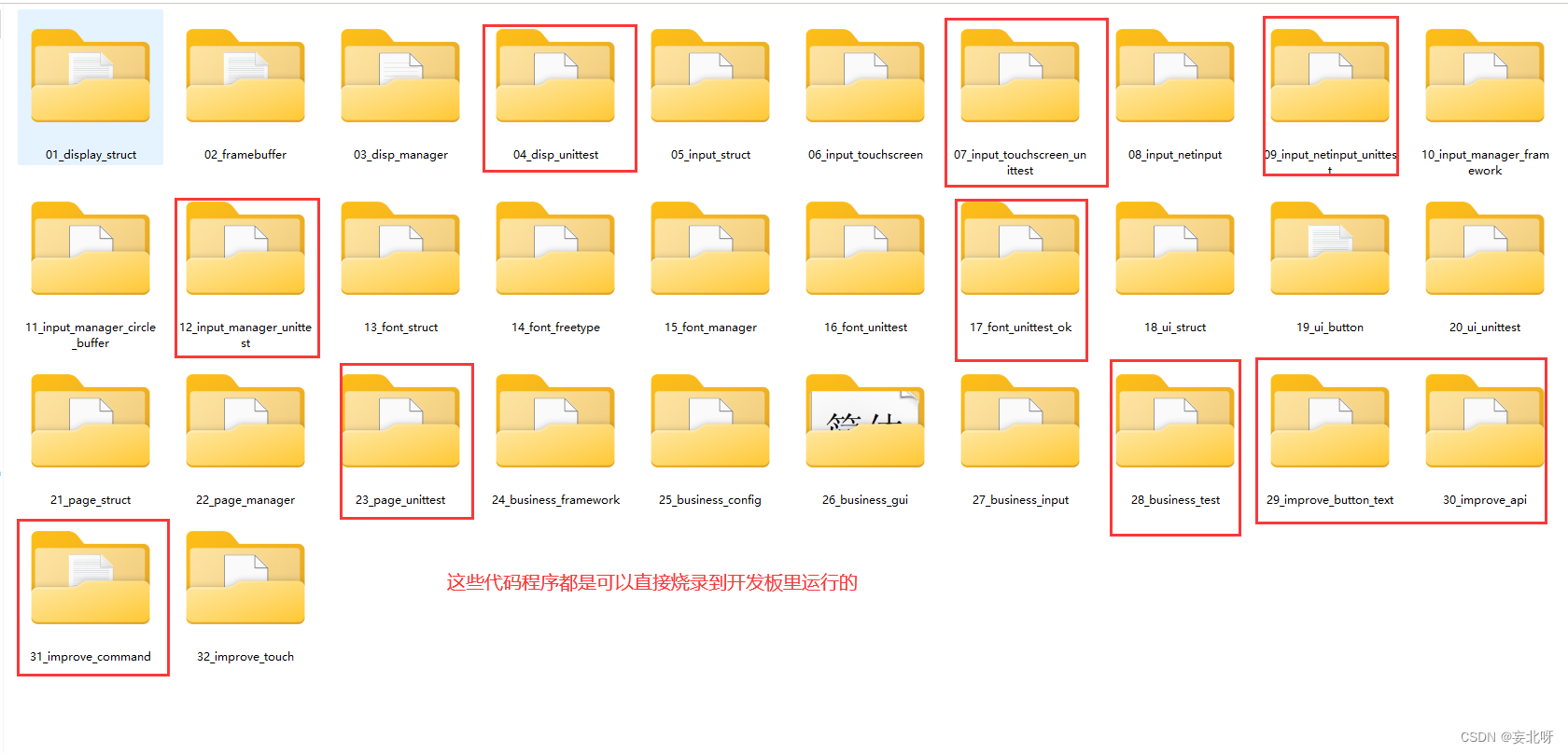
Linux基础项目开发1:量产工具——程序框架(一)
前言: 前面已经将Linux应用开发基础知识学习完了,现在让我们来做个小项目练练手,对之前的一些知识点进行一个更加具体详细的认识与了解,我们要进行的项目名称为:电子产品量产测试与烧写工具,这是一套软件&a…