本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.ldbm.cn/p/320843.html
如若内容造成侵权/违法违规/事实不符，请联系编程新知网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
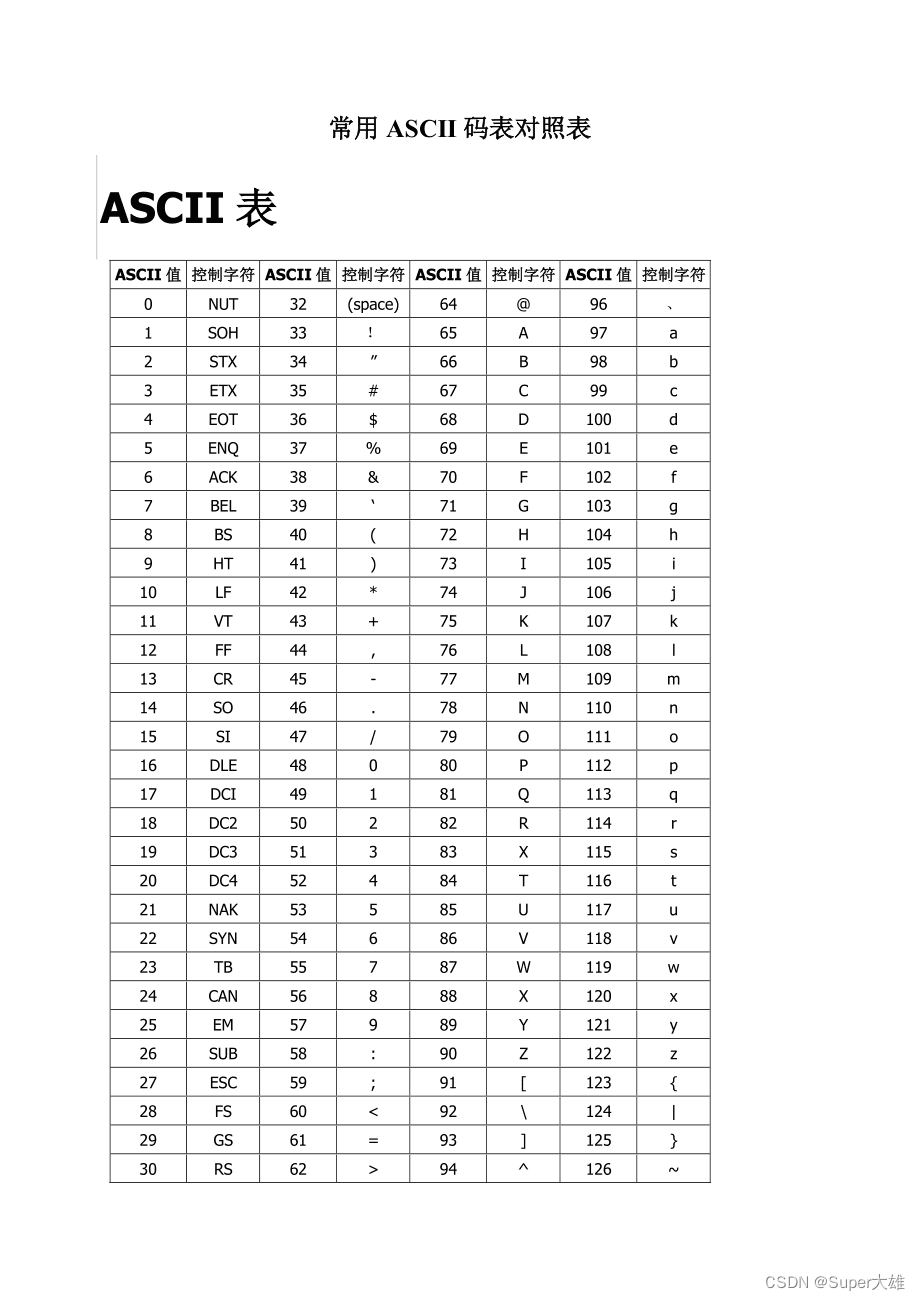
C++入门学习（九）浮点数
浮点型主要有两种：
floatdouble
占用空间有效数字范围float4字节7位有有效数字double8字节15~16位有效数字 为什么float 有效数位 7 or 8 位，double 15 or 16 位？ https://zhidao.baidu.com/question/1182732476020869219.htmlhttps://zhid…
a-table 边框颜色修改
案例：
<template><div class"mod_table"><a-table :columns"columns":data-source"data" bordered:pagination"false"></a-table></div>
</template>
<script>
export default…
PICO Developer Center 创建和调试 ADB 命令
PICO 开发者中心概览
ADB 是一个轻量级的 Android 调试桥(Android Debug Bridge，简称 ADB)，用于与 Android 设备进行通信和调试。ADB提供了许多有用的功能，使开发人员能够轻松地管理和调试设备上的应用程序。
你可以使用 PDC 工具来调试系统…
一个非常流行的R语言调色板：RColorBrewer
R 语言有许多非常优秀的调色板，本文就介绍一个非常流行的，我也经常在用的调色板 R 包：RColorBrewer。 安装 install.packages("RColorBrewer") 加载 library(RColorBrewer)
library(knitr) 初探 ?RColorBrewer 在帮助页面可以看到…
【算法练习Day50】下一个更大元素II接雨水
📝个人主页：Sherry的成长之路 🏠学习社区：Sherry的成长之路（个人社区） 📖专栏链接：练题 🎯长路漫漫浩浩，万事皆有期待 文章目录 下一个更大元素II接雨水单调…
uni-app中代理的两种配置方式
方式一:
在项目的 manifest.json 文件中点击 源码视图 在最底部的vue版本下编写代理代码 方式二:
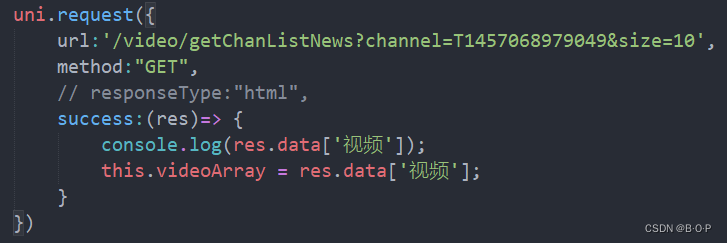
在项目中创建 vue.config.js 文件然后进行配置 在页面中发起请求
完整的url：http://c.m.163.com/recommend/getChanListNews?channelT1457068979049&size10 …
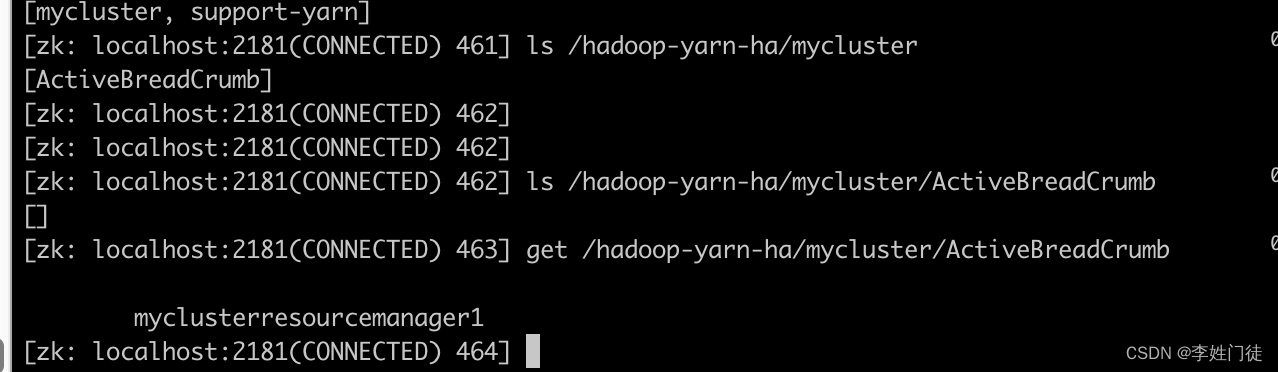
YARN节点故障的容错方案
YARN节点故障的容错方案 1. RM高可用1.1 选主和HA切换逻辑 2. NM高可用2.1 感知NM节点异常2.2 异常NM上的任务处理 4. 疑问和思考4,1 RM感知NM异常需要10min，对于app来说是否太长了？ 5. 参考文档 本文主要探讨yarn集群的高可用容错方案和容错能力的探讨。…
【备战蓝桥杯】探索Python内置标准库collections的使用
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-q0zvWxZtAIdSGZ8R {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…
77. 组合 - 力扣（LeetCode）
题目描述 给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
输入示例
n 4, k 2输出示例
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]解题思路 我们使用回溯、深度优先遍历的思想，我们使用一个栈 path…
Git学习笔记（第2章）：Git安装
官网地址：Githttps://git-scm.com/ Step1：查看Git的GNU协议 → 点击“Next” Step2：设置Git的安装位置(非中文、无空格的目录) → 点击“Next” Step3：选择Git的选项配置(推荐默认设置) → 点击“Next” Step4：设置Git…
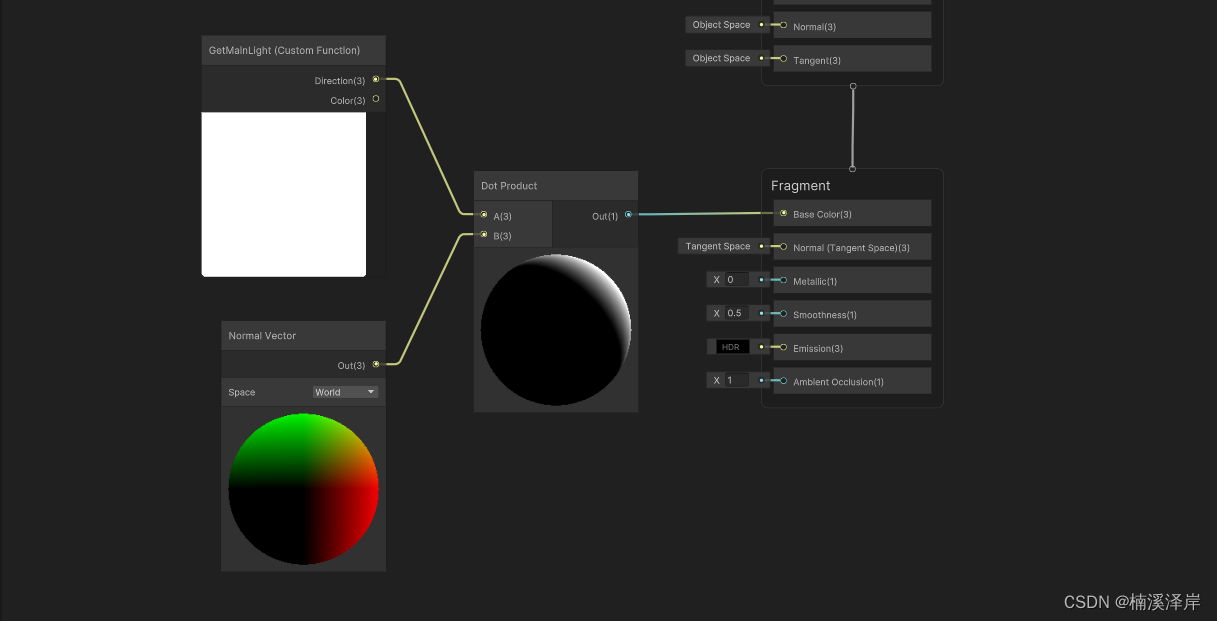
Unity中ShaderGraph下获取主灯
文章目录 前言一、ShaderGraph获取主灯1、创建ShaderGraph2、创建一个自定义方法（Custom Function）节点3、新建两个 Vector3 类型的输出变量4、选择自定义节点程序体为 string 类型5、编写程序体6、我们输出主光方向看看效果7、我们输出主光颜色看看效果…
基于python深度学习对起痘原因识别-含数据集和代码
数据集介绍，下载本资源后，界面如下： 有一个文件夹一个是存放数据集的文件。
数据集介绍：
一共含有:2个类别，包含:mosquito, tick等。 然后本地的train.txt和val.txt里面存放的是数据集的图片路径和对应的标签。 运行…
【迅搜19】扩展（二）TNTSearch和JiebaPHP方案
扩展（二）TNTSearch和JiebaPHP方案 搜索引擎系列的最后一篇了。既然是最后一篇，那么我们也轻松一点，直接来看一套非常有意思的纯 PHP 实现的搜索引擎及分词方案吧。这一套方案由两个组件组成，一个叫 TNTSearch …
Redis: Redis介绍
文章目录 一、redis介绍二、通用的命令三、数据结构1、字符串类型（String）（1）介绍（2）常用命令（3）数据结构 2、列表（List）（1）介绍&…
![[小程序]基于token的权鉴测试](https://img-blog.csdnimg.cn/direct/40acf7c0bfaa4c6790d340be0ac3bcf4.png)
[小程序]基于token的权鉴测试
一、服务器配置 服务器基于flask，需要额外安装flask_jwt_extended包
from flask import Flask #导入Flask包
from flask import request
from flask import jsonify #用来返回json消息
from flask_jwt_extended import create_access_token, jwt_requi…
Linux指令补充和权限简单介绍
一.tar指令
形式：tar [-cxtzjvf] 文件与目录 ....
参数：
-c ：建立一个压缩文件的参数指令(create 的意思)； -x ：解开一个压缩文件的参数指令！ -t ：查看 tarfile 里面的文件！ -…
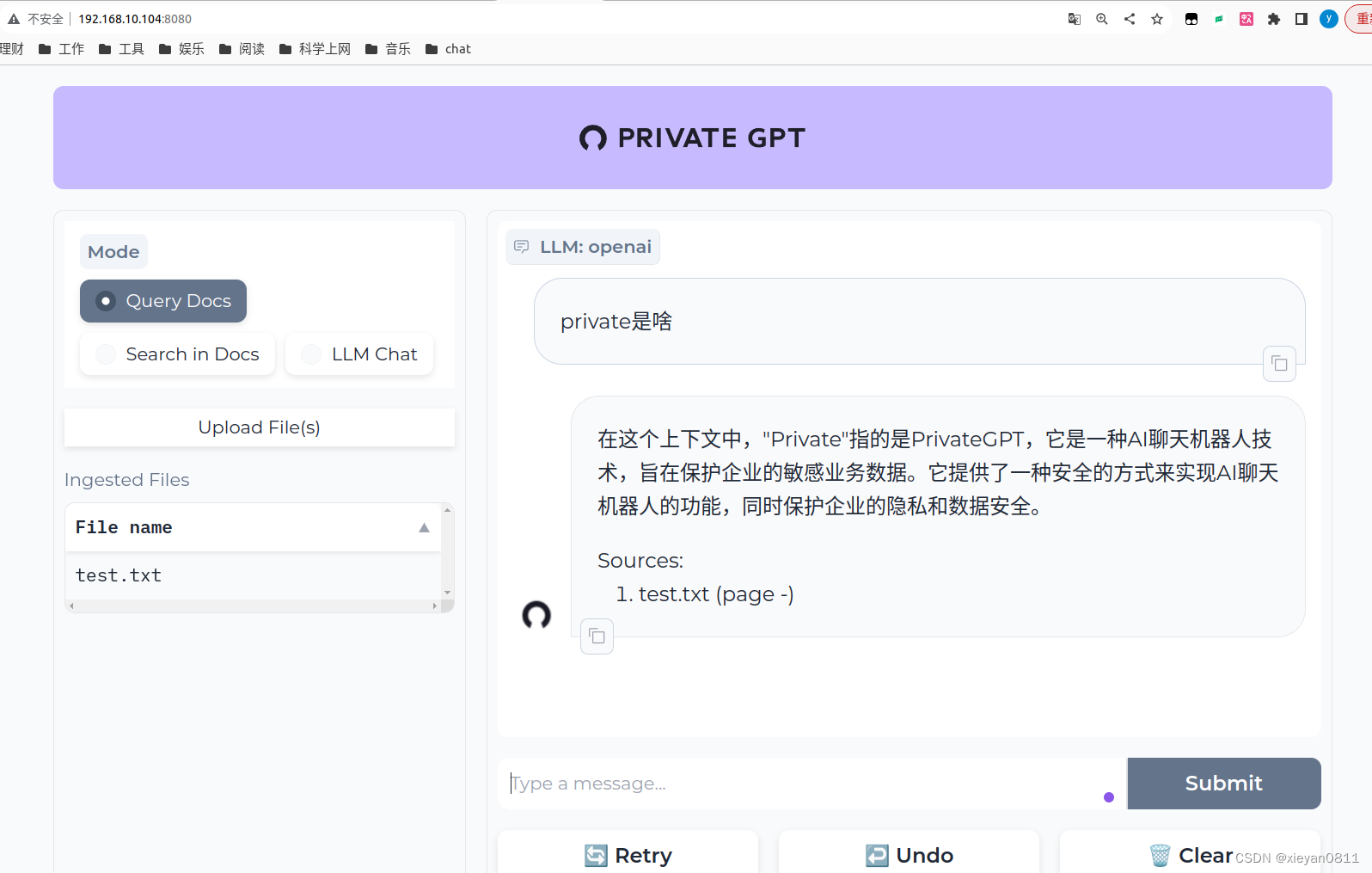
GPT应用_PrivateGPT
项目地址：https://github.com/imartinez/privateGPT 1 功能
1.1 整体功能，想解决什么问题
搭建完整的 RAG 系统，与 FastGPT 相比，界面比较简单。但是底层支持比较丰富，可用于知识库的完全本地部署，包含大…
vcsVerdi常见操作技巧一
1. Verdi 如何将已经设置好的nSchematic view 保存下来，方便下次的使用
Step1：点击file的save_session，进去后直接保存文件； Step2：下一次进入后打开nSchem后在此打开file点击restore session（save sessio…
【蓝桥杯日记】复盘篇一：深入浅出顺序结构
🚀前言 本期是一篇关于顺序结构的题目的复盘,通过复盘基础知识，进而把基础知识学习牢固！通过例题而进行复习基础知识。 🚩目录
前言
1.字符三角形 分析：
知识点：
代码如下
2. 字母转换
题目分析:
知…
Kotlin 尾递归函数
函数式编程中，重要的概念 尾递归。 当一个函数，在函数最后调用 自身，称为 尾递归，是一种特殊的递归函数。 在JVM中，每次方法调用时，都会产生新的栈帧（stack frame），消耗栈…