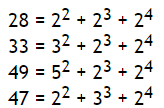本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/322370.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Oracle篇—分区表和分区索引的介绍和分类(第一篇,总共五篇)
☘️博主介绍☘️: ✨又是一天没白过,我是奈斯,DBA一名✨ ✌✌️擅长Oracle、MySQL、SQLserver、Linux,也在积极的扩展IT方向的其他知识面✌✌️ ❣️❣️❣️大佬们都喜欢静静的看文章,并且也会默默的点赞收藏加关注❣…
【MySQL】最左匹配原则
最左匹配原则
0x1 简单说下什么是最左匹配原则
顾名思义:最左优先,以最左边的为起点任何连续的索引都能匹配上。同时遇到范围查询(>、<、between、like)就会停止匹配。 例如:b 2 如果建立(a,b)顺序…
【江科大】STM32:(超级详细)定时器输出比较
文章目录 输出比较单元特点 高级定时器:均有4个通道 PWM简介PWM(Pulse Width Modulation)脉冲宽度调制输出比较通道PWM基本结构基本定时器 参数计算捕获/比较通道的输出部分详细介绍如下: 舵机介绍硬件电路 直流电机介绍ÿ…
随机森林中每个树模型分裂时的特征选取方式
随机森林中每个树模型分裂时的特征选取方式
随机森林中每个树模型的每次分裂都是基于随机选取的特征子集进行分裂的。
具体来说,对于每个决策树,在每个节点的分裂过程中,随机森林算法会从原始特征集合中随机选择一个特征子集,然…
Docker基础语法
目录
一.docker安装
二.docker基础名词
三.docker基础命令
四.命令别名
五.数据卷
六.挂载本地目录或文件
七.Docker镜像
八.网络 一.docker安装
1.安装yum工具 yum install -y yum-utils device-mapper-persistent-data lvm2
2.安装 docker yum源 yum-config-manag…
Mapbox加载浙江省天地图服务和数据处理
1. 加载影像服务
通过浙江省天地图官网申请所需服务,使用token获取服务数据
由于浙江省天地图使用的坐标系是 cgcs2000,需要使用 的框架对应为 cgcs2000/mapbox-gl,通过cdn引入或npm下载
影像服务地址为: ‘https://ditu.zjzw…
【RT-DETR有效改进】 主干篇 | SwinTransformer替换Backbone(附代码 + 详细修改步骤 +原理介绍)
前言
大家好,这里是RT-DETR有效涨点专栏。
本专栏的内容为根据ultralytics版本的RT-DETR进行改进,内容持续更新,每周更新文章数量3-10篇。
专栏以ResNet18、ResNet50为基础修改版本,同时修改内容也支持ResNet32、ResNet101和PP…
回溯算法篇-01:全排列
力扣46:全排列 题目分析
这道题属于上一篇——“回溯算法解题框架与思路”中的 “元素不重复不可复用” 那一类中的 排列类问题。
我们来回顾一下当时是怎么说的: 排列和组合的区别在于,排列对“顺序”有要求。比如 [1,2] 和 [2,1] 是两个不…
牛客竞赛算法入门题单打卡 K Number
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网
题目描述
We define Shuaishuai-Number as a number which is the sum of a prime square(平方), prime cube(立方), and prime fourth power(四次方).
The first four Shuaishuai numbers a…
如何才能拥有比特币 - 01 ?
如何才能拥有BTC
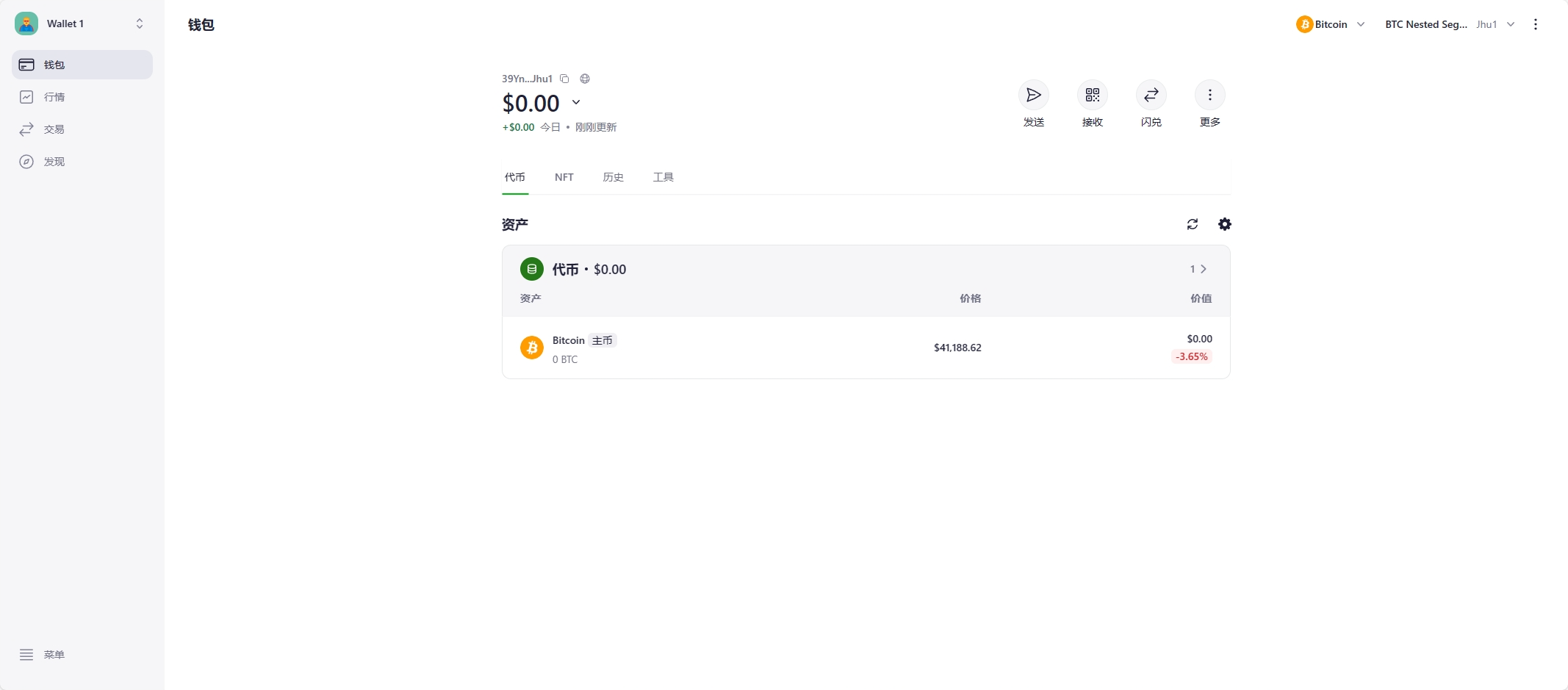
在拥有 BTC 之前我们要先搞明白 BTC到底保存在哪里?我的钱是存在银行卡里的,那我的BTC是存在哪里的呢?
BTC到底在哪里?
一句话概括,BTC是存储在BTC地址中,而且地址是公开的,…
苹果笔记本MacBook电脑怎么卸载软件?三种方法快速卸载软件
苹果笔记本MacBook电脑是一款非常流行的电脑,但是有时候我们可能需要卸载一些不需要的软件。下面是一些简单的步骤,可以帮助您在MacBook电脑上卸载软件。
苹果笔记本MacBook电脑怎么卸载软件?三种实用方法快速卸载软件! 方法一&a…
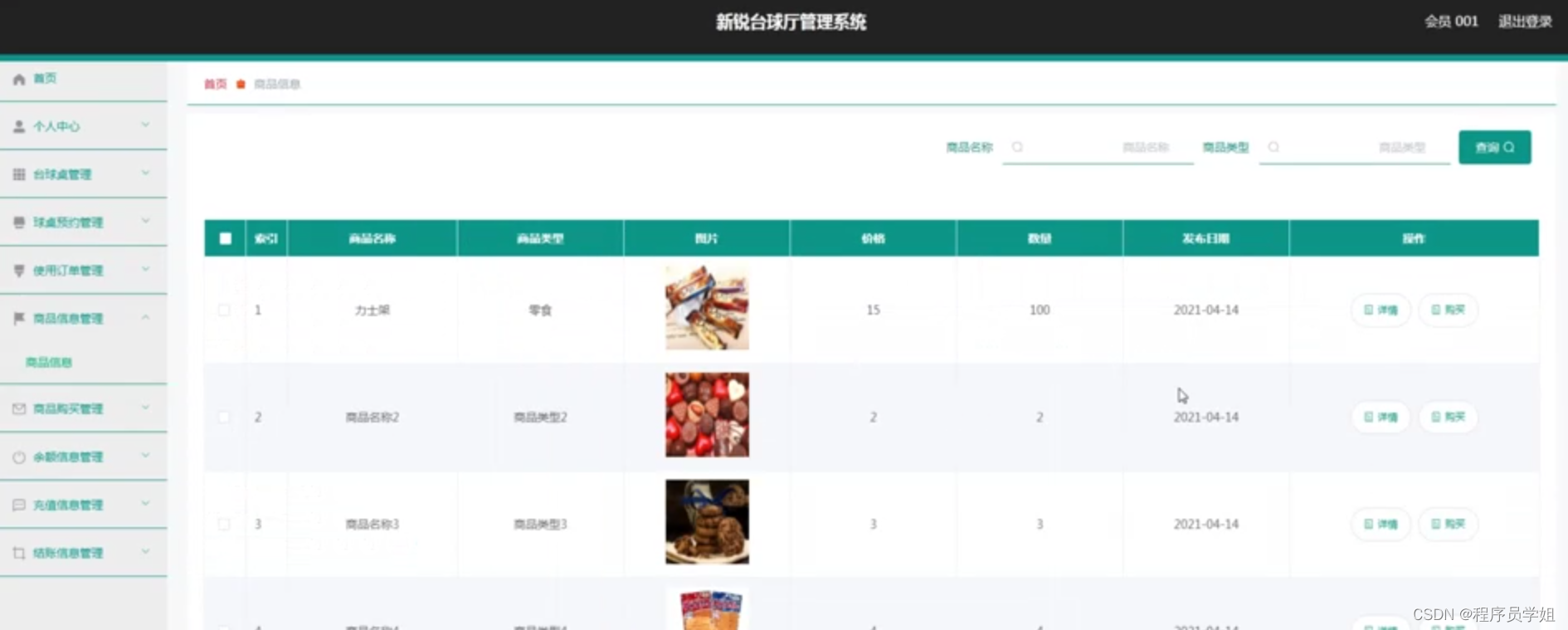
基于springboot+vue的台球管理系统
摘要 台球管理系统是一款基于Spring Boot和Vue.js技术栈构建的现代化系统,旨在提供全面而高效的台球场馆管理服务。该系统通过整合前后端技术,实现了场馆预约、会员管理、比赛统计等核心功能,为台球场馆管理员和玩家提供了便捷、智能的管理和…
力扣hot100 环形链表 快慢指针 哈希 数学公式
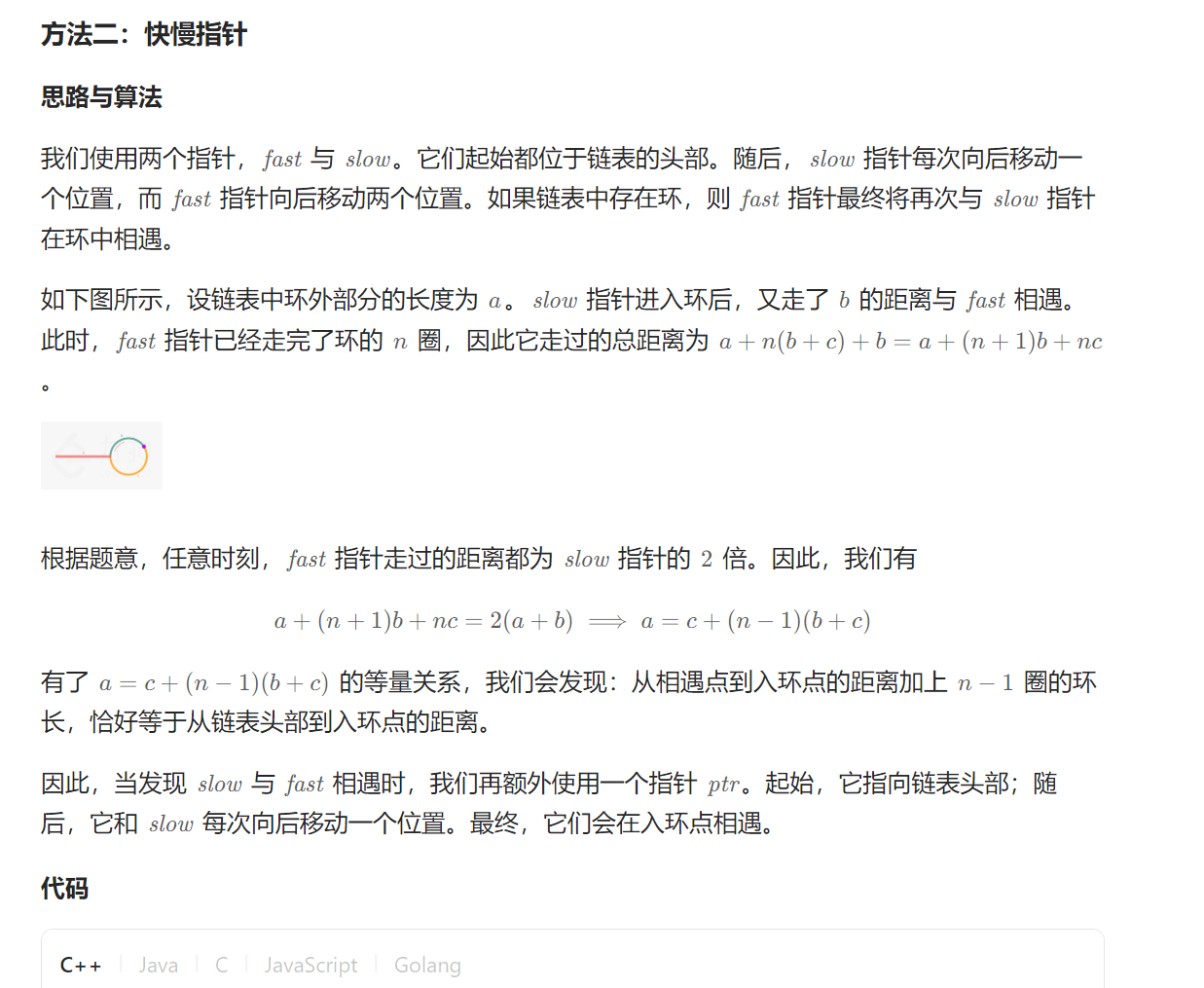
Problem: 142. 环形链表 II 文章目录 思路Code 思路
👨🏫 参考题解
Code
⏰ 时间复杂度: O ( n ) O(n) O(n) 🌎 空间复杂度: O ( 1 ) O(1) O(1)
/**
/*** Definition for singly-linked list.* class ListNode {* int val;* …
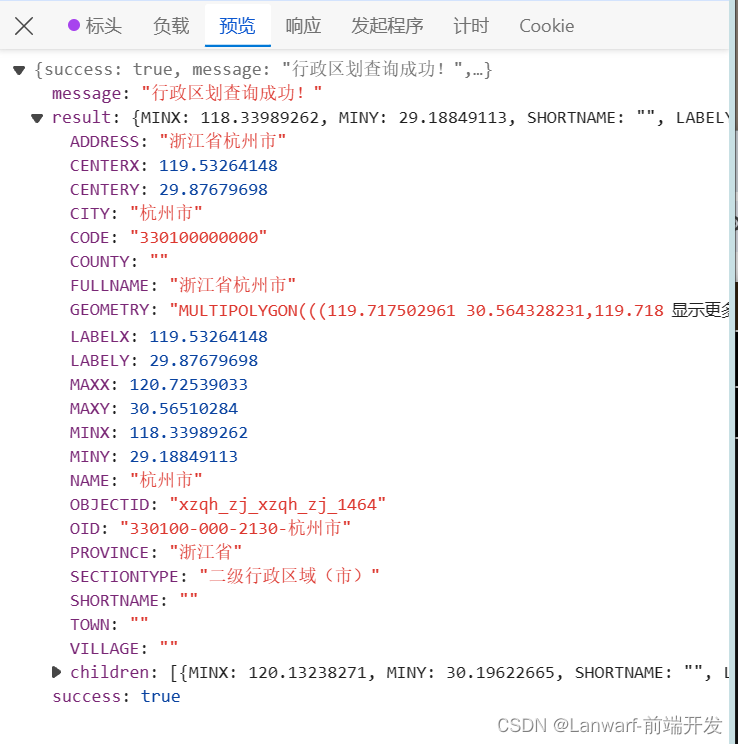
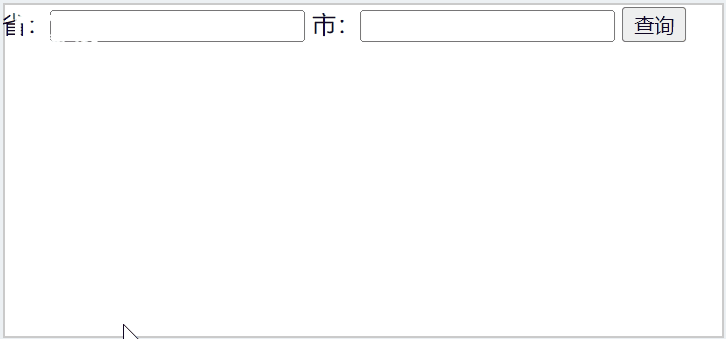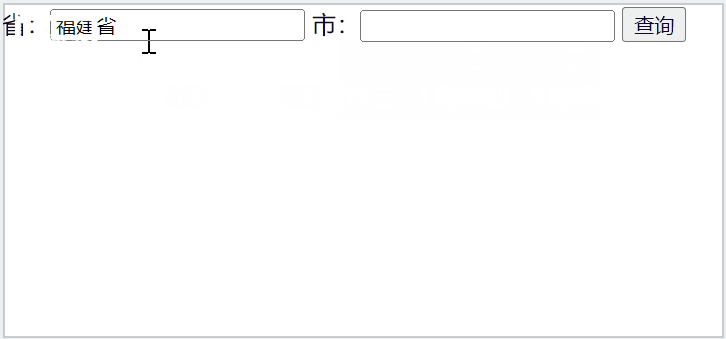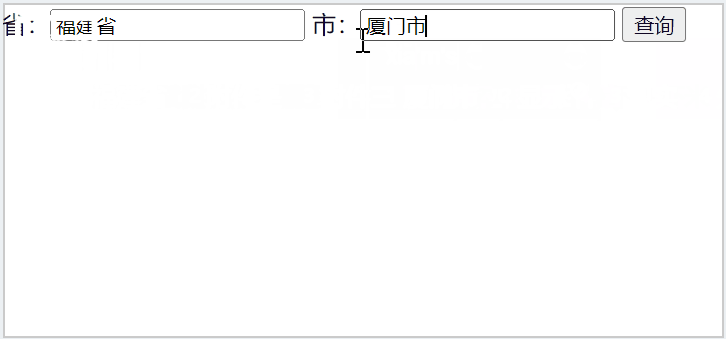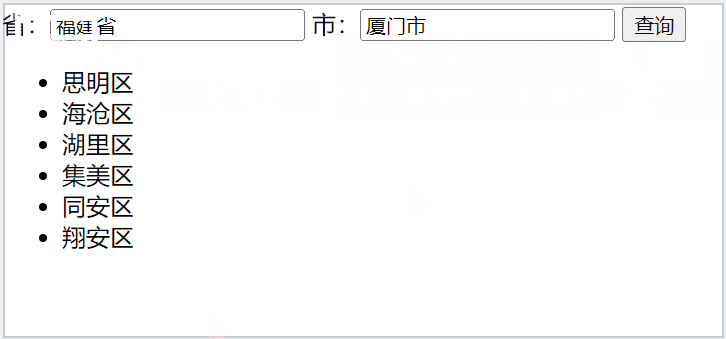
黑马axios案例之地区查询
查询某个省内某个城市的所有地区 接口:http://hmajax.itheima.net/api/area 参数名: pname:省份名字或直辖市名字,比如北京、福建省、辽宁省… cname:城市名字,比如北京市、厦门市、大连市…
<!DOCTYPE html>
<html lang"en&q…
深度学习(5)---自注意力机制
文章目录 1. 输入与输出2. Self-attention2.1 介绍2.2 运作过程2.3 矩阵相乘理解运作过程 3. 位置编码4. Truncated Self-attention4.1 概述4.2 和CNN对比4.3 和RNN对比 1. 输入与输出 1. 一般情况下在简单模型中我们输入一个向量,输出结果可能是一个数值或者一个类…
SpringBoot+Email发送邮件
引言
邮件通知是现代应用中常见的一种通信方式,特别是在需要及时反馈、告警或重要事件通知的场景下。Spring Boot提供了简单而强大的邮件发送功能,使得实现邮件通知变得轻而易举。本文将研究如何在Spring Boot中使用JavaMailSender实现邮件发送…
ChatGPT与生成式AI在教育领域的应用前景光明,但也伴随着挑战
随着ChatGPT和其他生成式AI技术,如GPT-3.5、GPT-4的出现,我们正见证教育领域一场前所未有的变革浪潮。这些技术不仅推动了教育方式的进步,也为学习者带来了全新的机遇和挑战。 NO.1 教育变革的新浪潮
生成式AI技术,特别是ChatGPT…
springboot 项目,返回的实体类里面字段是null ,现在想要为空应该是““,空字符串,而不是null
目录 1 问题2 实现 1 问题
返回给前端的数据,如果数据库的字段没有数据,给返回的是null 要变成这个,全局都变成这样 2 实现
springboot返回给页面的json数据中,如果有数据为null,则返回空字符串。
springboot默认使…
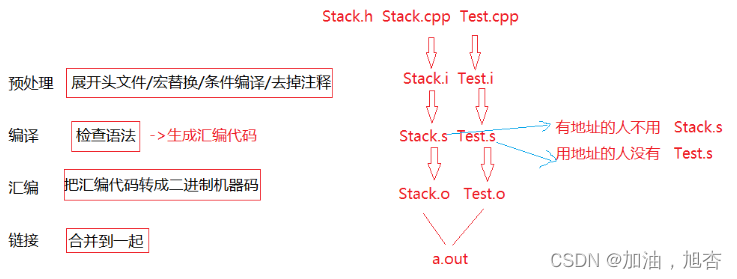
【C++语言1】基本语法
前言 💓作者简介: 加油,旭杏,目前大二,正在学习C,数据结构等👀 💓作者主页:加油,旭杏的主页👀 ⏩本文收录在:再识C进阶的专栏…
算法通关村番外篇-面试150题一
大家好我是苏麟 , 今天开始LeetCode面试经典150题 . 大纲 26. 删除有序数组中的重复项80. 删除有序数组中的重复项 II 26. 删除有序数组中的重复项
描述 :
给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 …