本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/349621.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
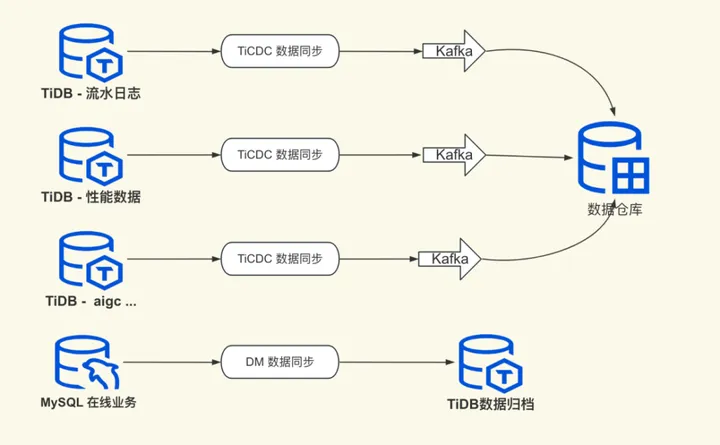
作业帮 x TiDB丨多元化海量数据业务的支撑
导读
作业帮是一家成立于 2015 年的在线教育品牌,致力于用科技手段助力教育普惠。经过近十年的积累,作业帮运用人工智能、大数据等技术,为学生、老师、家长提供学习、教育解决方案,智能硬件产品等。随着公司产品和业务场景越来越…
Django实战:部署项目 【资产管理系统】,Django完整项目学习研究(项目全解析,部署教程,非常详细)
导言
关于Django,我已经和大家分享了一些知识,考虑到一些伙伴需要在实际的项目中去理解。所以我上传了一套Django的项目学习源码,已经和本文章进行了绑定。大家可以自行下载学习,考虑到一些伙伴是初学者,几年前&#…
notepad++打开文本文件乱码的解决办法
目录
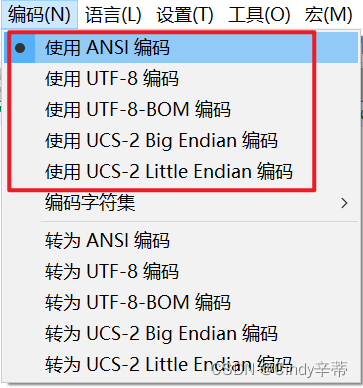
第一步 在编码菜单栏下选择GB2312中文。如果已经选了忽略这一步
第二步 点击编码,红框圈出来的一个个试。我切换到UTF-8编码就正常了。 乱码如图。下面分享我的解决办法 第一步 在编码菜单栏下选择GB2312中文。如果已经选了忽略这一步 第二步 点击编码&#…
Qt C++春晚刘谦魔术约瑟夫环问题的模拟程序
什么是约瑟夫环问题?
约瑟夫问题是个有名的问题:N个人围成一圈,从第一个开始报数,第M个将被杀掉,最后剩下一个,其余人都将被杀掉。例如N6,M5,被杀掉的顺序是:5ÿ…
OAuth2.0 最简向导
本文是一篇关于OAuth2.0的启蒙教程,图文并茂,通俗易懂,力求用最简洁明了的方式向初学者解释OAuth2.0是什么。本文并不是冗杂难懂的长篇大论,一图胜千言,深入浅出OAuth2.0,知其然知其所以然。
参考文献
首…
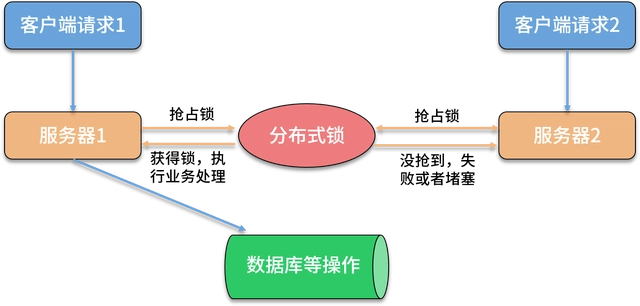
分布式锁的应用场景及实现
文章目录 分布式锁的应用场景及实现1. 应用场景2. 分布式锁原理3. 分布式锁的实现3.1 基于数据库 分布式锁的应用场景及实现
1. 应用场景
电商网站在进行秒杀、特价等大促活动时,面临访问量激增和高并发的挑战。由于活动商品通常是有限库存的,为了避免…
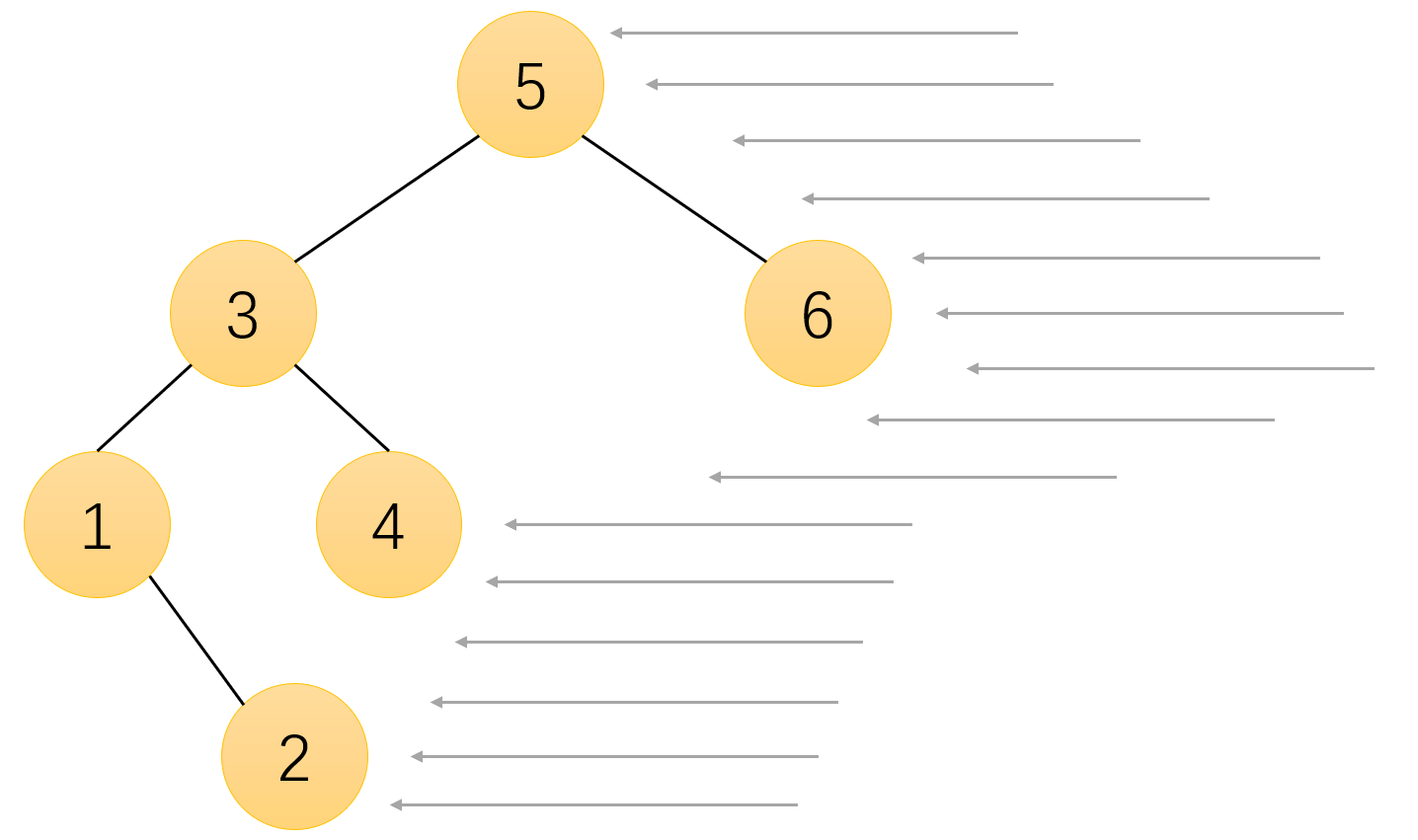
LeetCode 热题 100 | 二叉树(中下)
目录
1 基础知识
1.1 队列 queue
1.2 栈 stack
1.3 常用数据结构
1.4 排序
2 98. 验证二叉搜索树
3 230. 二叉搜索树中第 K 小的元素
4 199. 二叉树的右视图 菜鸟做题忘了第几周,躺平过了个年TT 1 基础知识
1.1 队列 queue
queue<type> q…
vue 使用Html2Canvas对元素截图 下载
介绍 官网:https://html2canvas.hertzen.com/ 一款轻量化的网页截图工具,可以对元素截图下载,只有几十KB,很强大,例如程序发送错误,就可以调用方法继续截图,或者用户在干什么都可以继续记录。
…
Linux 主机数据拷贝与 Linux 服务器之间拷贝文件的方法
Linux 主机数据拷贝与 Linux 服务器之间拷贝文件的方法 1. 使用 scp 命令2. 使用 rsync 命令3. 使用 scp 和 rsync 的图形界面工具4. 使用 FTP/SFTP 协议总结与比较 在 Linux 系统中,数据拷贝是日常操作中的常见需求,尤其是在不同主机或服务器之间进行文…
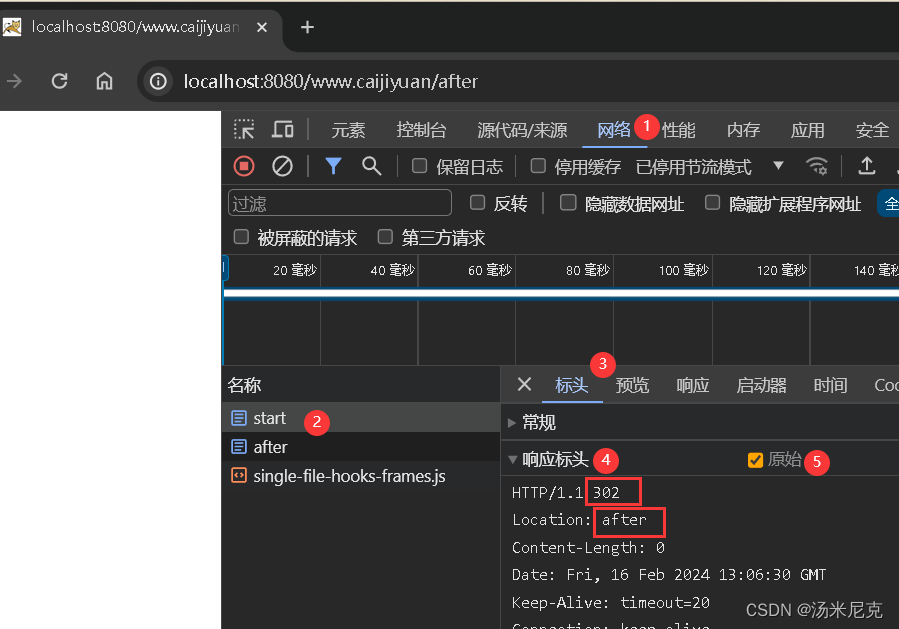
板块一 Servlet编程:第四节 HttpServletResponse对象全解与重定向 来自【汤米尼克的JAVAEE全套教程专栏】
板块一 Servlet编程:第四节 HttpServletResponse对象全解与重定向 一、什么是HttpServletResponse二、响应数据的常用方法三、响应乱码问题字符流乱码字节流乱码 四、重定向:sendRedirect请求转发和重定向的区别 在上一节中,我们系统的学习了…
python的安装,Django的安装,Pycharm新建Django项目
环境准备
python的安装
官网:https://www.python.org
官网–>downloads–>windows–>选择对应的版本下载.exe文件>>> 双击运行下载的安装包,按步骤进行安装
①选择安装方式
install now,会直接默认安装到C盘中&#x…
07-k8s中secret资源02-玩转secret
一、回顾secret资源的简单实用 第一步:将想要的数据信息【key:value】中的value值,使用base64编码后,写入secret资源清单中; 第二步:创建secret资源; 第三步:pod资源引用secret资源&…
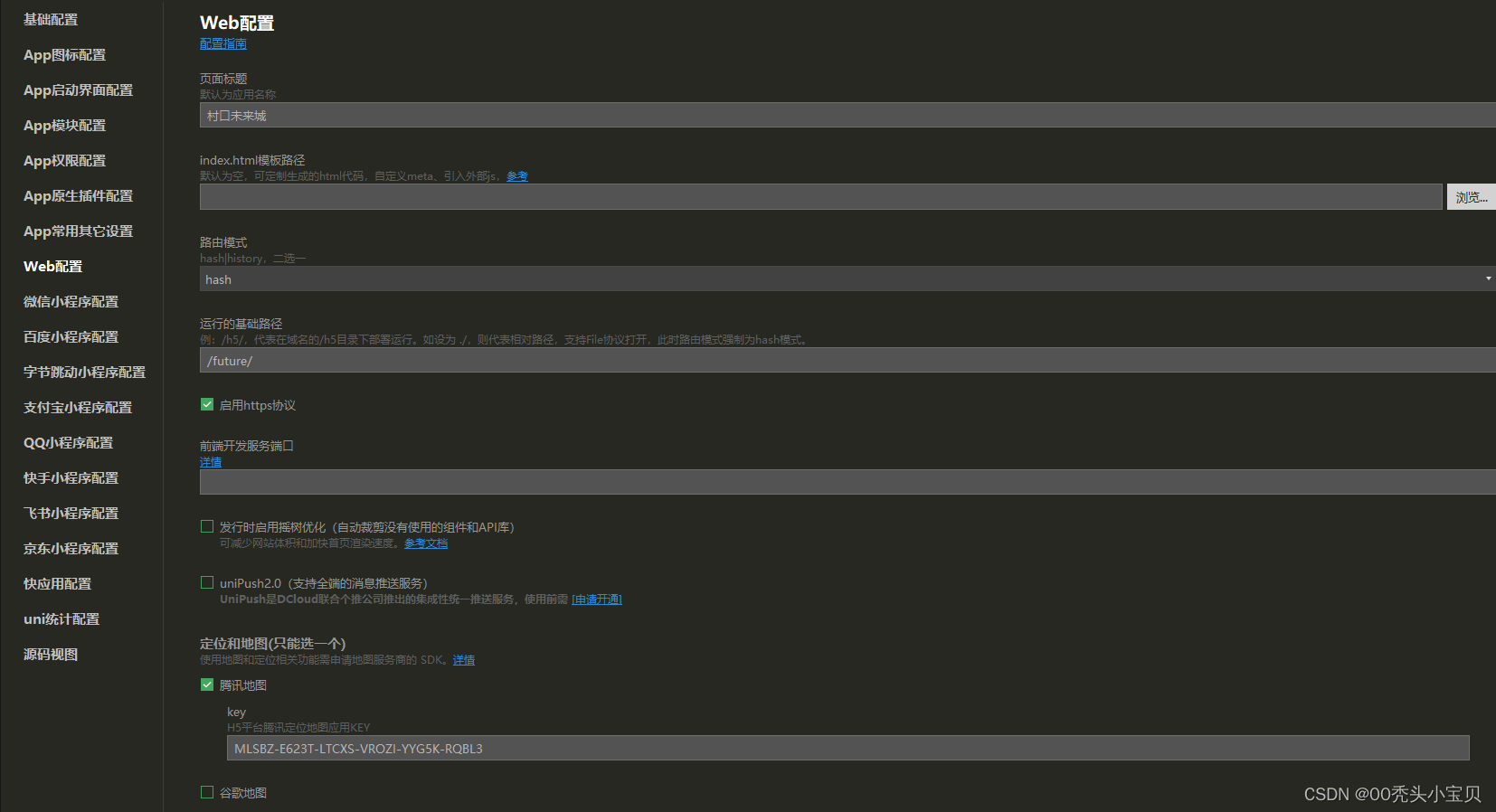
uniapp项目准备工作
1.封装请求
export const baseUrl
function getHeaders () {let token uni.getStorageSync(token)let header {"access-token":token,// X-Requested-With: XMLHttpRequest,Content-Type: application/json; charsetUTF-8}return header
}
function reLogin(){/…
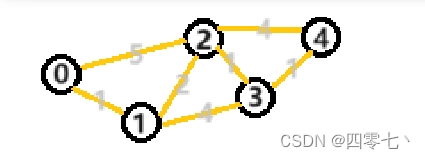
数据结构-最短路径(Dijkstra算法与Floyd算法)
介绍
对于网图来说,最短路径是指两顶点之间经过的边上权值之和最少的路径,其路径上第一个点记为源点,最后一个为终点。
计算最短路径有两个经典算法,即迪杰斯特拉(Dijkstra)算法与弗洛伊德(Fl…
手持三防平板丨国产化加固平板丨国产三防平板发展的意义是什么?
随着现代科技的快速发展,平板电脑在我们的生活中扮演着越来越重要的角色。然而,传统的平板电脑只能在普通的环境中使用,而无法在恶劣的环境中使用,例如在高海拔、高温、高湿度、沙漠等环境中,传统平板电脑往往会出现故…
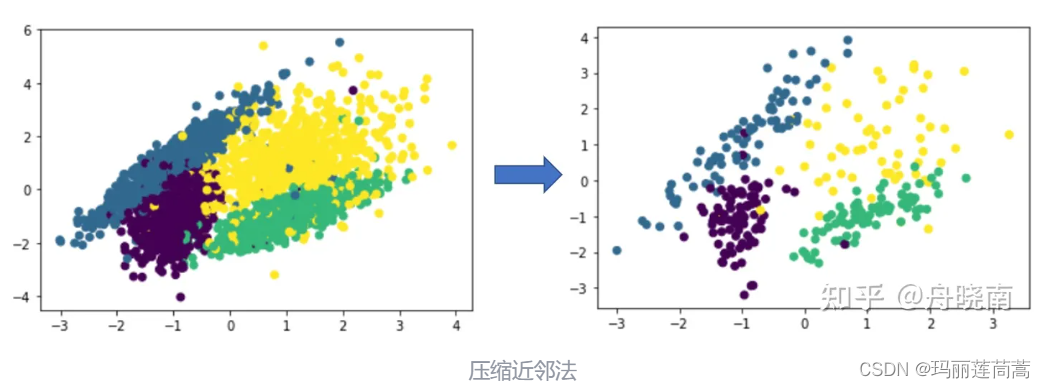
【Python代码】 剪辑法欠采样 CNN压缩近邻法欠采样
借鉴:关于K近邻(KNN),看这一篇就够了!算法原理,kd树,球树,KNN解决样本不平衡,剪辑法,压缩近邻法 - 知乎
一、剪辑法 当训练集数据中存在一部分不同类别数据的…
高级数据结构与算法 | 布谷鸟过滤器(Cuckoo Filter):原理、实现、LSM Tree 优化
文章目录 Cuckoo Filter基本介绍布隆过滤器局限变体 布谷鸟哈希布谷鸟过滤器 实现数据结构优化项Victim Cache备用位置计算半排序桶 插入查找删除 应用场景:LSM 优化 Cuckoo Filter
基本介绍 如果对布隆过滤器不太了解,可以看看往期博客:海量…
大数据技术之 Kafka
大数据技术之 Kafka 文章目录 大数据技术之 Kafka第 1 章 Kafka 概述1.1 定义1.2 消息队列1.2.1 传统消息队列的应用场景1.2.2 消息队列的两种模式 1.3 Kafka 基础架构 第 2 章 Kafka 快速入门2.1 安装部署2.1.1 集群规划2.1.2 集群部署2.1.3 集群启停脚本 2.2 Kafka 命令行操作…
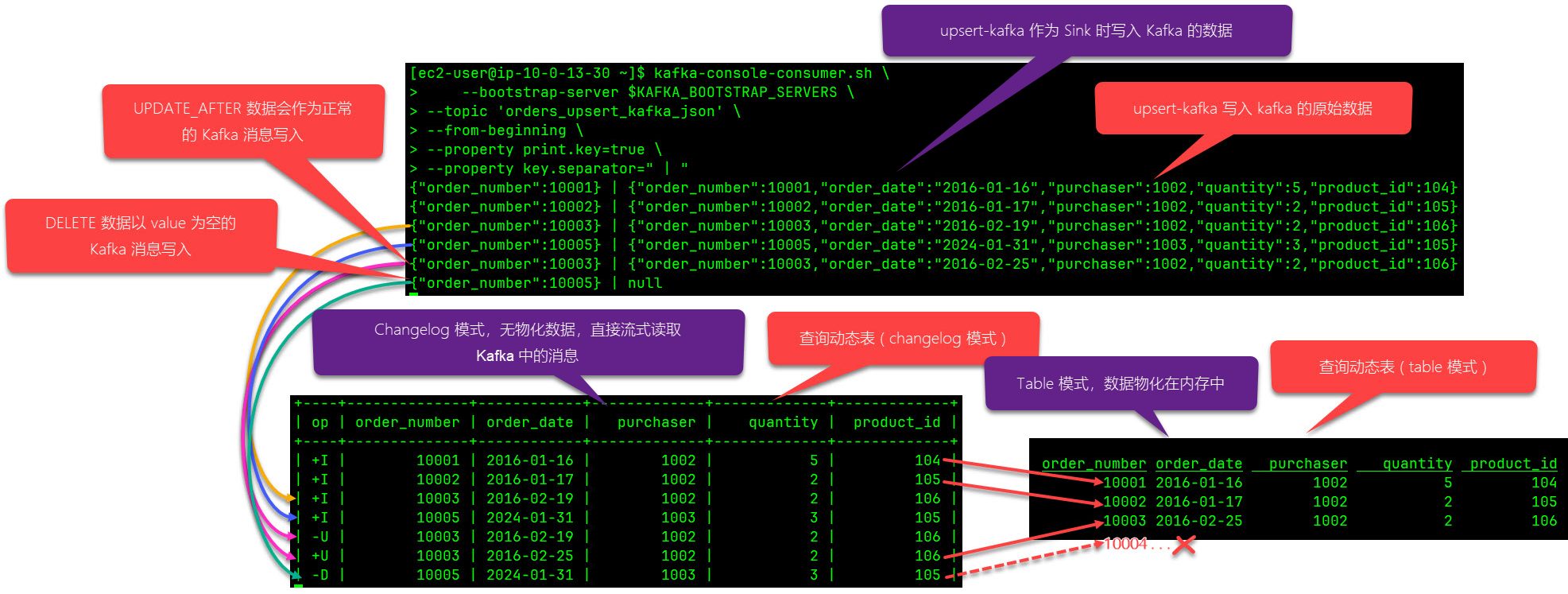
透彻理解实时数仓的支撑技术:Upsert Kafka 和 Flink 动态表(Dynamic Table)
博主历时三年精心创作的《大数据平台架构与原型实现:数据中台建设实战》一书现已由知名IT图书品牌电子工业出版社博文视点出版发行,点击《重磅推荐:建大数据平台太难了!给我发个工程原型吧!》了解图书详情,…