本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.ldbm.cn/p/37643.html
如若内容造成侵权/违法违规/事实不符，请联系编程新知网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
JavaWeb-Servlet服务连接器（三）
目录
Response响应对象
1.基本功能
2.重定向
3.路径
4.服务器输出数据到浏览器 Response响应对象
1.基本功能
设置响应行：格式为 HTTP/1.1 200 OK，可以使用 setStatus(int sc) 方法设置状态码为 200 表示成功。
方法名称描述setStatus(int sc)设…
Codeforces Round 892 (Div. 2) C. Another Permutation Problem 纯数学方法 思维题
Codeforces Round 892 (Div. 2) C. Another Permutation Problem 源码：
#include <iostream>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
#include <vector>
#include <stack>
#include &l…
鸿蒙剥离 AOSP 不兼容 Android 热门问题汇总，不吹不黑不吵
上周发了一篇 《鸿蒙终于不套壳了？纯血 HarmonyOS NEXT 即将到来》的相关资讯，没想到大家「讨（fa）论（xie）」的热情很高，莫名蹭了一波流量，虽然流量对我来说也没什么用，但…
什么是CSS的box-sizing属性？它有哪些取值，各有什么不同？
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ CSS的box-sizing属性⭐ 取值⭐ 不同之处⭐ 写在最后 ⭐ 专栏简介 前端入门之旅：探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅
欢迎来到前端入门之旅！这个专栏是为那些对Web…
安装cuda/cudann和pytorch
一、查看驱动信息 # 进入CMD输入命令
nvidia-smi 也可以右下角图标打开NVIDIA 设置进行查看 二、下载安装CUDA
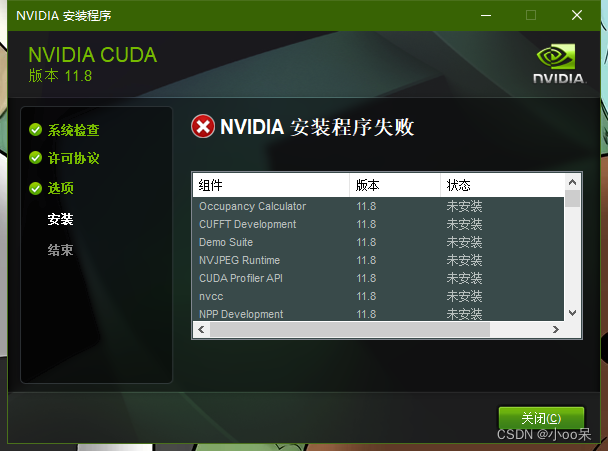
1、下载
下载地址 https://developer.nvidia.com/ 2、安装 推荐自定义安装。建议只勾选Cuda，只安装这一个就好，以免报错安装失败。 3、验证…
2023上半年京东奶粉行业品牌销售排行榜（京东数据分析平台）
近年来，受新生儿人口数量下降的影响，婴幼儿奶粉市场的需求量萎缩，市场由增量竞争转为存量竞争。根据鲸参谋电商数据分析平台的数据显示，今年上半年，京东婴幼儿奶粉市场的销量将近4400万，环比下降约19%&…
Qt中将信号封装在一个继承类中的方法
QLabel标签类对应的信号如下： Qt中标签是没有双击（double Click）这个信号的；
需求一：若想双击标签使其能够改变标签中文字的内容，那么就需要自定义一个“双击”信号，并将其封装在QLabel类的派生…
打造企业或者个人IP引流法
打造企业或者个人IP引流法.
大家好，我是百收网SEO编辑：狂潮老师，今天给大家分享企业IP打造的方法
首先我们想让人知道你的企业叫什么，怎么找到你的企业
这个时候我们就需要去各大平台发布信息，客户想了解直接去搜索…
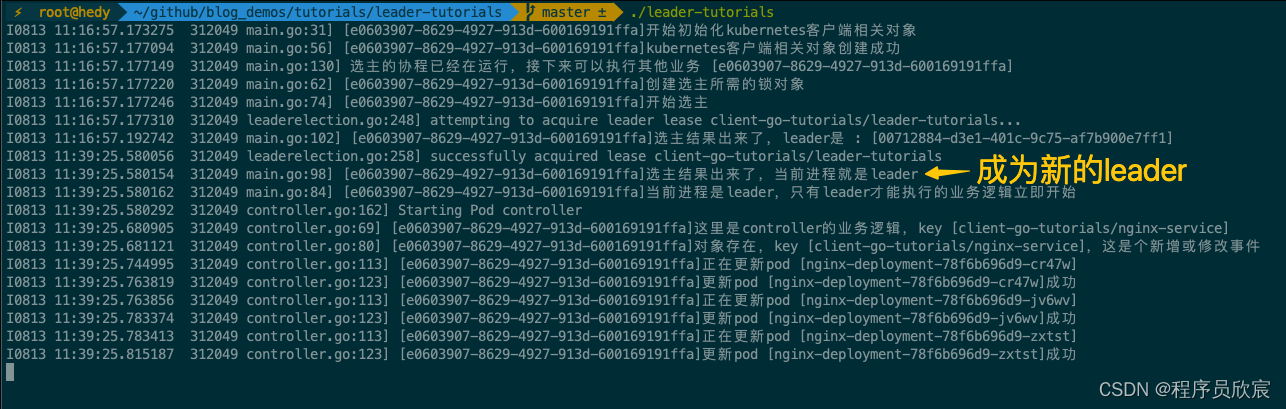
client-go实战之十二：选主(leader-election)
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码)：https://github.com/zq2599/blog_demos 本篇概览
本文是《client-go实战》系列的第十二篇，又有一个精彩的知识点在本章呈现：选主(leader-election)在解释什么是选主之前&…
善于用兵的人，军队粮草取自敌人
善于用兵的人，军队粮草取自敌人 【安志强趣讲《孙子兵法》第8讲】 【原文】 善用兵者，役不再籍，粮不三载；取用于国，因粮于敌，故军食可足也。 【注释】 役不再籍：役，兵役；…
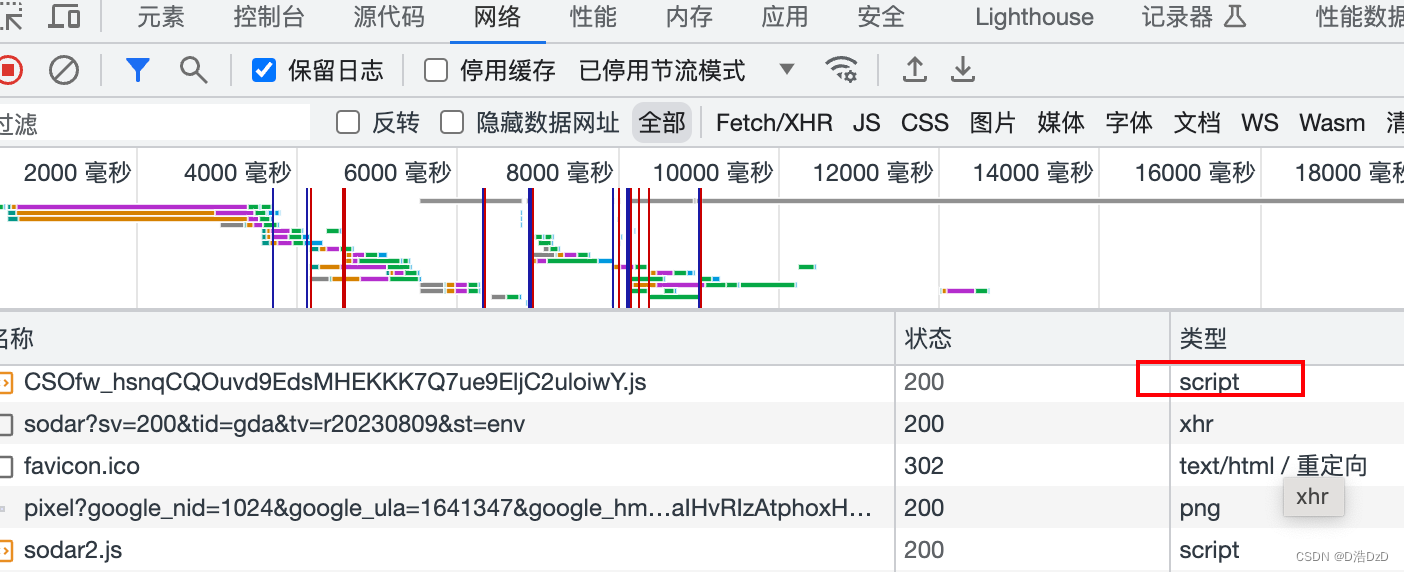
使用script标签解决跨域问题，但是只能使用get请求，且不需要获取get请求的数据，例如埋点，只需要触发后发送get请求，而不需要获取返回的参数
在项目中，使用埋点的时候，因为使用的是外部提供的接口，所以直接请求的时候，前端会报跨域的问题，本着不麻烦后端的想法，怎怎么前端实现跨域而完全不需要后段的配合，这时候就想到了通过script标签…
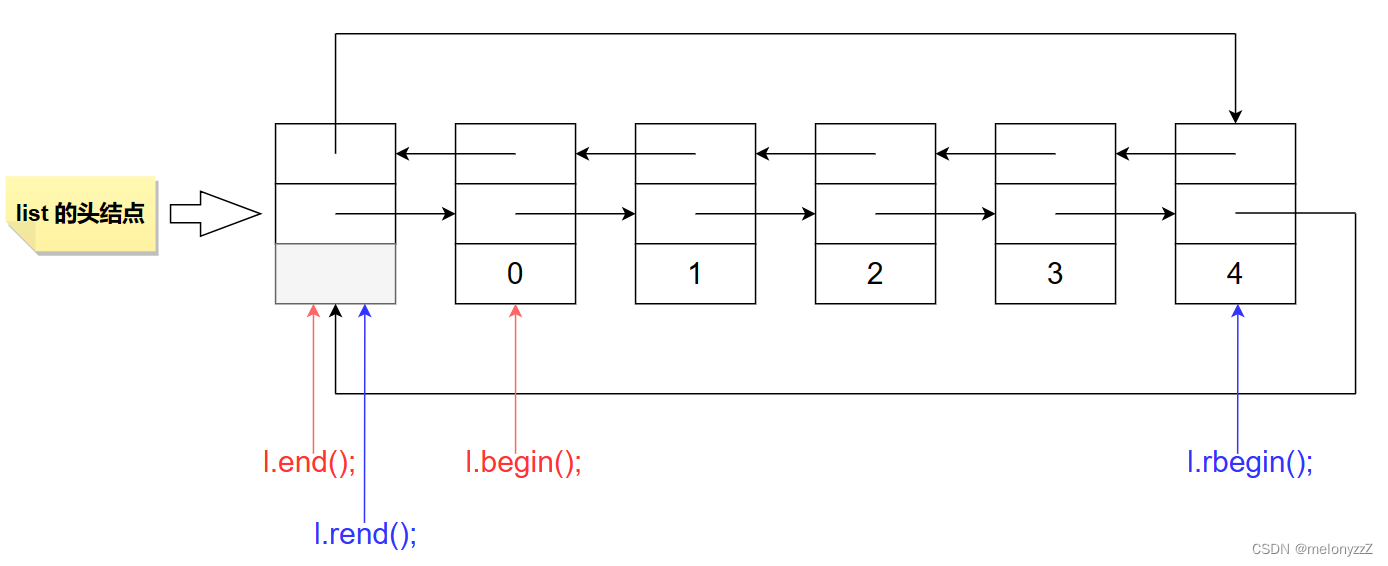
【C++ 学习 ⑬】- 详解 list 容器
目录
一、list 容器的基本介绍
二、list 容器的成员函数
2.1 - 迭代器
2.2 - 修改操作
三、list 的模拟实现
3.1 - list.h
3.2 - 详解 list 容器的迭代器
3.2 - test.cpp 一、list 容器的基本介绍
list 容器以类模板 list<T>（T 为存储元素的类型&…
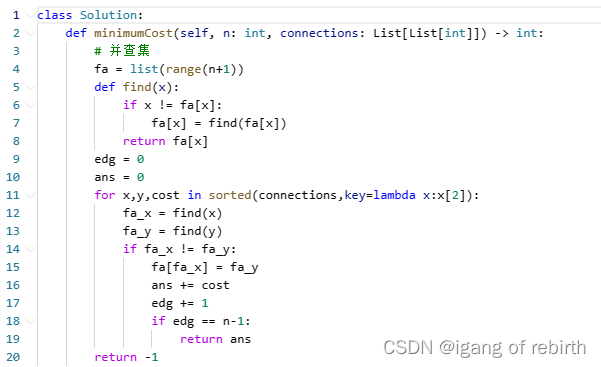
1216. 验证回文字符串 III；764. 最大加号标志；1135. 最低成本联通所有城市
1216. 验证回文字符串 III
核心思想：动态规划，这题需要一个思路的转换，删除最多k个字符判断是否为回文串，就相当于问你子序列中最长的回文串的长度是否比n-k长,就将这题转换为了最长回文子序列。 764. 最大加号标志
核心思想&am…
【TODO】米哈游20230813笔试第三题
是计算抽中什么当期五星的期望。 现在的程序结果是99.6087。结果不对，有时间再调。 #include <iostream>
#include <bits/stdc.h>
typedef long long LL;
using namespace std;int n 90;
double p;
// double min_p 1e-7;
double min_p 0.0000000000…
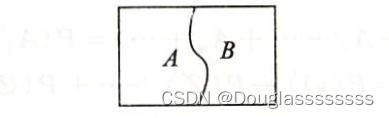
【考研数学】概率论与梳理统计 | 第一章——随机事件与概率（1）
文章目录 一、随机试验与随机事件1.1 随机试验1.2 样本空间1.3 随机事件 二、事件的运算与关系2.1 事件的运算2.2 事件的关系2.3 事件运算的性质 三、概率的公理化定义与概率的基本性质3.1 概率的公理化定义3.2 概率的基本性质 写在最后 一、随机试验与随机事件
1.1 随机试验 …
idea cannot download sources 解决方法
问题
点击class文件右上角下载源码失败
解决方案
找到idea terminal 控制台cd 至maven工程执行 mvn dependency:resolve -Dclassifiersources
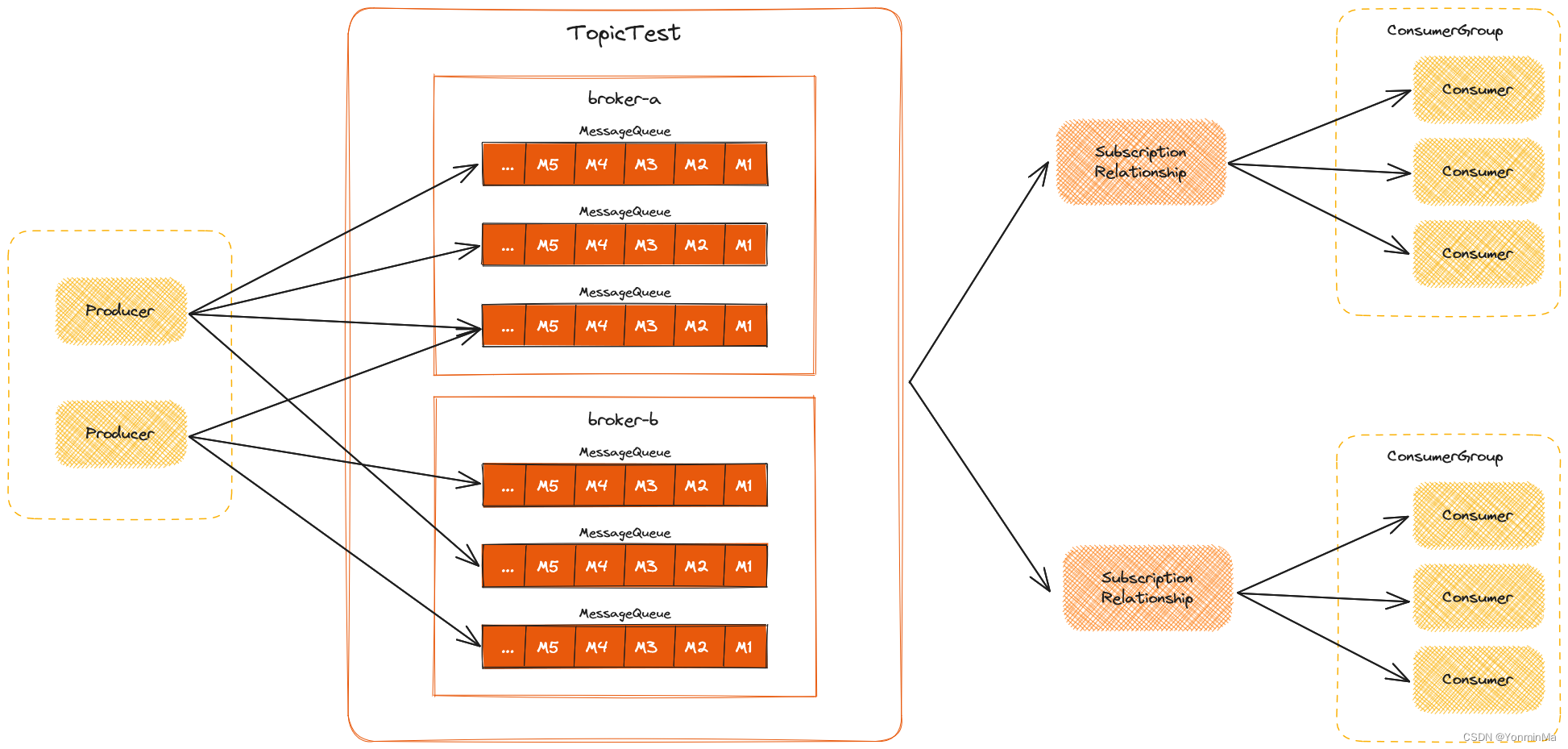
RocketMQ 5.1.0 源码详解 | Producer 发送流程
文章目录 初始化DefaultMQProducer实例发送流程DefaultMQProducer#sendDefaultMQProducerImpl#sendMQClientInstance#updateTopicRouteInfoFromNameServer使用特定 topic 获取路由信息使用默认 topic 获取路由信息 DefaultMQProducerImpl#sendDefaultImpl发送流程总结 初始化De…
Redisson实现锁以及redis缓存一致性问题
目录 RedissonClient实现最基本的锁
RedissonClient实现读写锁
RedissonClient实现闭锁
RedissonClient信号量
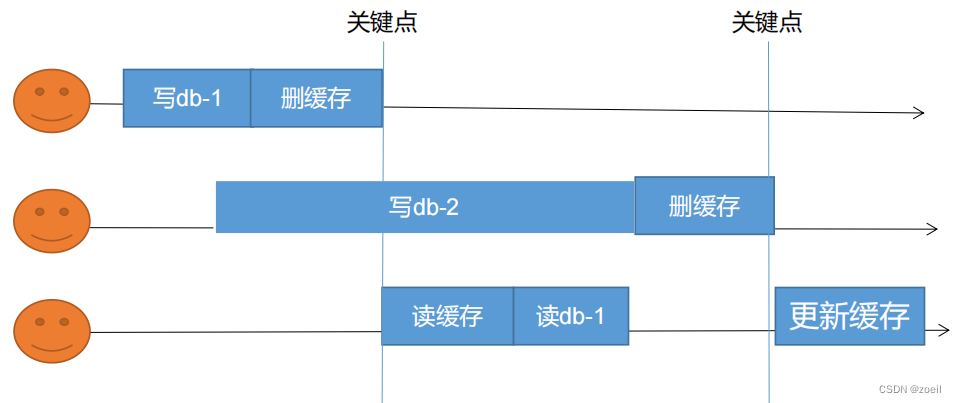
缓存不一致问题解决方案
一、双写模式
二、失效模式 RedissonClient实现最基本的锁 // 1、获取一把锁，只要锁的名字一样，就是同一把锁R…
![[Blender]Geometry nodes altermesh to UE](https://img-blog.csdnimg.cn/8d89e74a9e144cd1bcfbef5696695007.png)
[Blender]Geometry nodes altermesh to UE
首先要先下载插件
AlterMesh – Use geometry nodes inside Unreal
下载对应版本的插件后
打开UE，在对应的设置里面挂上blender.exe的路径 去官方下载一个Blender Geometry nodes 的示例 Demo Files — blender.org
贪心 二分查找和二分答案 递推与递归
贪心
知识点
局部最优解->整体最优解
贪心算法理论基础！_哔哩哔哩_bilibili
选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。
证明贪心策略的有效性 反证法 数学归纳法 例题
376.摆…