本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/429681.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
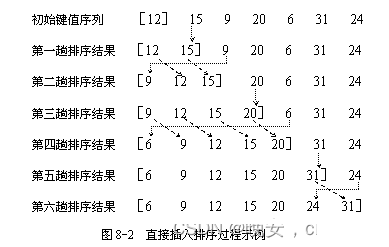
数据结构的直接插入排序(C语言版)
一.直接插入排序的基本概念
1.直接插入排序的基本思想 将数组分为已排序和未排序两部分。 每次从未排序部分取出一个元素,将其插入到已排序部分的合适位置,使得已排序部分保持有序。 重复步骤2,直到整个数组有序。
2.排序的工作原理 假设前 i-1 个元素已经有序,现在要将第…
电脑由于ntdll.dlI丢失导致exe崩溃有什么解决办法?解决ntdll.dll丢失问题
相信有一些用户正在面临一个叫做“ntdll.dll丢失”的问题,这种情况多半发生在试图运行某个程序时,系统会提示一条错误消息:“程序无法启动,因为计算机中丢失了ntdll.dll”。那么,为何ntdll.dll文件会丢失,又…
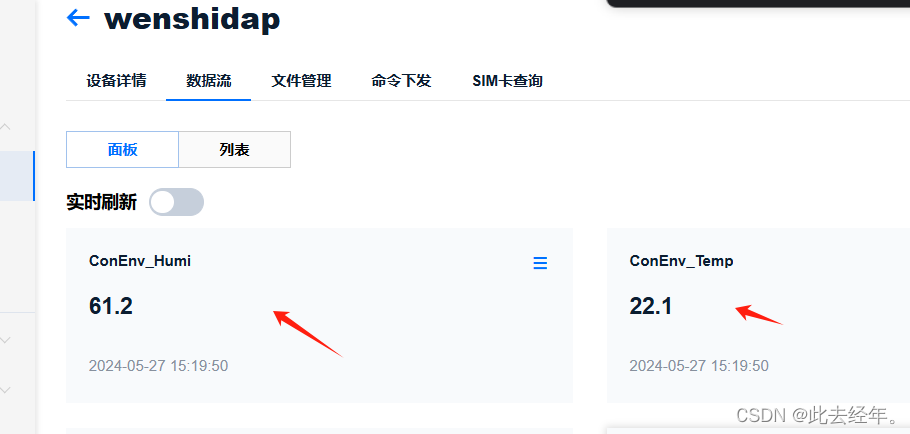
Python使用MQTT连接新版ONENet
Python MQTT 连接新版ONENet
简介
前几个教程我们使用mqtt.fx连接了新版的ONENet, 只是跑通了MQTT协议,但是在实际操作下还需要实现具体环境、具体设备的MQTT连接,本章教程将以Python MQTT的方式连接 ONENet
参考文档:
paho-mqtt PyPI
…
数据结构-二叉树系统性学习(四万字精讲拿捏)
前言 这里我会从二叉树的概念开始讲解,其次涉及到概念结构,以及堆的实现和堆排序。 目的是,堆比二叉树简单,同时堆本质上是二叉树的其中一种情况,堆属于二叉树顺序结构的实现 最后完善二叉树的讲解,也就是…
家用超声波清洗机哪个品牌好用?四款众人口口相传的品牌力荐
在追求极致清洁效果的今天,超声波清洗机以其高效、深入和温和的清洁能力,成为了众多行业乃至家庭用户的首选。不论是珍贵的珠宝首饰,精密的医疗器械,还是日常生活中的眼镜和手表,超声波清洗机都能够提供一种安全、快捷…
Java中Stack的使用详解
Stack是一种运算受限的线性表,其特点在于仅允许在表的一端(即表尾)进行插入和删除操作。这一端被称为栈顶,而相对的另一端则称为栈底。向一个栈插入新元素的操作称为进栈或入栈,它将新元素放到栈顶元素的上面ÿ…
DOS学习-目录与文件应用操作经典案例-type
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录
一.前言
二.使用
三.案例
1. 查看文本文件内容
2. 同时查看多个文本文件内容
3. 合并文…
spring boot 之 结合aop整合日志
AOP
该切面仅用于请求日志记录,若有其他需求,在此基础上扩展即可,不多逼逼,直接上代码。
引入切面依赖
<!-- 切面 -->
<dependency><groupId>org.springframework.boot</groupId><artifactId>sp…
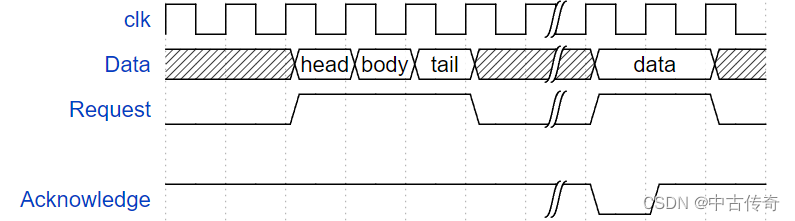
【Timimg Diagram--waveDorm】
ICer wave edit--waveDorm 1 Intro waveDorm2 Most often used2.1 The Signal2.2 Adding clock2.4 Add Spaces and Gaps 在ICer新入职之初,需要进行画波形图来进行理解、串讲和指导等目的; 最开始问我早入职一年的前辈,问她是怎么画的波形图&…
男士内裤什么材质的好?推荐男士内裤的注意事项
天气已经逐渐热了起来,广大男士们在夏天难免会出一身的汗,不少男士朋友都觉得一些吸湿性、透气性不好的内裤会在夏天穿着很不适,想挑选一些比较适合夏天的男士内裤,但现在的男士内裤品牌和材质分类却比较多,看得大家眼…
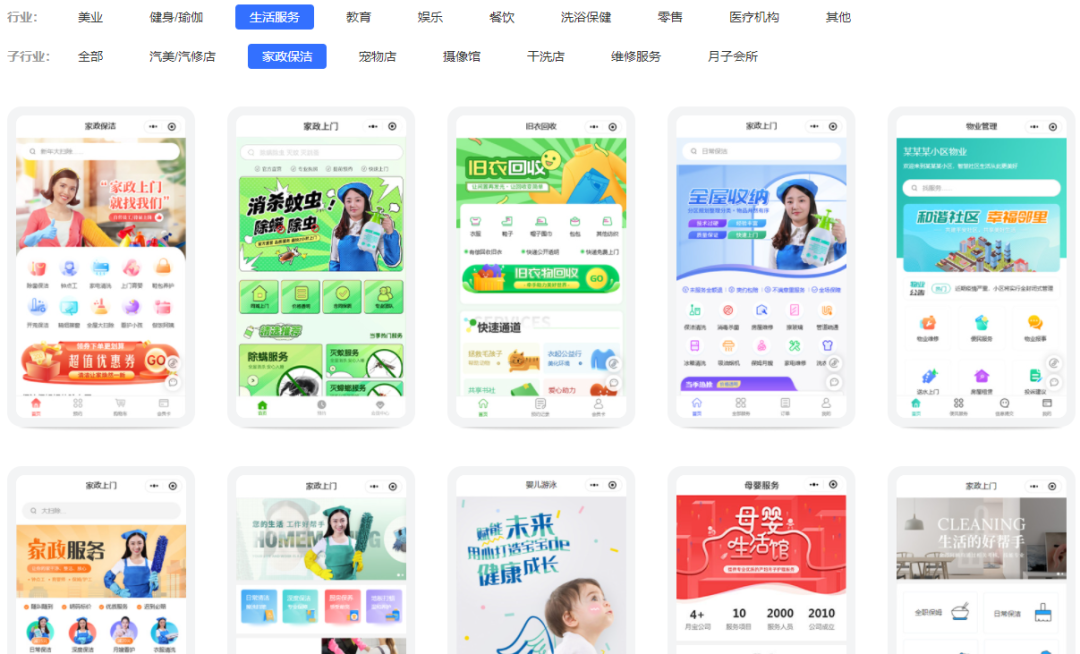
家政上门服务小程序,客商紧密连系的作用是什么
家政服务拓展速度很快,大小城市都有不少品牌门店,其涵盖项目多样化,使得部分年轻人和老年人长期消费需要,商家与客户都需要完善的路径进行长期合作。
运用【雨科】平台搭建家政上门服务预约小程序,客户随时预约服务、…
从三个维度把握习近平总书记关于基层治理的重要论述
基层强则国家强,基层安则天下安。党的十八大以来,习近平总书记围绕基层治理发表一系列重要论述,立意高远,内涵丰富,思想深刻,为新时代推进基层治理现代化提供了根本遵循和科学指南。习近平总书记关于基层治理的重要论述,科学运用马克思主义基本原理,立足我国国情、社情…
【译】MySQL 组复制 - 部分网络故障对性能的影响
原文地址:MySQL Group Replication – Partial Network Failure Performance Impact
在这个由两部分组成的博客系列中,我想介绍一些使用组复制的故障转移场景。在第一部分中,我将讨论我在撰写这些文章时发现的一种有趣的行为和性能下降。在第…
springboot 集成 es--未完结
基于es7.10.x版本
一、前提知识
常见的两种方式:spring boot提供的API 和 ES 官方提供的API ES官方: RestHighLevelClient: 适用于复杂、更细粒度控制的Elasticsearch 操作 spring boot: ElasticsearchRestTemplate:…
把握《中国共产党纪律处分条例》的鲜明特点
用严明的纪律管全党治全党是新时代全面从严治党的成功之举。新修订的《中国共产党纪律处分条例》(以下简称《条例》)是党的纪律的基础性法规,内容丰富、涉及面广、针对性强,同各级党组织和每一名党员息息相关。深刻领会《条例》的思想内涵、微言大义、内在逻辑,需要把握好…
selenium 爬取今日头条
由于今日头条网页是动态渲染,再加上各种token再验证,因此直接通过API接口获取数据难度很大,本文使用selenium来实现新闻内容爬取。
selenium核心代码
知识点:
代码中加了很多的异常处理,保证错误后重试,…
路由器交换机直连方案(RM50+RTL8367N)
不经过网口和变压器,实现板级网口扩展。
通过网口,网线连接 板级芯片直接连接,验证OK 激光导航控制板通过路由器上网成功
AI应用案例:AI就是这么牛,聊天就能分析股票。
今天给大家介绍一个可能跟你切身相关的案例“大模型股票分析“!首先申明这不是教你怎么炒股的方法,而是告诉你可以通过AI协助你去分析股票。 像我是程序员出身,有数据给我,我可以写SQL语句查数据库,或者通过写代码来分…
![二维前缀和[模版]](https://img-blog.csdnimg.cn/direct/9ea5fd5df1204ece952d5d5523a6a4fd.png)