本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/430368.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
这些趣味科学小故事,让孩子从小爱上数理化,快收藏!
在我们的日常生活中,无论是洗碗时看到的泡沫,还是在公园里看到的彩虹,背后都隐藏着无数的科学奥秘。这些现象虽然看似平常,却都深深扎根于数理化的基本原理中。生活中一些常见的问题,也能通过转化成数理化的问题来解决。那么在现实生活中,数理化是如何帮助我们解决问题的…
专家解读 | NIST网络安全框架(2):核心功能
NIST CSF是一个关键的网络安全指南,不仅适用于组织内部,还可帮助管理第三方网络安全风险。CSF核心包含了六个关键功能——治理、识别、保护、检测、响应和恢复,以及与这些功能相关的类别和子类别。本文将深入探讨CSF核心的主要内容࿰…
对象解构与迭代器的猫腻?
前言
变量的解构赋值是前端开发中经常用到的一个技巧,比如:
// 对象解构
const obj { a: 1, b: 2 };
const { a, b } obj;
console.log(a, b)数组解构
const arr [1, 2, 3];
const [a, b] arr;
console.log(a, b)工作中我们最经常用的就是类似上面…
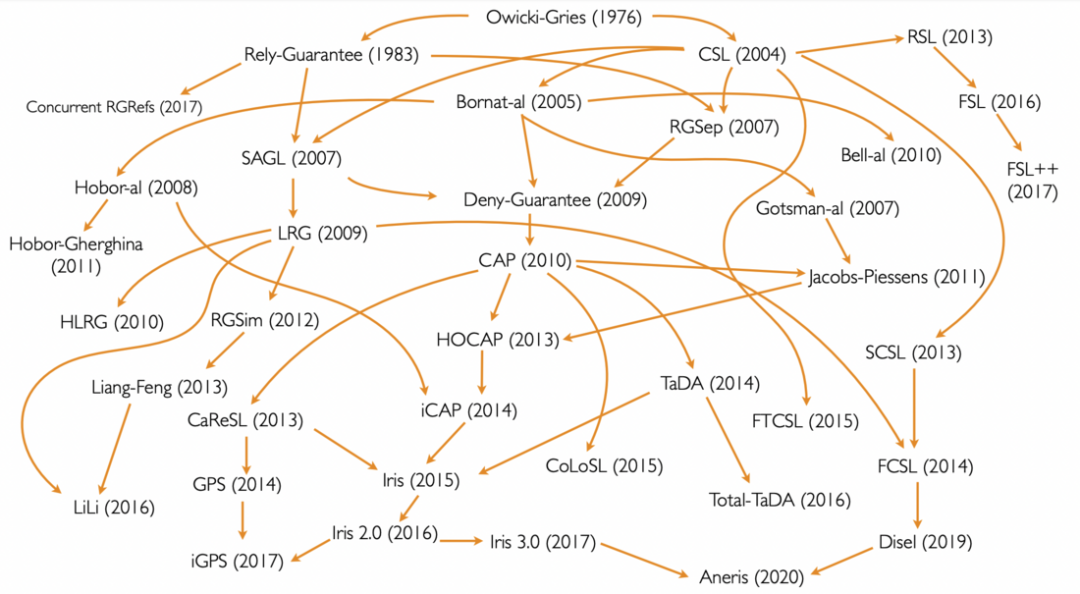
【Rust日报】Rust 中的形式验证
文章 - 未来的愿景:Rust 中的形式验证 这篇文章回顾了形式化验证的基本概念,作者展示了如何使用 Hoare triples 来描述和推理程序的正确性,以及如何使用分离逻辑来解决验证的复杂性。文章还解释了为什么 Rust 适用于形式化验证,以…
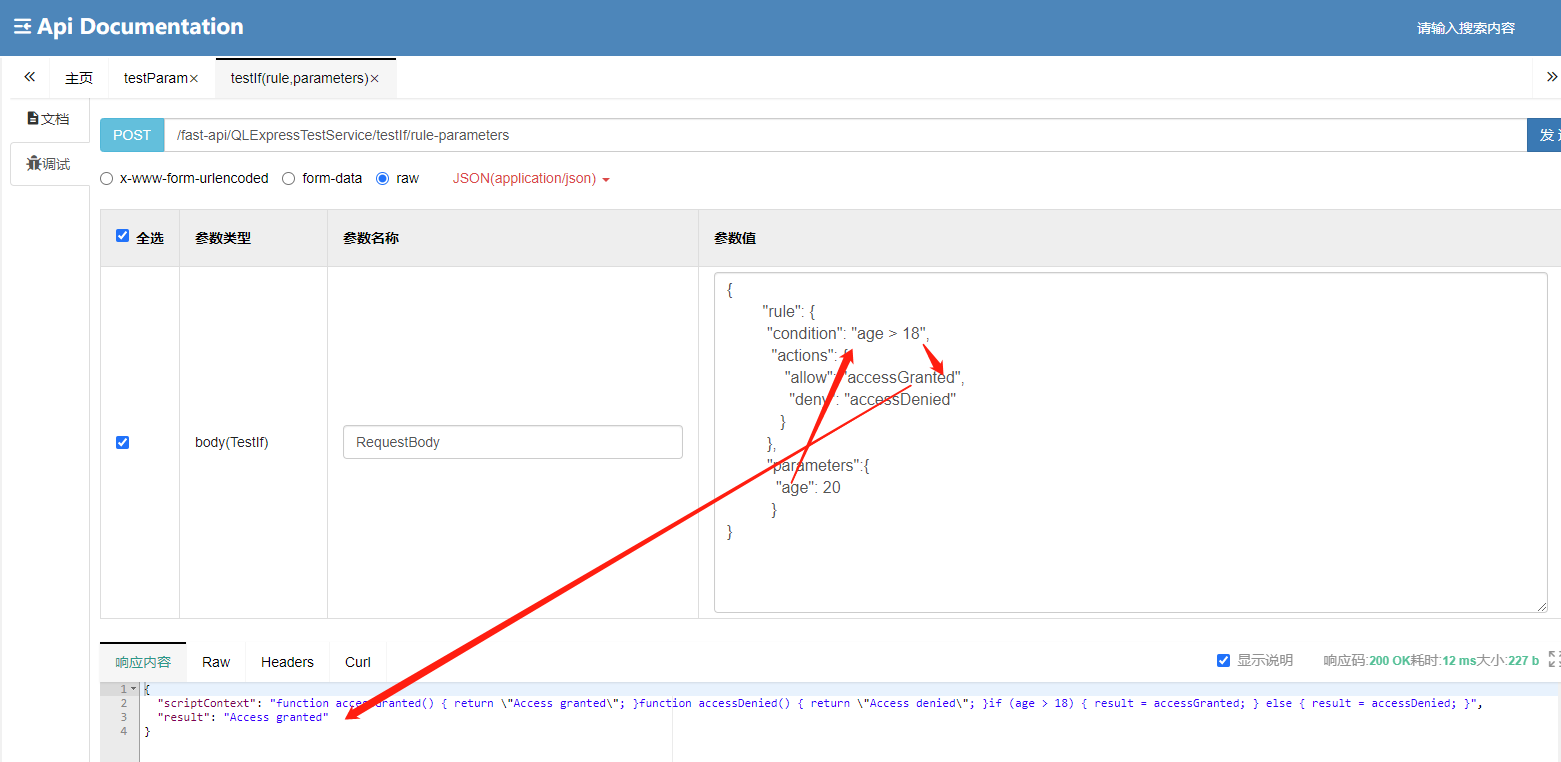
QLExpress入门及实战总结
文章目录 1.背景2.简介3.QLExpress实战3.1 基础例子3.2 低代码实战3.2.1 需求描述3.2.1 使用规则引擎3.3.2 运行结果 参考文档 1.背景
最近研究低代码实现后端业务逻辑相关功能,使用LiteFlow作为流程编排后端service服务, 但是LiteFlow官方未提供图形界面编排流程。…
vue3(一):Vue3简介、创建vue3工程、Vue3中的响应式
目录
一.Vue3简介
1.性能提升
2.源码升级
3.拥抱ts
4.新特性
(1)Composition API(组合API):
(2)新的内置组件:
(3)其他改变:
二.创建vue…
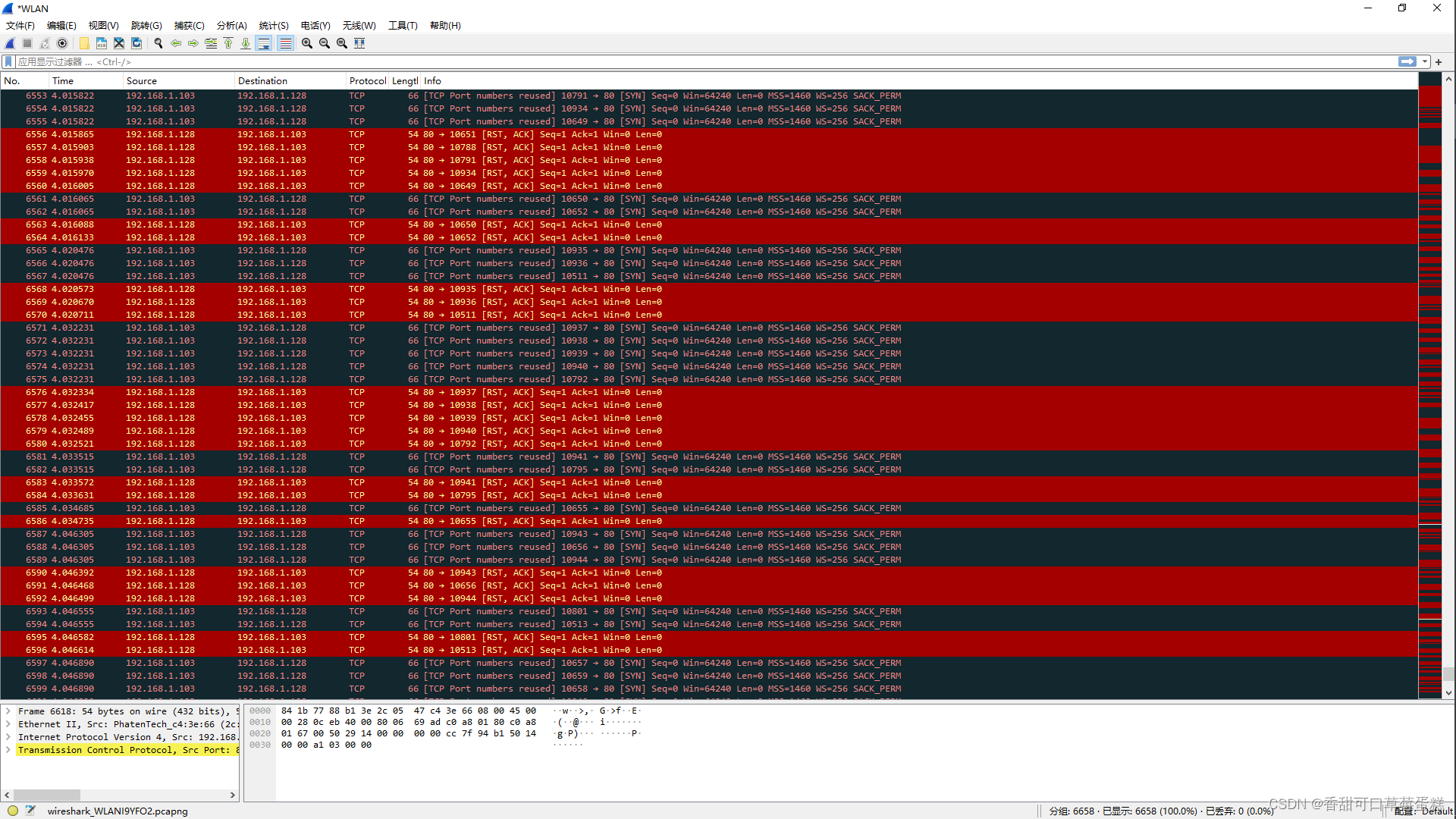
基于 IP 的 DDOS 攻击实验
一、介绍
基于IP的分布式拒绝服务(Distributed Denial of Service, DDoS)攻击是一种利用大量受控设备(通常是僵尸网络)向目标系统发送大量请求或数据包,以耗尽目标系统的资源,导致其无法正常提供服务的攻击…
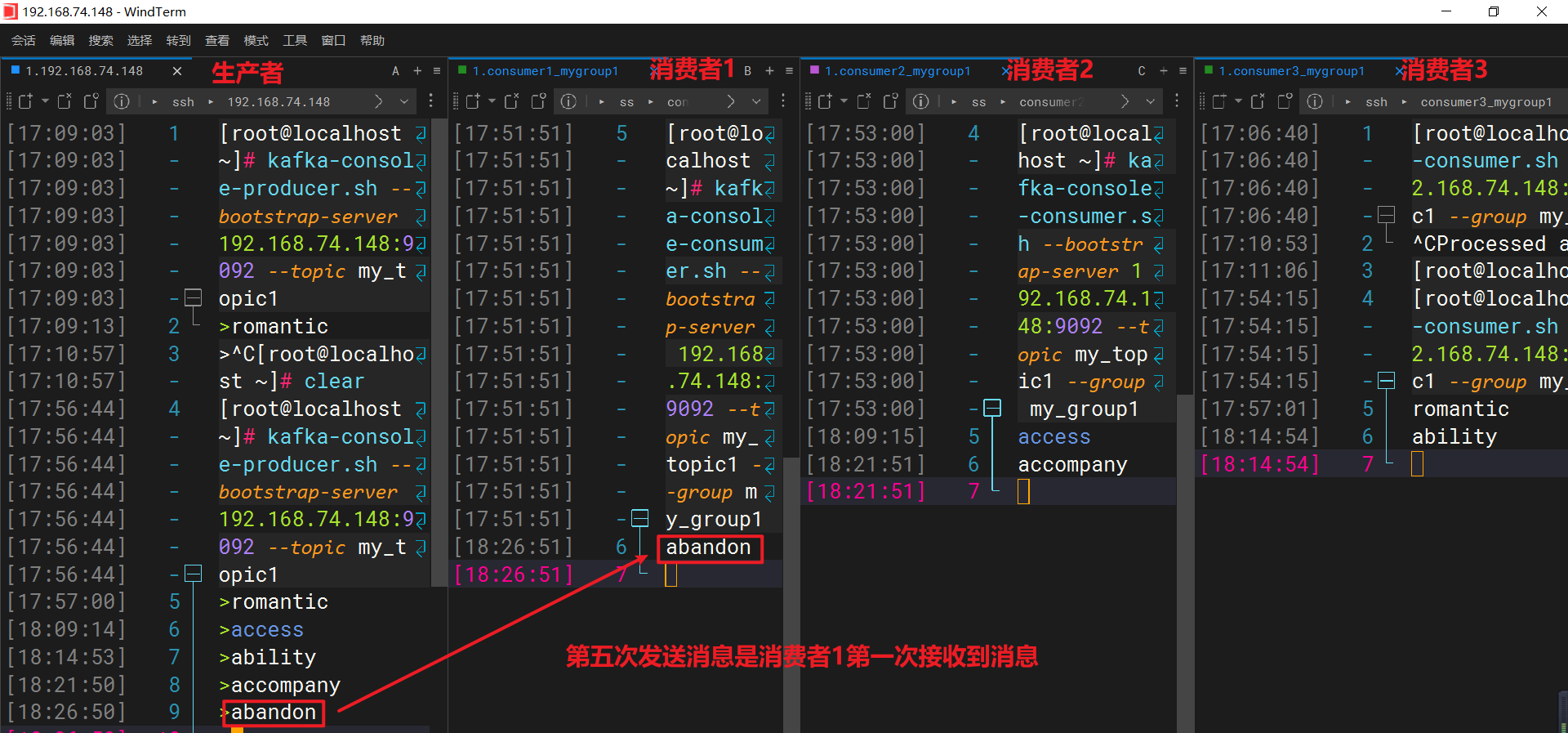
kafka-消费者组-点对点测试
文章目录 1、点对点测试1.1、获取 kafka-consumer-groups.sh 的帮助信息1.2、列出所有的 消费者组1.3、创建消费者1并指定组 my_group11.4、创建消费者2并指定组 my_group11.5、创建消费者3并指定组 my_group11.6、创建生产者发送消息到 my_topic1 主题1.6.1、发送第一条消息ro…
docker-compose 映射端口失败! docker端口映射失败 ,docker映射只能使用老端口,映射无法使用
1. 现象 使用docker-compose 启动项目,发现映射端口出现问题,不能映射端口! 如图: 使用原来端口是可以使用的 2. 问题原因: 使用了docker-mode 为host模式,所以不能换端口,只能写为"8086:…
1.Redis之初识Redis分布式系统
1.初识Redis
1.1 官网
Redis中文网
Redis 教程 | 菜鸟教程 (runoob.com)
1.2 解释
在内存中存储数据
定义变量,不就是在内存中存储数据嘛??
Redis 是在分布式系统(进程的隔离性:Redis 就是基于网络,可以把自己内存中的变量给别的进程…
Big Demo Day第十三期活动即将启幕,Web3创新项目精彩纷呈,PEPE大奖等你抽取
5月28号在香港数码港 Big Demo Day第十三期 活动即将拉开帷幕,活动将汇集众多Web3领域的创新项目,为参会者带来一场科技与智慧交融的盛宴。在这里,你不仅能深入了解区块链、AI等前沿技术的最新应用,还能有机会赢取丰厚的PEPE大奖。…
matplotlib ---词云图
词云图是一种直观的方式来展示文本数据,可以体现出一个文本中词频的使用情况,有利于文本分析,通过词频可以抓住一篇文章的重点 本文通过处理一篇关于分析影响洋流流向的文章,分析影响洋流流向的主要因素都有哪些
文本在文末结尾 …
第十三届蓝桥杯国赛大学B组填空题(c++)
A.2022 动态规划 AC;
#include<iostream>
#define int long long
using namespace std;
int dp[2050][15];
//dp[i][j]:把数字i分解为j个不同的数的方法数
signed main(){dp[0][0]1;for(int i1;i<2022;i){for(int j1;j<10;j){//一种是已经分成j个数,这时只需每一个…
The Sandbox 和 Bitkub 联手增强东南亚元宇宙中心
作为去中心化游戏虚拟世界和区块链平台的先驱,The Sandbox 正与泰国领先的区块链网络 Bitkub Blockchain Technology Co., Ltd. 展开创新合作。双方合作的目的是将Bitkub元宇宙的影响力扩展到The Sandbox,建立一个元宇宙中心,向用户承诺从 Bi…
如何在OrangePi AIpro智能小车上实现安全强化学习算法
随着人工智能和智能移动机器人的广泛应用,智能机器人的安全性和高效性问题受到了广泛关注。在实际应用中,智能小车需要在复杂的环境中自主导航和决策,这对算法的安全性和可靠性提出了很高的要求。传统的强化学习算法在处理安全约束时存在一定…
Mesa软件框架以及重要数据结构分析
Mesa软件框架以及重要数据结构分析 引言 Mesa的实现比较复杂,其中还有许多的数据结构之间的关系逻辑还不是很清楚。感觉分析了又没有分析一样,这里我们再理一理! 1.1 Mesa下EGL/GL核心数据结构和层级关系 MESA的核心数据结构很多很复杂&#…
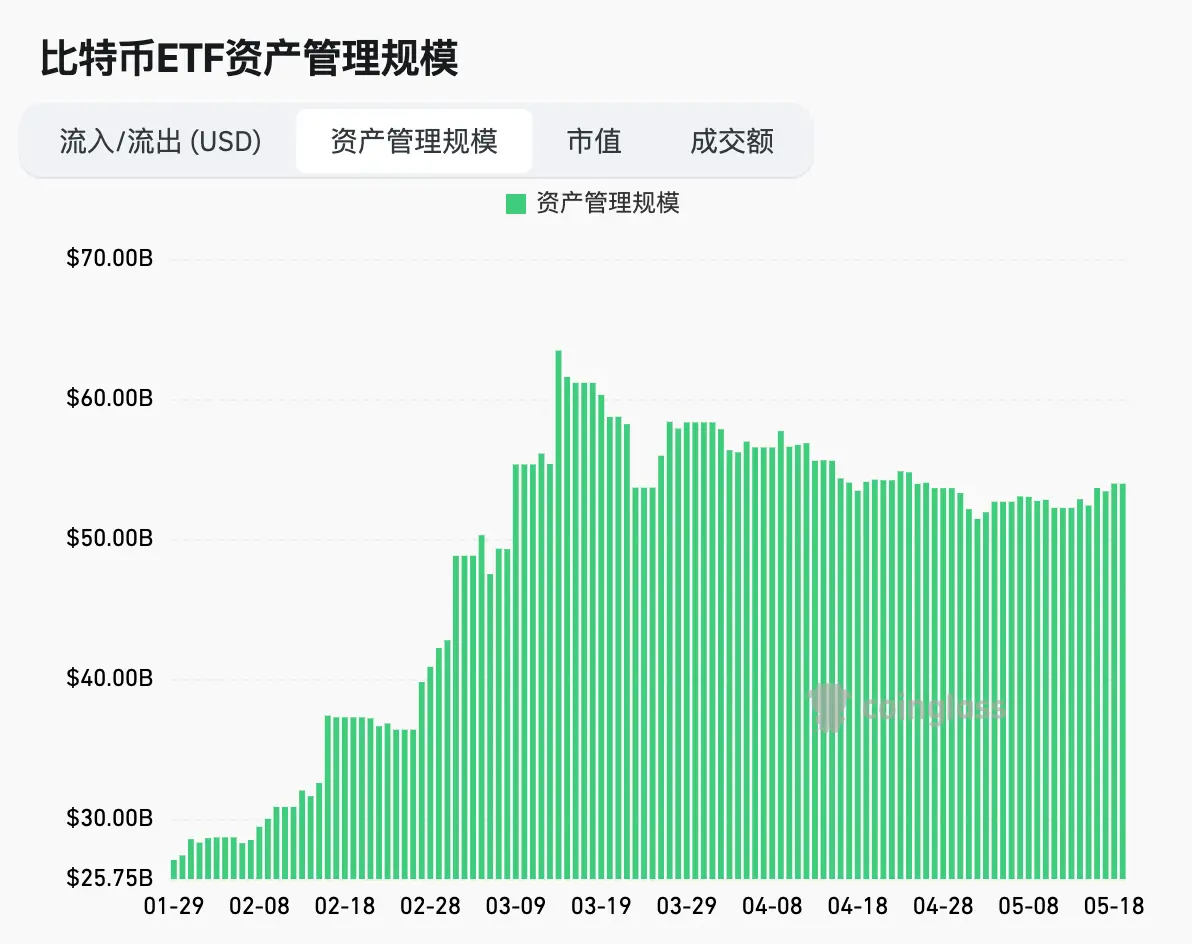
Hotcoin Research | 市场洞察:2024年5月13日-5月19日
加密货币市场表现 目前,加密货币总市值为1.32万亿,BTC占比54.41%。
本周行情呈现震荡上行的态势,BTC在5月15日-16日,有一波大的拉升,周末为震荡行情。BTC现价为67125美元。
上涨的主要原因:美国4月CPI为3…
中国新能源产业助推全球绿色发展
中国车企长城汽车旗下电动汽车品牌欧拉好猫1月12日在泰国罗勇新能源汽车制造基地正式下线,这是泰国本土生产的第一款量产纯电动汽车。图为工人在生产车间内工作。新华社发【中国经济亮色与世界发展机遇】在绿色发展理念指引下,中国新能源产业通过多年自主技术创新、供应链整合…
软件架构设计之质量属性浅析
引言
在数字化浪潮席卷而来的今天,软件已经渗透到我们生活的方方面面,从手机APP到大型企业级系统,无一不彰显着软件技术的魅力。然而,在这背后,软件架构设计作为软件开发的基石,其质量属性的重要性不言而喻…