本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/430541.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
数据库之Mysql提权
MySQL UDF 提权
UDF(user defined function)⽤户⾃定义函数,是 mysql 的⼀个拓展接⼝。⽤户可以通过⾃定义函数实现在mysql中⽆法⽅便实现的功能,其添加的新函数都可以在 sql 语句中调⽤,就像调⽤本机函数⼀样。 先前…
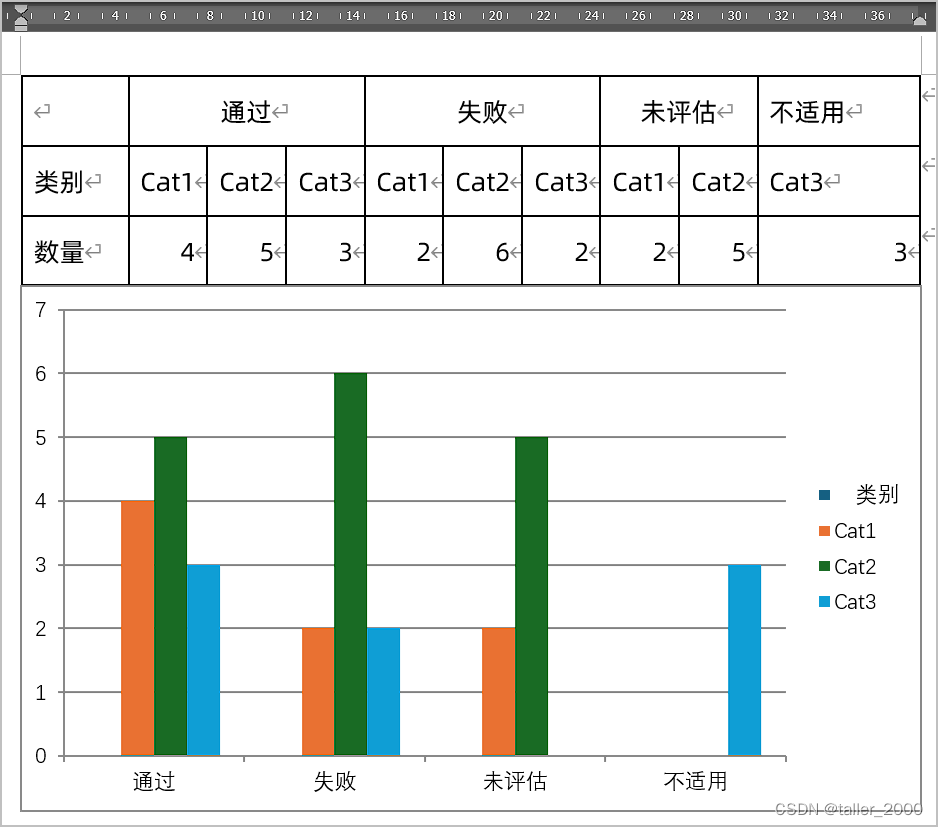
使用Word表格数据快速创建图表
实例需求:Word的表格如下所示,标题行有合并单元格。 现在需要根据上述表格数据,在Word中创建如下柱图。如果数据在Excel之中,那么创建这个图并不复杂,但是Word中就没用那么简单了,虽然Word中可以插入图表&a…
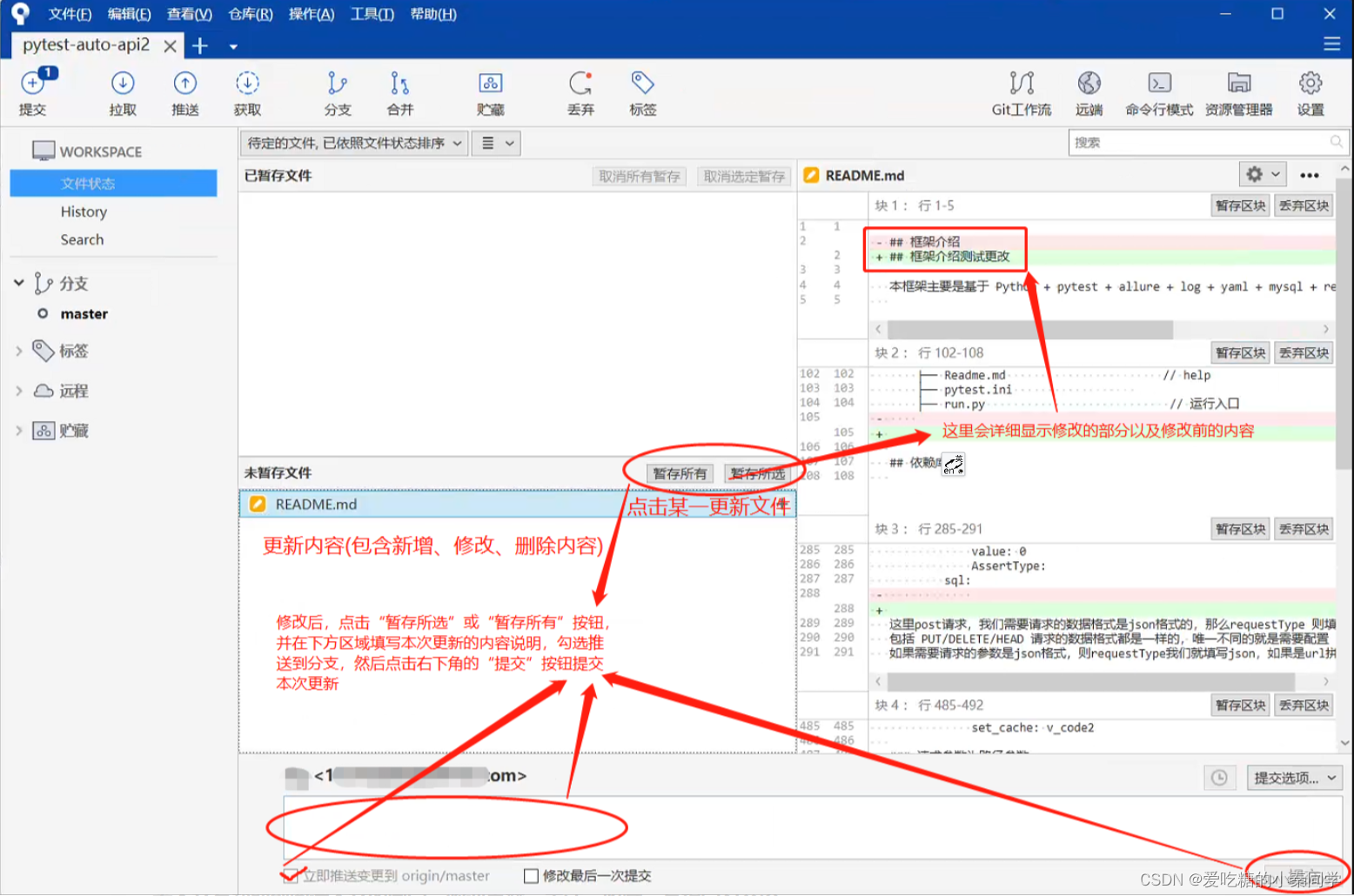
Sourcetree安装教程及使用
1 Sourcetree介绍 Sourcetree是一款免费的Git图形化客户端,它由Atlassian开发,提供了跨平台的支持,可运行在Windows和Mac操作系统上。Sourcetree可以让开发者更方便地使用Git来管理代码,不需要在命令行中输入复杂的Git命令&#x…
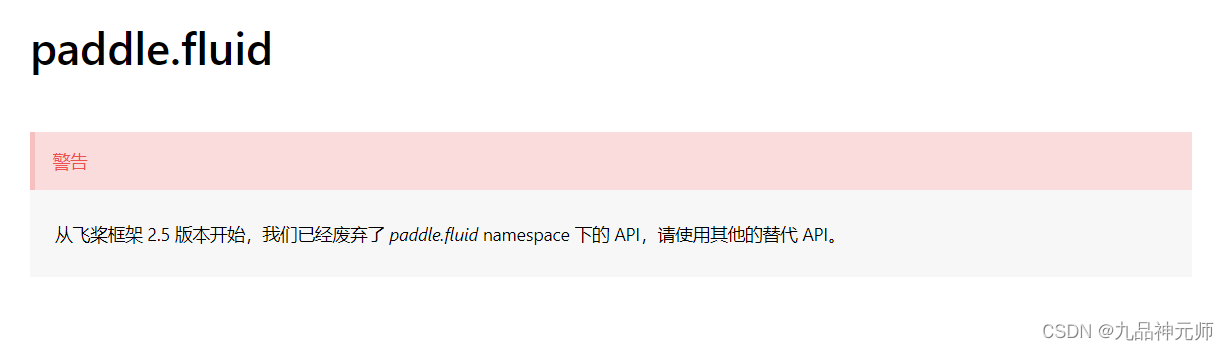
Paddle使用问题No module named ‘paddle.fluid’
这是Paddle版本的问题,从飞桨框架 2.5 版本开始,已经废弃了 paddle.fluid 。
解决方案:修改paddle版本
pip install paddlepaddle2.4.0
牛客热题:数据流中的中位数
📟作者主页:慢热的陕西人 🌴专栏链接:力扣刷题日记 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 文章目录 牛客热题:数据流中的中位数题目链接方法一…
Python--List列表
list列表⭐⭐ 1高级数据类型 Python中的数据类型可以分为:数字型(基本数据类型)和非数字型(高级数据类型) ●数字型包含:整型int、浮点型float、布尔型bool、复数型complex ●非数字型包含:字符…
【微服务】springboot 构建docker镜像多模式使用详解
目录 一、前言
二、微服务常用的镜像构建方案
3.1 使用Dockerfile
3.2 使用docker plugin插件
3.3 使用docker compose 编排文件
三、环境准备
3.1 服务器
3.2 安装JDK环境
3.2.1 创建目录
3.2.2 下载安装包
3.2.3 配置环境变量
2.2.4 查看java版本
3.3 安装maven …
STM32定时器及输出PWM完成呼吸灯
文章目录 一、STM32定时器原理1、基本定时器2、通用定时器(1)时钟源(2)预分频器PSC(3)计数器CNT(4)自动装载寄存器ARR 3、高级定时器 二、PWM工作原理三、控制LED以2s的频率周期性地…
(超详细)字符函数和字符串函数【上】
前言 C 语言中对字符和字符串的处理很是频繁,但是 C 语言本身是没有字符串类型的,字符串通常放在 常量字符串 中或者 字符数组 中。 字符串常量 适用于那些对它不做修改的字符串函数 . 1.求字符串长度函数
strlen函数
我们要求一个字符串函数的长度…
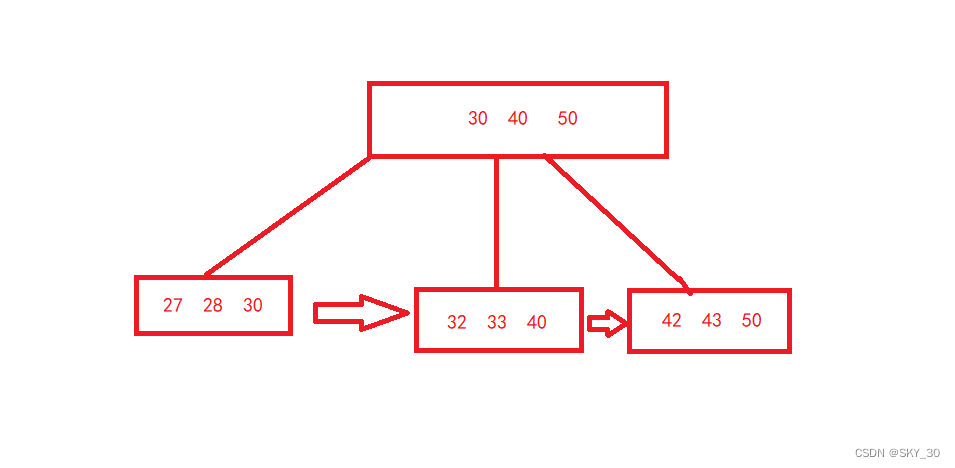
【数据库基础-mysql详解之索引的魅力(N叉树)】
索引的魅力目录 🌈索引的概念🌈使用场景🌈索引的使用🌞🌞🌞查看MySQL中的默认索引🌞🌞🌞创建索引🌞🌞🌞删除索引 站在索引背后的那个男…
深入解析 JSONPath:从入门到精通
码到三十五 : 个人主页 在数据处理和交换领域,JSON已经成为了一种广泛使用的数据格式, 如何有效地查询和操作这些数据也变得越来越重要。在这种情况下,JSONPath 应运而生,成为了一种在JSON数据中定位和提取信息的强大工…
手机投屏技巧:手机怎么投屏到电脑显示屏上?精选6招解决!
手机怎么投屏到电脑显示屏上?出于一些不同的原因,大多数人都希望能将手机投屏到电脑上。其中一个常见的原因是,大家经常会希望在笔记本电脑上共享图片,而无需上传或者登录微信进行文件传输。以及希望不依靠投影仪,就能…
Google使用AI改进了 Sheets;开源视觉语言模型llama3v;开源情绪语音模型ChatTTS;
✨ 1: Google has improved Sheets with AI.
Google 使用 AI 改进了 Sheets 您可以使用 Gemini 处理您的数据并将其变成老师。
优化您的数据
Gemini 了解您的数据并提出改进建议。
例如,它可以将重复数据转换为更实用的下拉框。
解释数据
通过单击双子座图标…
九章云极DataCanvas公司重磅亮相第七届数字中国建设峰会
近日,由国家发展改革委、国家数据局、国家网信办、科技部、国务院国资委、福建省人民政府共同主办的第七届数字中国建设峰会在福州盛大举行,九章云极DataCanvas公司重磅亮相峰会现场,深度展示智算中心建设核心成果及“算法算力”一体化AI智算…
使用python绘制一个五颜六色的爱心
使用python绘制一个五颜六色的爱心 介绍效果代码 介绍
使用numpy与matplotlib绘制一个七彩爱心!
效果 代码
import numpy as np
import matplotlib.pyplot as plt# Heart shape function
def heart_shape(t):x 16 * np.sin(t)**3y 13 * np.cos(t) - 5 * np.cos…
Day 6:2981. 找出出现至少三次的最长特殊子字符串 I
Leetcode 2981. 找出出现至少三次的最长特殊子字符串 I 给你一个仅由小写英文字母组成的字符串 s 。 如果一个字符串仅由单一字符组成,那么它被称为 特殊 字符串。例如,字符串 “abc” 不是特殊字符串,而字符串 “ddd”、“zz” 和 “f” 是特…
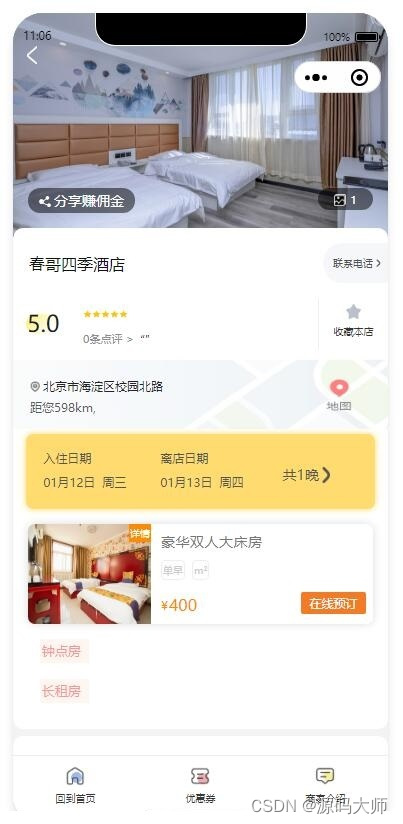
酒店提前线上订房小程序源码系统 PHP+MySQL组合开发 源码开源可二开 带完整的安装代码包以及搭建教程
系统概述
随着移动互联网的普及,越来越多的人习惯通过手机进行酒店预订。传统的线下订房方式逐渐无法满足用户的需求,酒店提前线上订房小程序的出现成为必然趋势。该源码系统的开发旨在为酒店提供一个便捷、高效的线上订房平台,提升用户体验…
JAVA:Random详解
Java中的java.util.Random类用于生成伪随机数。它提供了多种方法来生成不同类型的随机数,包括整数、浮点数和布尔值。以下是对Random类及其主要方法的详细介绍 一、生成随机数
创建一个Random对象,可以使用以下两种方式: 无参构造函数&…
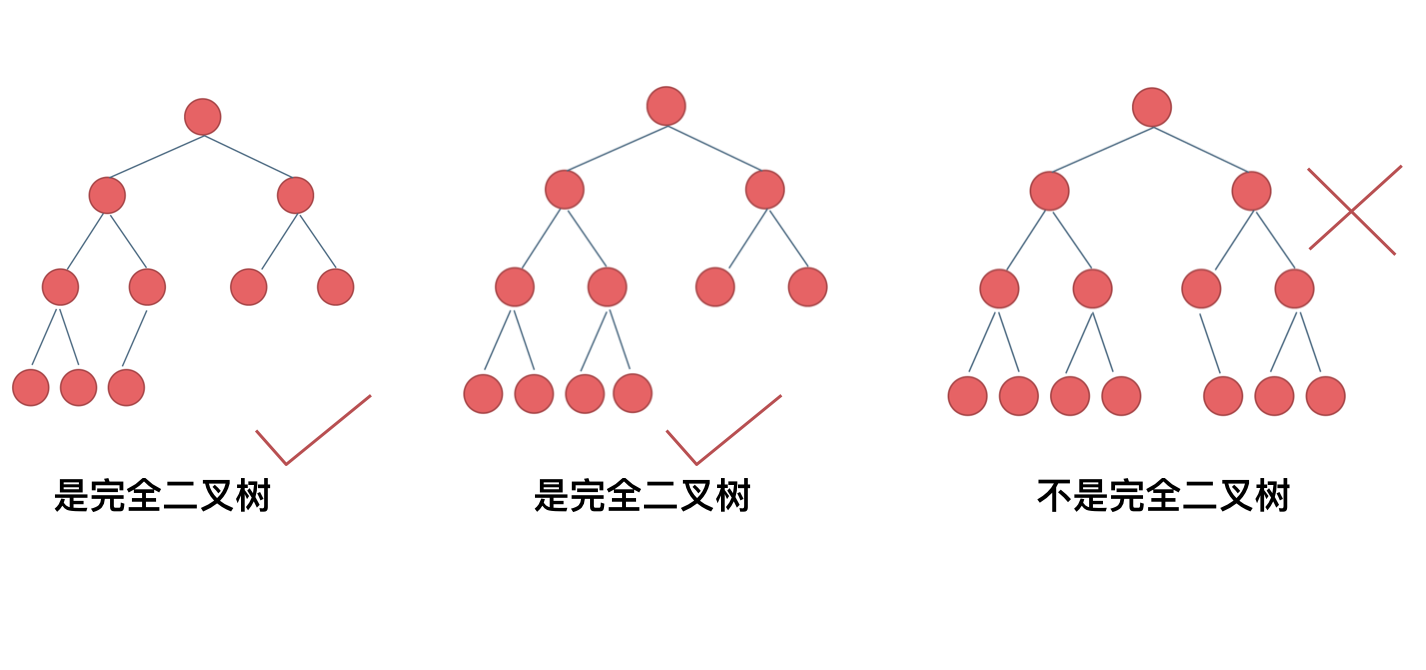
222.完全二叉树的节点个数
给出一个完全二叉树,求出该树的节点个数。
示例 1:
输入:root [1,2,3,4,5,6]输出:6
示例 2:
输入:root []输出:0
示例 3:
输入:root [1]输出:1
提示…