本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/440889.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
大模型api谁家更便宜
1 openai
可点此链接查询价格:https://openai.com/api/pricing/ 2 百度
可点此链接查询价格:https://console.bce.baidu.com/qianfan/chargemanage/list 需要注意,百度千帆平台上还提供其他家的模型调用服务, 如llama, yi-34b等…
NISP 一级 | 3.3 网络安全防护与实践
关注这个证书的其他相关笔记:NISP 一级 —— 考证笔记合集-CSDN博客 0x01:虚拟专用网络 VPN 概述
虚拟专用网络(Virtual Private Network,VPN)是在公用网络上建立专用网络的技术。整个 VPN 网络的任意两个节点之间的连…
Deploying Spring Boot Apps Tips
Java PaaS providers chatter command Efficient deployments See also
spring-boot-reference.pdf https://docs.spring.io/spring-framework/reference/integration/checkpoint-restore.html
Elasticsearch-数据迁移elasticdump
一、环境信息
主机名 IPelasticsearch-master10.10.10.1elasticsearch-slave10.10.10.2 二、互联网部分
2.1、Nodejs下载安装(master节点)
#官网:Download | Node.js #下载nodejs包 [rootelasticsearch-master home]# wget -c htt…
一文搞定高并发编程:CompletableFuture的supplyAsync与runAsync
CompletableFuture是Java 8中引入的一个类,用于简化异步编程和并发操作。它提供了一种方便的方式来处理异步任务的结果,以及将多个异步任务组合在一起执行。CompletableFuture支持链式操作,使得异步编程更加直观和灵活。 在引入CompletableFu…
[Linux]:文件(下)
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:Linux学习 贝蒂的主页:Betty’s blog 1. 重定向原理
在明确了文件描述符的概念及其分配规则后,我们就可…
IP网络广播服务平台任意文件上传漏洞
文章目录 免责声明搜索语法漏洞描述漏洞复现修复建议 免责声明
本文章仅供学习与交流,请勿用于非法用途,均由使用者本人负责,文章作者不为此承担任何责任
搜索语法
icon_hash"-568806419"漏洞描述
该系统在upload接口处可上传任…
C++设计模式——State状态模式
一,状态模式的定义
状态模式是一种行为型设计模式,状态模式允许对象在内部状态发生切换时改变它自身的行为。
状态模式的主要目的是将复杂的状态切换逻辑抽象化为一组离散的状态类,使代码结构更加清晰和易于维护。
状态模式将对象的行为封…
一码空传临时网盘PHP源码,支持提取码功能
源码介绍
一码空传临时网盘源码V2.0免费授权,该源码提供了一个简单易用的无数据库版临时网盘解决方案。前端采用了layui开发框架,后端使用原生PHP编写,没有引入任何开发框架,保持了代码的简洁和高效。
这个程序使用了一个无数据…
在树莓派上构建和部署 Node.js 项目
探索在Raspberry Pi上构建和部署Node.js项目的最佳实践。通过我们的专业提示和技巧,克服常见挑战,使您的项目顺利运行。
去年圣诞节,我收到了一份极其令人着迷的礼物,它占据了我许多周末的时间,甚至让我夜不能寐。它就…
FFmpeg 7.0 版本 “Dijkstra”的特点概述
FFmpeg 7.0 FFmpeg 官网:https://ffmpeg.org/FFmpeg 官网更新日志,2024.4.5 号发布代号"Dijkstra"的 7.0 版本的 FFmpeg,如下截图: 为什么叫 Dijkstra“Dijkstra” 指的是艾兹格戴克斯特拉(Edsger Wybe Dijkstra),他是一位荷兰计算机科学家,对计算机科学领域…
TOP 100 AI应用,字节跳动独占6个!
大家好,我是木易,一个持续关注AI领域的互联网技术产品经理,国内Top2本科,美国Top10 CS研究生,MBA。我坚信AI是普通人变强的“外挂”,专注于分享AI全维度知识,包括但不限于AI科普,AI工…
Azure OpenAI models being unable to correctly identify model
题意:Azure OpenAI模型无法正确识别模型。 问题背景:
In Azure OpenAI Studio, while I am able to deploy a GPT-4 instance, the responses are based solely on GPT-3.5 Turbo. I test the same prompts in my personal ChatGPT sub and it returns …
Python OpenCV精讲系列 - 高级图像处理技术(三)
💖💖⚡️⚡️专栏:Python OpenCV精讲⚡️⚡️💖💖 本专栏聚焦于Python结合OpenCV库进行计算机视觉开发的专业教程。通过系统化的课程设计,从基础概念入手,逐步深入到图像处理、特征检测、物体识…
zookeeper是啥?在kafka中有什么作用
一、Zookeeper是啥
问AI,它是这么说: ZooKeeper是一个开源的分布式协调服务。 ZooKeeper最初由雅虎研究院开发,用于解决大型分布式系统中的协调问题,特别是为了避免分布式单点故障。它被设计成一个简单易用的接口集,封…
前端使用 Konva 实现可视化设计器(22)- 绘制图形(矩形、直线、折线)
本章分享一下如何使用 Konva 绘制基础图形:矩形、直线、折线,希望大家继续关注和支持哈! 请大家动动小手,给我一个免费的 Star 吧~ 大家如果发现了 Bug,欢迎来提 Issue 哟~ github源码 gitee源码 示例地址 矩形
先上效…
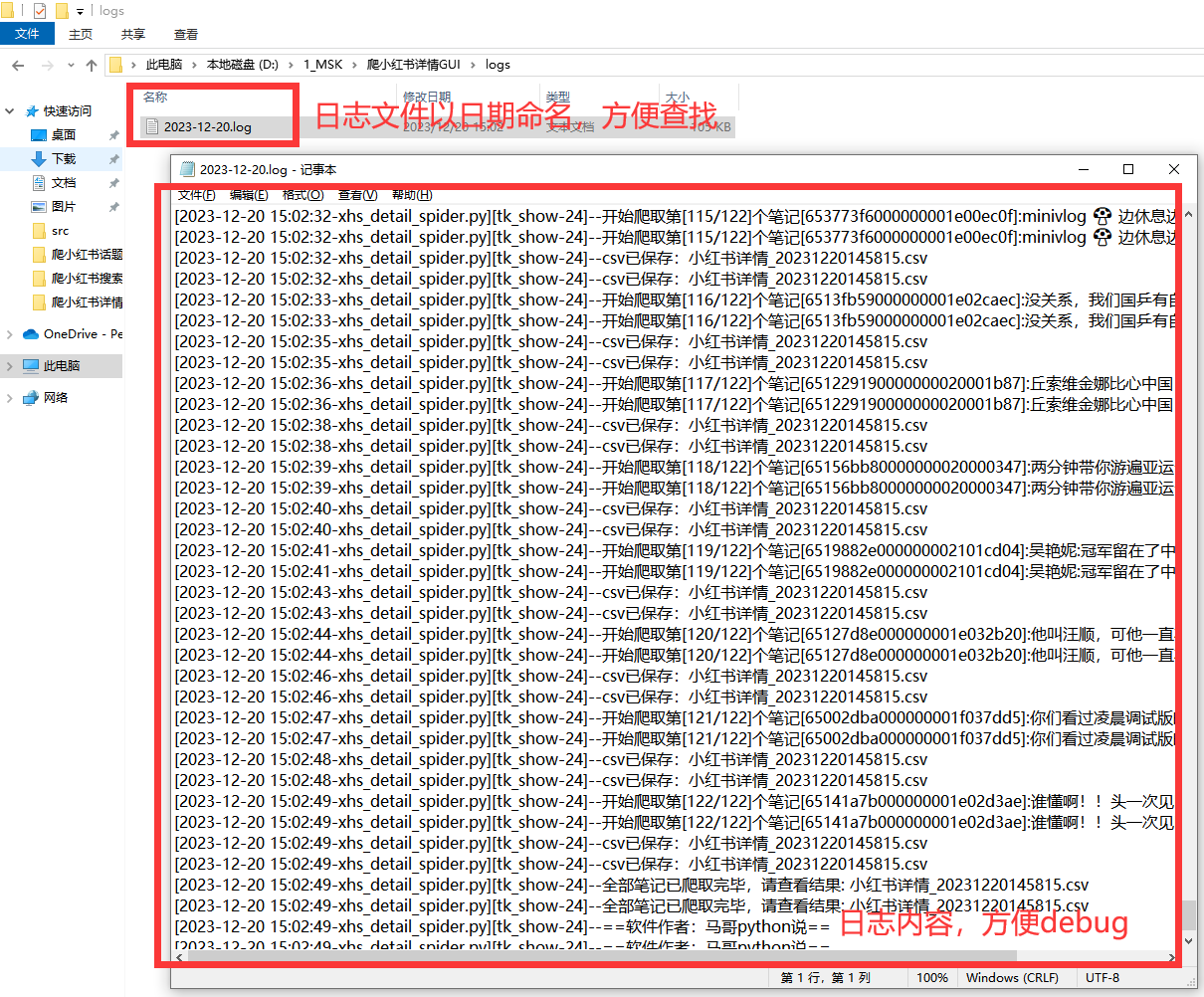
【爬虫软件】小红书笔记批量采集工具,含正文内容、IP属地、转评赞藏等
一、背景介绍
1.1 爬取目标 众所周知,小红书是国内最火热的种草社交平台,拥有海量的高品质用户,尤其以女性用户居多,相对于其他平台更具有消费能力。平台上的爆火笔记也成为众多媒体从业者的分析对象。于是,我用pytho…




![[Linux]:文件(下)](https://img-blog.csdnimg.cn/img_convert/15b9838da8def121b3a555d0a1206039.jpeg)