本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/443781.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
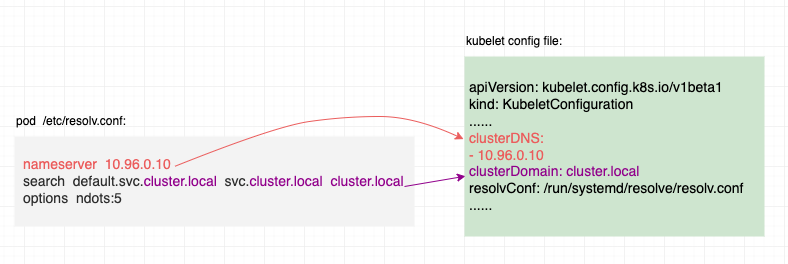
Kubernetes 集群内 DNS
DNS 简介
在互联网早期,随着连接设备数量的增加,IP 地址的管理与记忆变得越来越复杂。为了简化网络资源的访问,DNS(Domain Name System)应运而生。DNS 的核心作用是将用户可读的域名(如 www.example.com&a…
C++伟大发明--模版
C起初是不受外界关注的,别人觉得他和C语言没有本质上的区别,只是方便些,直到祖师爷发明了模版,开始和C语言有了根本的区别。
我们通过一个小小的例子来搞清楚什么是模版,模版的作用到底有多大,平时我们想要…
Flask-JWT-Extended登录验证
1. 介绍 """安装:pip install Flask-JWT-Extended创建对象 初始化与app绑定jwt JWTManager(app) # 初始化JWTManager设置 Cookie 的选项:除了设置 cookie 的名称和值之外,你还可以指定其他的选项,例如:过期时间 (max_age)&…
【楚怡杯】职业院校技能大赛 “云计算应用” 赛项样题四
某企业根据自身业务需求,实施数字化转型,规划和建设数字化平台,平台聚焦“DevOps开发运维一体化”和“数据驱动产品开发”,拟采用开源OpenStack搭建企业内部私有云平台,开源Kubernetes搭建云原生服务平台,选…
简单题21 - 合并两个有序链表(Java)20240917
问题描述: java代码:
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val val; }* ListNode(int val, ListNode next) { this.val val…
C语言 ——— 编写函数,判断一个整数是否是回文整数
目录
题目要求
代码实现 题目要求
编写一个函数,用来判断一个整数是否是回文整数,如果是回文整数就返回 true ,如果不是就返回 false
举例说明: 输入:121 输出:true 输入:1321 输出…
VBS学习1 - 语法、内置函数、内置对象
文章目录 概述执行脚本语法转义字符文本弹框msgbx定义变量dim(普通类型)定义接收对象set字符拼接&用户自定义输入框inputbox以及输入判断ifelse数组(参数表最大索引,非数组容量)有容量无元素基于元素确定容量 循环…
828华为云征文|部署在线文件管理器 Spacedrive
828华为云征文|部署在线文件管理器 Spacedrive 一、Flexus云服务器X实例介绍1.1 云服务器介绍1.2 产品优势1.3 计费模式 二、Flexus云服务器X实例配置2.1 重置密码2.2 服务器连接2.3 安全组配置 三、部署 Spacedrive3.1 Spacedrive 介绍3.2 Docker 环境搭建3.3 Spac…
反转字符串 II--力扣541
反转字符串 II 题目思路代码 题目 思路
本题的关键在于理解每隔 2k 个字符的前 k 个字符进行反转,剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符。并且剩余字符少于 k 个,则将剩余字符全部反转。
让i每次跳2k,成为每一次…
考软考的信息安全工程师,有什么诀窍在一个月内通过吗?
一般是至少是2个月时间拿来备考的,低于2个月的话,时间肯定是比较赶的。虽然一个月时间相对紧张,但通过合理规划和高效利用时间,也是有可能成功通过考试的。以下是一份详细的备考策略,旨在帮助大家在有限的时间内最大化…
AI客服机器人开启企业客户服务新纪元
随着人工智能(AI)技术的迅猛发展,使得AI客服机器人走进了我们的视野,成为提高客户满意度和业务效率的不二法宝。这些智能机器人不仅能够处理海量信息,还能为客户提供个性化的服务体验。 一、AI客服机器人的基本原理
AI客服机器人是基于人工智…
TCP并发服务器的实现
一请求一线程
问题
当客户端数量较多时,使用单独线程为每个客户端处理请求可能导致系统资源的消耗过大和性能瓶颈。
资源消耗:
线程创建和管理开销:每个线程都有其创建和销毁的开销,特别是在高并发环境中,这种开销…
MySQL高阶1777-每家商店的产品价格
题目
找出每种产品在各个商店中的价格。
可以以 任何顺序 输出结果。
准备数据
create database csdn;
use csdn;Create table If Not Exists Products (product_id int, store ENUM(store1, store2, store3), price int);
Truncate table Products;
insert into Products …
ZYNQ FPGA自学笔记~点亮LED
一 ZYNQ FPGA简介 ZYNQ FPGA主要特点是包含了完整的ARM处理系统,内部包含了内存控制器和大量的外设,且可独立于可编程逻辑单元,下图中的ARM内核为 ARM Cortex™-A9,ZYNQ FPGA包含两大功能块,处理系统Processing System…
十款主流的供应链管理系统盘点,优缺点一目了然!
本文将盘点十款供应链管理系统,为企业选型提供参考! 想象一下,一家企业在生产和销售产品的过程中,原材料供应不及时、库存积压严重、物流配送混乱。这时,供应链管理系统就如同一位高效的指挥家,将各个环节紧…
Hazel 2024
不喜欢游戏的人也可以做引擎,比如 cherno 引擎的作用主要是有两点: 将数据可视化交互 当然有些引擎的功能也包含有制作数据文件,称之为资产 assets 不做窗口类的应用栈,可能要花一年才能做一个能实际使用的应用,只需…
OpenHarmony(鸿蒙南向开发)——标准系统方案之瑞芯微RK3568移植案例(上)
往期知识点记录: 鸿蒙(HarmonyOS)应用层开发(北向)知识点汇总 鸿蒙(OpenHarmony)南向开发保姆级知识点汇总~ OpenHarmony(鸿蒙南向开发)——轻量和小型系统三方库移植指南…
[C++进阶[六]]list的相关接口模拟实现
1.前言
本章重点 在list模拟实现的过程中,主要是感受list的迭代器的相关实现,这是本节的重点和难点。 2.list接口的大致框架 list是一个双向循环链表,所以在实现list之前,要先构建一个节点类
template <class T>
struct L…

















![[C++进阶[六]]list的相关接口模拟实现](https://i-blog.csdnimg.cn/direct/d82f876baa9c48d180b9982b94952d59.png)