本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/61343.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
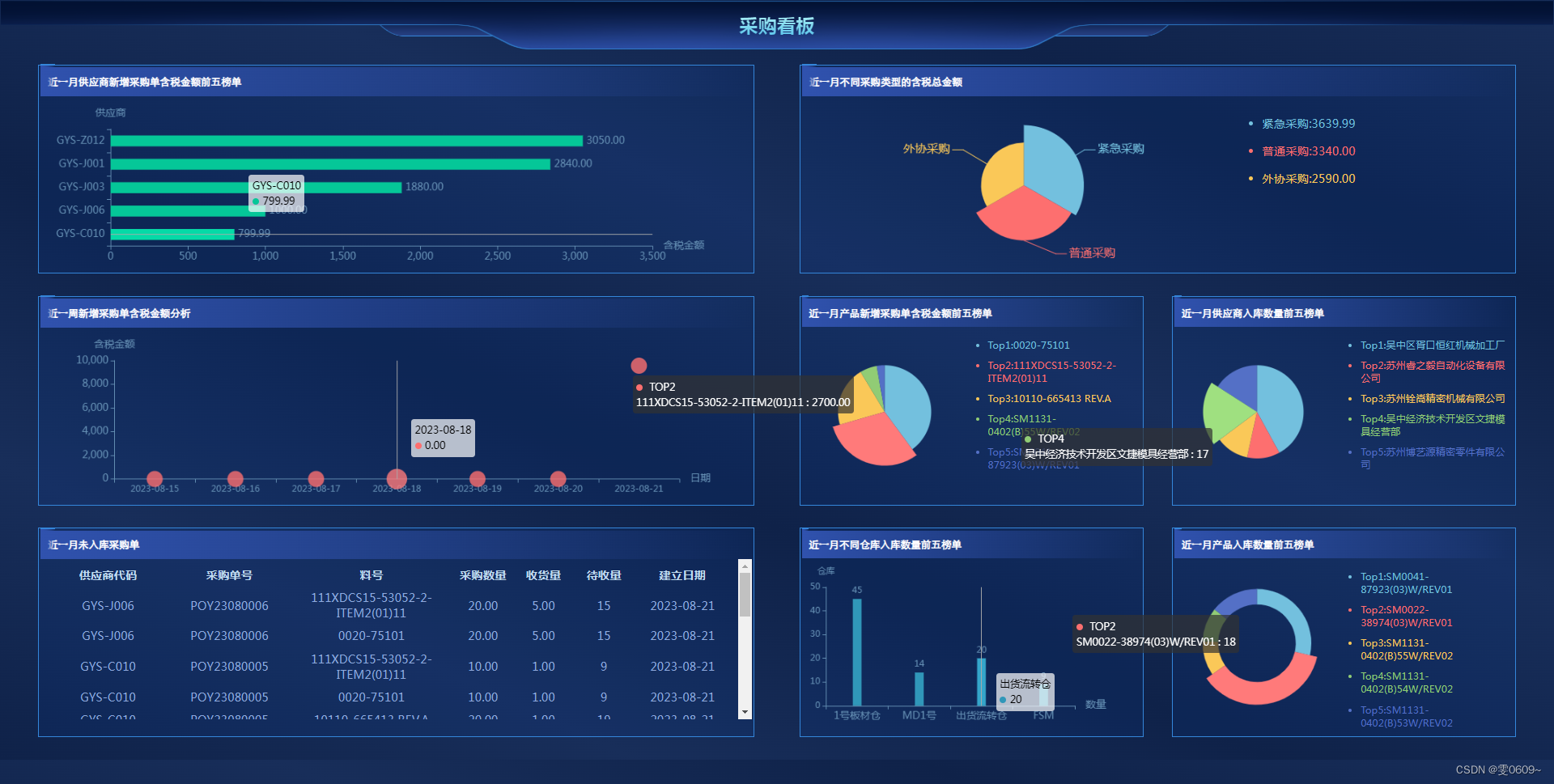
php+echarts实现数据可视化实例3
效果 全部代码
<?php
include(includes/session.inc);
include(includes/SQL_CommonFunctions.inc);
?>
<!DOCTYPE html>
<html lang"en">
<head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" …
报错sql_mode=only_full_group_by
首发博客地址 https://blog.zysicyj.top/ 报错内容 ### The error may exist in file[D:\code\cppCode20221025\leader-system\target\classes\mapper\system\TJsonDataMapper.xml] ### The error may involve defaultParameterMap ### The error occurred while…
【编织时空三:探究顺序表与链表的数据之旅】
本章重点 链表OJ题 1. 删除链表中等于给定值 val 的所有结点。 OJ链接
思路一:删除头结点时另做考虑(由于头结点没有前一个结点) struct ListNode* removeElements(struct ListNode* head, int val) {assert(head);struct ListNode* cur h…
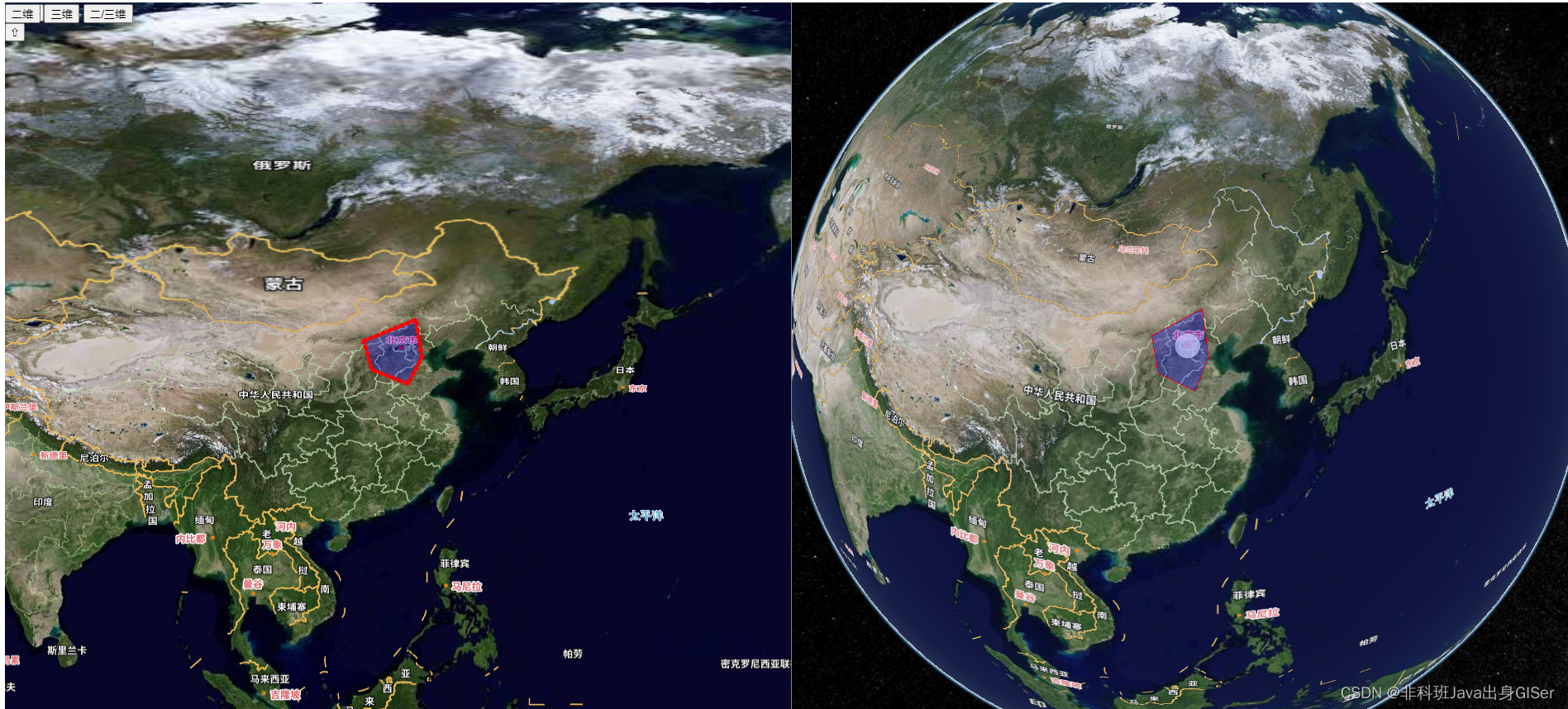
ol-cesium 暴露 Cesium viewer 对象以及二三维切换、viewer 添加点功能示例
ol-cesium 暴露 Cesium viewer 对象以及二三维切换、viewer 添加点功能示例 核心代码完整代码在线示例 二三维一体化的概念一直都比较火热,虽然大多数都是狭义的概念,但是很多需求方也想要这样的功能。
Openlayers 官方出了一个二三维一体化的工具&…
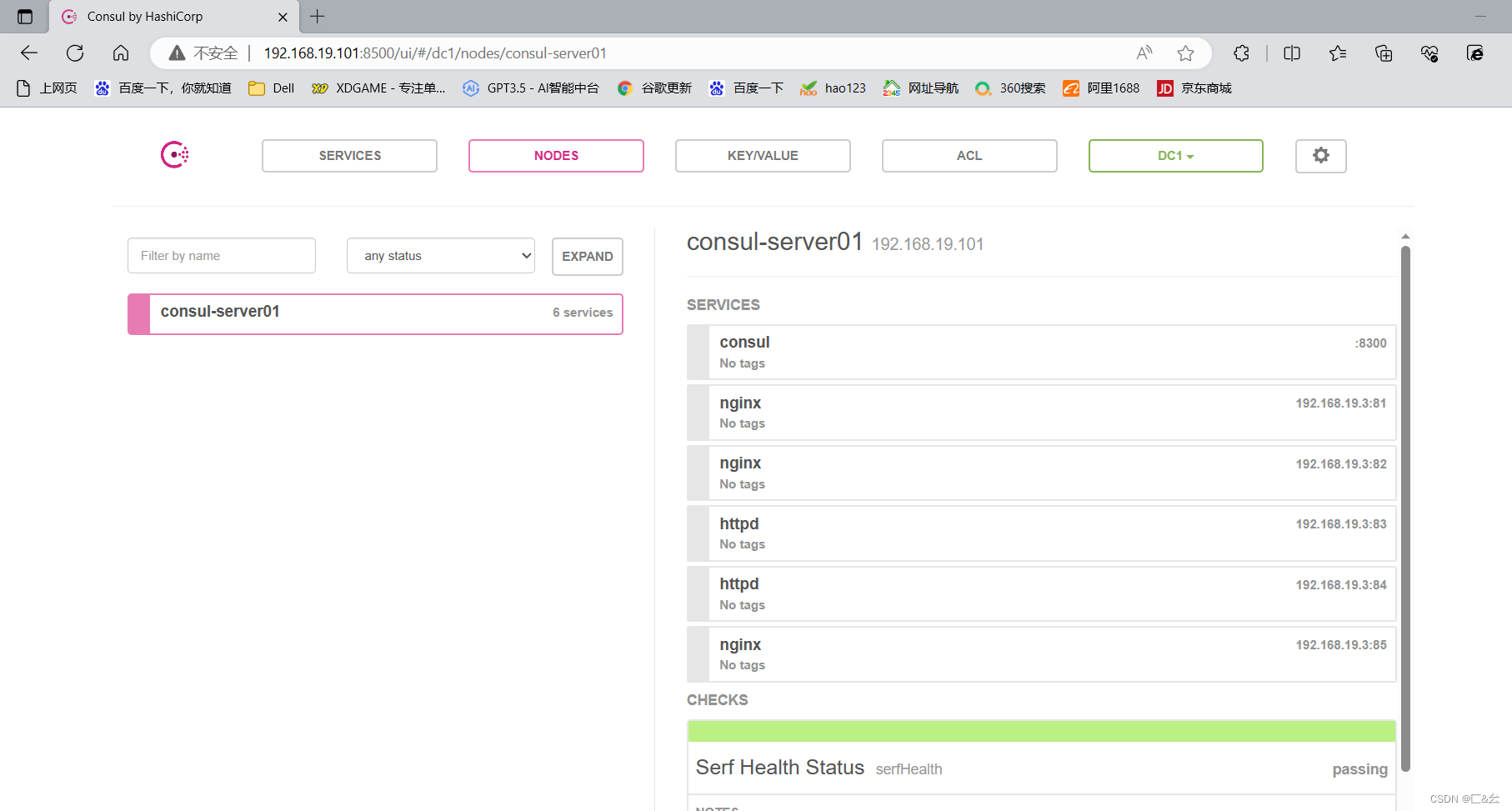
docker之Consul环境的部署
目录 一、Docker consul的介绍
1.1 template模板(更新)
1.2 registrator(自动发现)
1.3 agent(代理)
二.consul的工作原理
三.Consul的特性
四.Consul的使用场景
五.搭建Consul的集群
5.1 需求
5.2 部署consul
5.3 主服务器部署[192.168.19.10…
【工具使用】Git的使用
dev代表开发版 1. git clone 命令
通过 git add <name> 对文件进行跟踪,把<name>加入到暂存区
git commit -m XXXXXXX 提交修改并补充XXXXX作为注释
“暂存”状态:出现了一些修改,但是还没有提交 对于Java来说,.cl…
SpringBoot接收参数的8种方式
文章目录 1. 直接把请求参数写在方法的形参中2. 封装一个bean直接来接收3. 原生的HttpServletRequest接收4. PathVariable获取rest风格路径参数5. RequestParam绑定请求参数到方法形参6. RequestBody绑定请求参数到方法形参7. RequestHeader8. CookieValue 1. 直接把请求参数写…
春秋云镜:CVE-2018-19422(Subrion CMS 4.2.1 存在文件上传漏洞)
一、题目 靶标介绍:
Subrion CMS 4.2.1 存在文件上传漏洞
进入题目:
admin/admin 点击设置: 后台管理主页: 上传页面: 上传目录:
/panel/uploads/ 查看上传位置:
system.pht<?php sys…
kafka-python 消费者消费不到消息
排除步骤1:
使用group_id”consumer_group_id_001“ 和 auto_offset_reset"earliest"
from kafka import KafkaConsumerconsumer KafkaConsumer(bootstrap_servers["dev-kafka01.test.xxx.cloud:9092"],enable_auto_commitTrue, auto_commit…
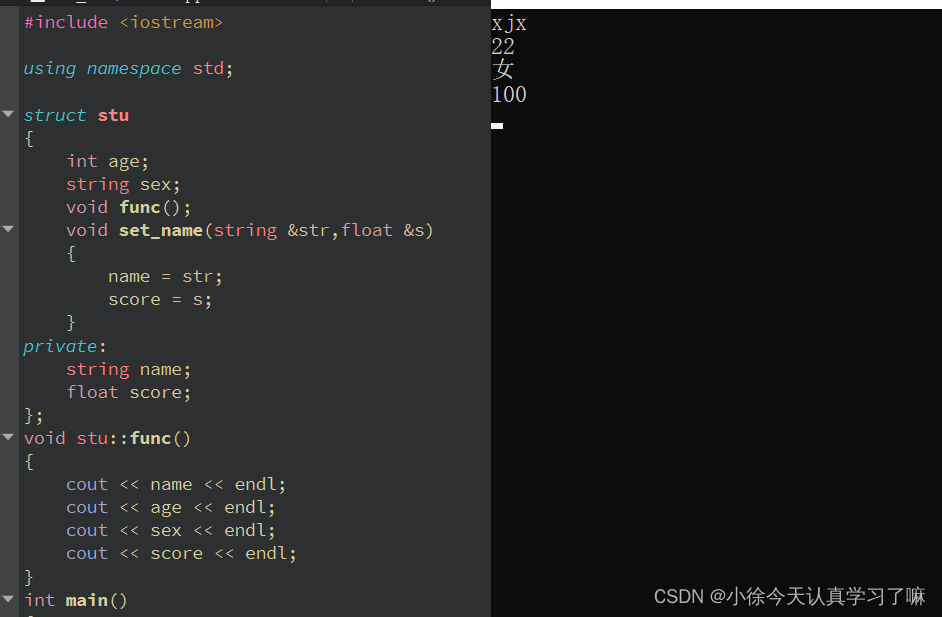
C++day2作业(2023.8.22)
1.定义一个学生的结构体,包含学生的姓名,年龄,成绩,性别,学生的成绩,姓名,定义为私有权限;定义一个学生类型的结构体变量,设置公有函数用于给学生的成绩和名字进行赋值&a…
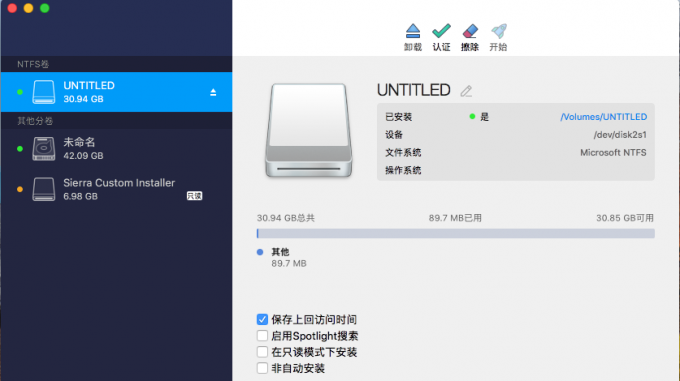
苹果电脑读取u盘第三方工具Paragon NTFS15
Paragon NTFS for Mac 15 简体中文标准版轻量级的快捷菜单,可执行挂载、卸载和验证操作。软件设计优秀,与 macOS 无缝衔接,操作简单。 功能特点
一、所有操作只需轻轻一点 轻量级的快捷菜单栏,可访问所有NTFS驱动器并执行最常见的…
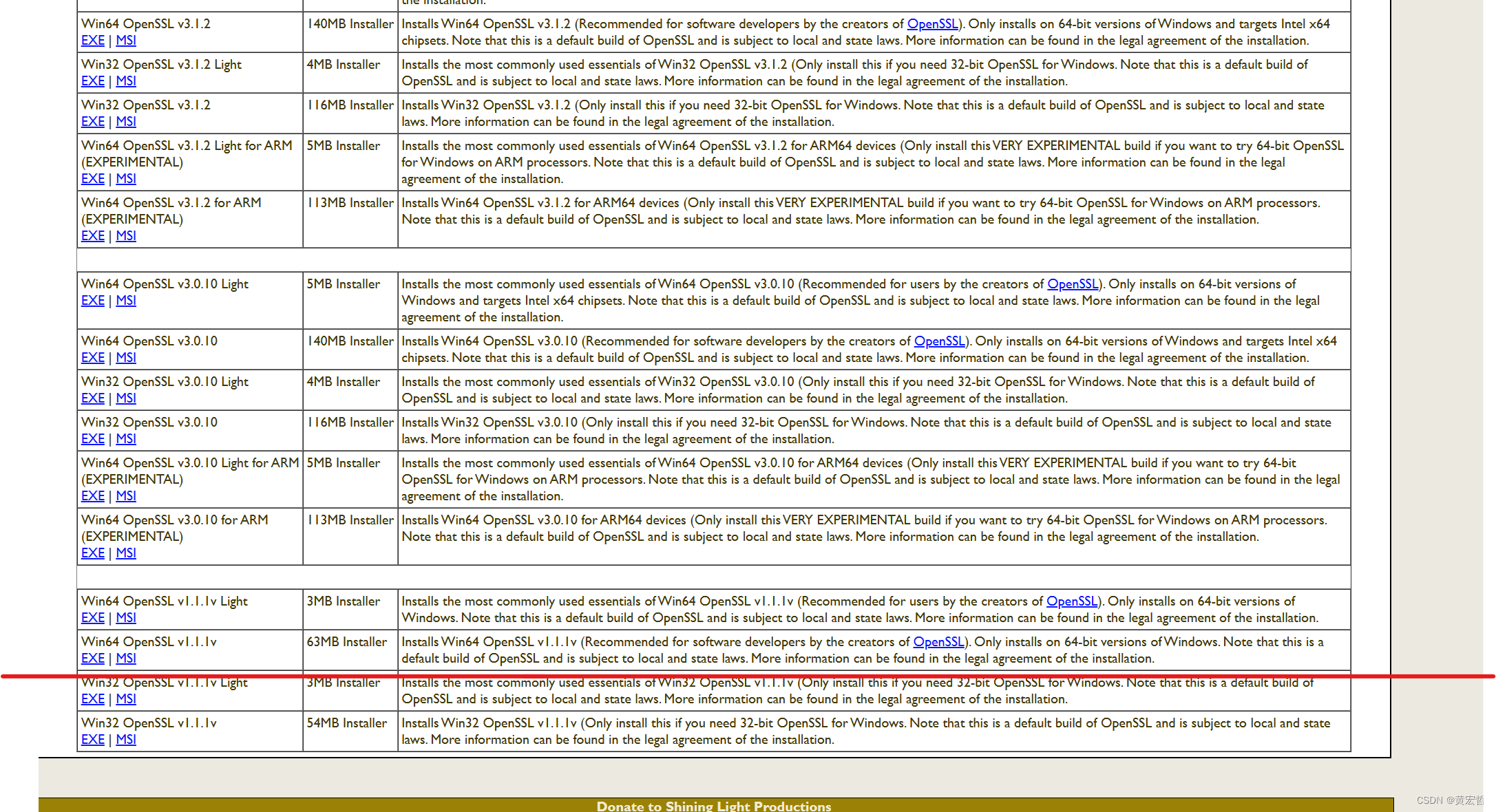
qt5 TLS initialization failed error
首先打印openssl支持信息
qDebug() << QSslSocket::supportsSsl() << "\n";
qDebug() << QSslSocket::sslLibraryBuildVersionString();
//上述代码打印下面的结果:
false
"OpenSSL 1.1.1g 21 Apr 2020"更新对应openssl证…
变频器和plc之间无线MODBUS通讯
在工业现场由PLC远程控制变频器的应用非常常见,如果挖沟布线不便或者变频器在移动设备上,那么采用无线通讯就是最佳方案。
这里我们选用最常用的三菱 FX2N PLC和三菱变频器为例,并结合日系plc专用无线通讯终端DTD435M来说明PLC与变频器之间的…
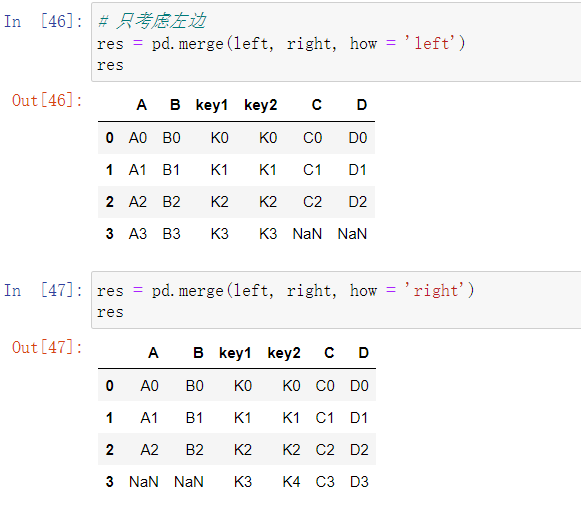
Pandas学习笔记
Pandas数据分析处理库
数据预处理
导入一份泰坦尼克号乘客数据 df.head()展示读取数据,默认读取前5行
df.tail()默认读取后5行
df.head(10)读取前10行DataFrame结构
Pandas工具包的基础结构,二维矩阵结构,行表示数据样本,列表示…
支付宝订单金额原路退回
以PHP为例:
参考支付宝官方文档地址:
小程序文档 - 支付宝文档中心支付宝文档中心https://opendocs.alipay.com/open/6c0cdd7d_alipay.trade.refund操作步骤:
一:下载SDK
二:沙箱测试 登录支付宝账号后,…
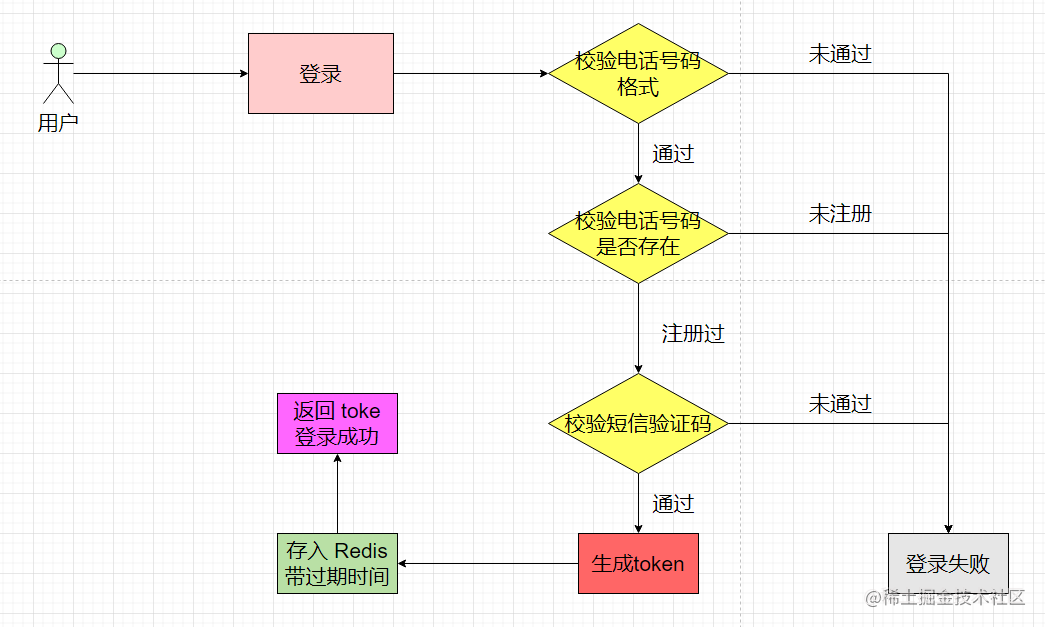
个人就能搞定的短信登录,实用!
个人项目:社交支付项目(小老板) 作者:三哥,https://j3code.cn 项目文档:https://www.yuque.com/g/j3code/dvnbr5/collaborator/join?tokenCFMcFNwMdhpp6u2s&sourcebook_collaborator# 预览地址(未开发…
solidity0.8.0的应用案例12:通用可升级合约UUPS
代理合约中选择器冲突(Selector Clash)的另一个解决办法:通用可升级代理(UUPS,universal upgradeable proxy standard)。代码由OpenZeppelin的UUPSUpgradeable简化而成,不应用于生产。
UUPS
作为透明代理的替代方案,UUPS也能解决"选择器冲突"(Selector Cl…
取模运算符在数组下标的应用
什么是取模运算符%? 定义: a mod b,设a、b属于正整数且b>0,如果q、r属于正整数满足aq*br,且0≤r<b,则定义: a mod b r 注意:取模运算符两侧的除数和被除数都是整数ÿ…