本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/75286.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
8.26day46(多重背包 背包结束)
多重背包问题
相比于01背包:01背包数量是为1 多重背包中数量大于1
解决方法:转换成01背包 139. 单词拆分 - 力扣(LeetCode)
爬虫(bilibili热门课程记录)
什么是爬虫?程序蜘蛛,沿着互联网获取相关信息,收集目标信息。
一、python环境安装
1、先从Download Python | Python.org中下载最新版本的python解释器
2、再从Download PyCharm: Python IDE for Professional Developers by JetBrains中下…
大数据(三)大数据相关的职位
大数据(三)大数据相关的职位 本文目录:
一、写在前面的题外话
二、2022年就业状况
2.1、不同企业性质高校毕业生 CIER 指数
2.2、不同企业规模高校毕业生 CIER 指数
2.3、高校毕业生供求 TOP15 城市
2.4、一季度景气指数较高和较低的行…
路径规划 | 图解Theta*算法(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 A*算法的局限性2 Theta*算法原理图解3 Bresenham视线法4 算法仿真测试4.1 算法流程图4.2 ROS C 实现4.3 Python实现4.4 Matlab实现 0 专栏介绍
🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全…
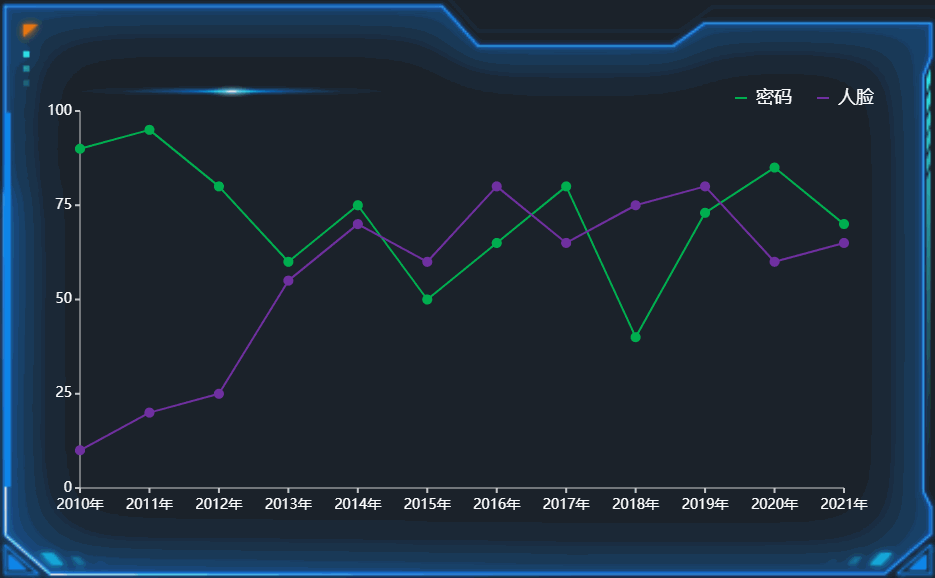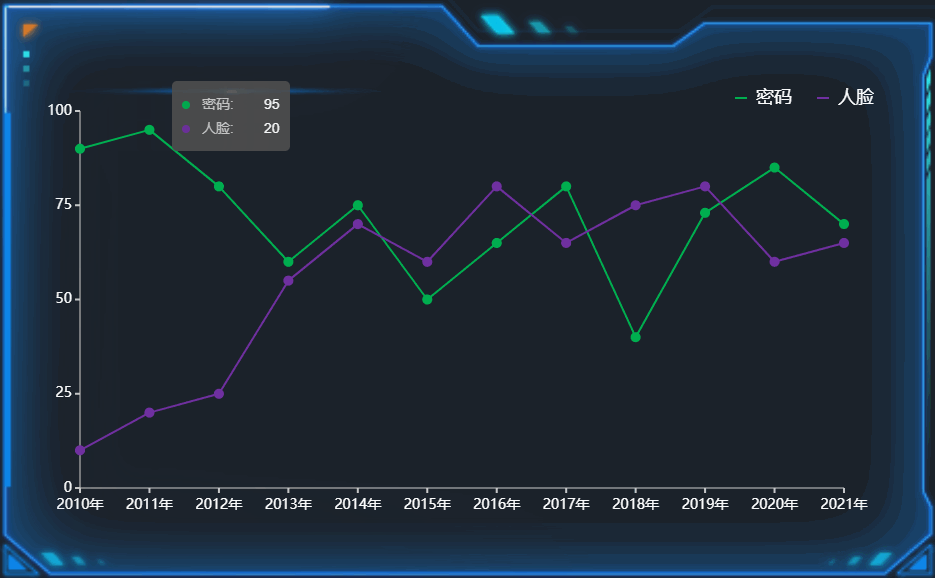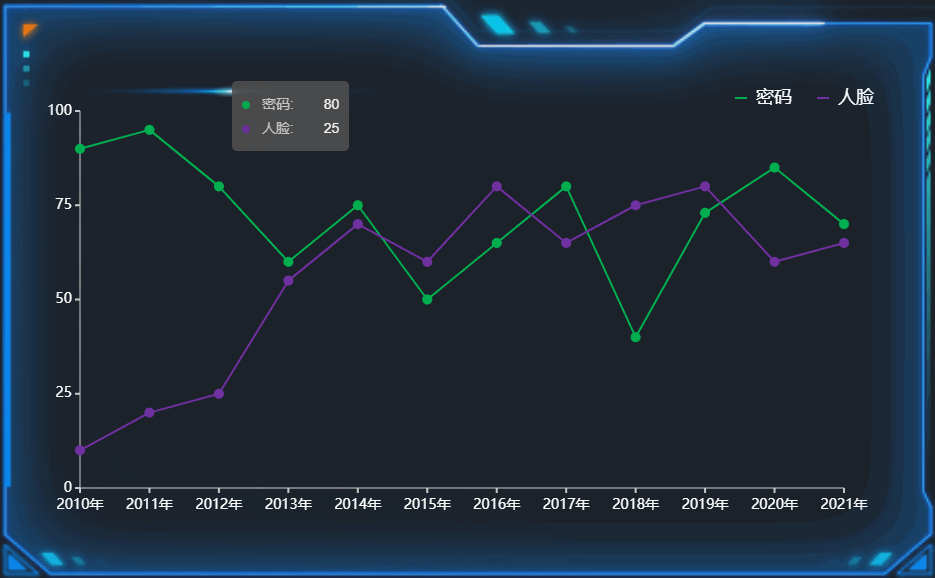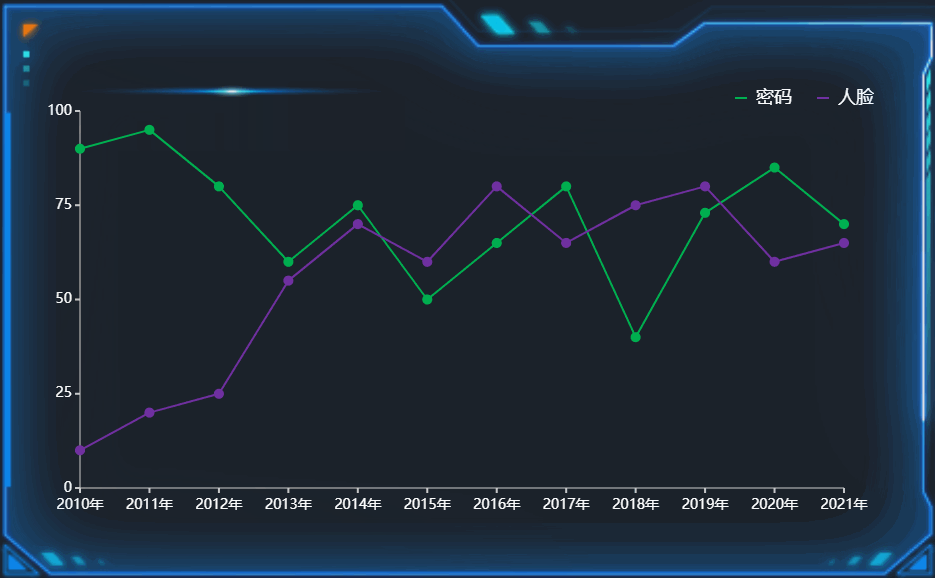
数据之美:探索数据可视化设计的奇妙世界
在信息时代的浪潮中,海量的数据正在影响着我们的生活和决策。然而,数据本身虽然有力量,但如何将其有机地呈现给我们,却成为了一个挑战。数据可视化设计应运而生,它不仅让枯燥的数字变得生动,还带来了一场视…
DBi Tech Studio Controls for .NET Crack
DBi Tech Studio Controls for .NET Crack Studio Controls for.NET为企业开发人员提供了一套全面的Windows布局和信息表示软件元素,面向搜索业务分析商业调度和UI表示控制器的程序员。Studio Controls for.NET包含17个免版税的.NET Windows窗体控件,用于…
cyclictest stress 工具 使用
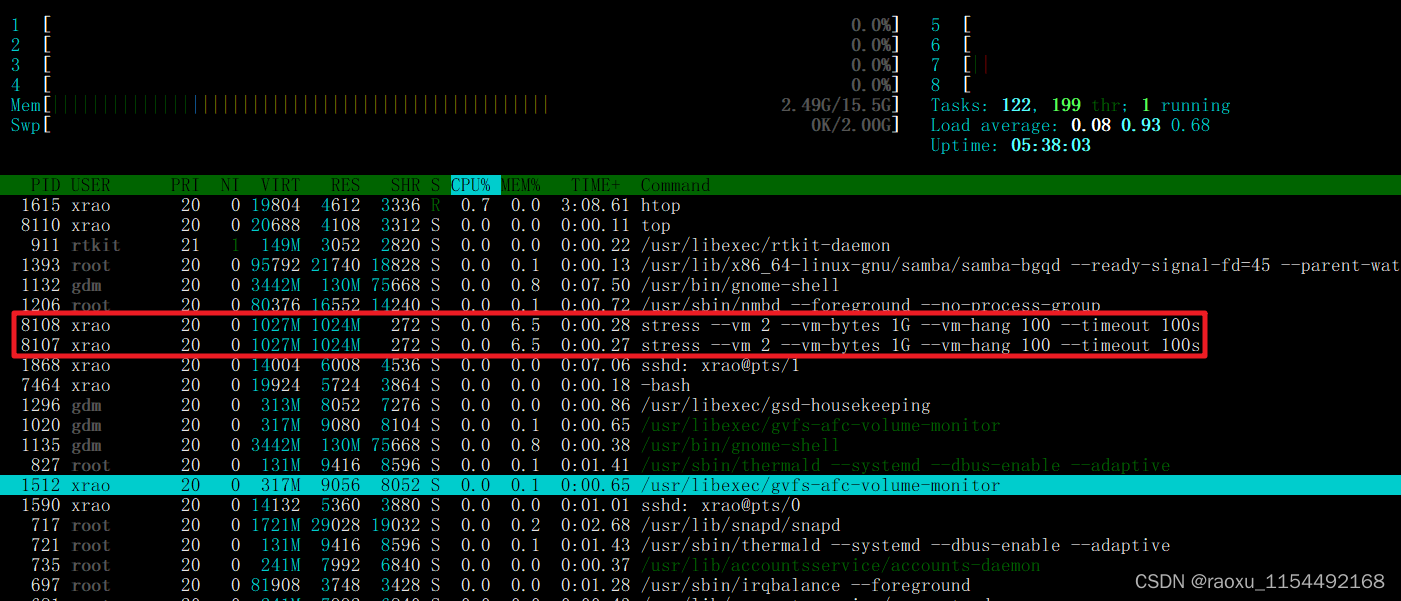
工具介绍
1. Cyclictest 准确且重复地测量线程的预期唤醒时间与它实际唤醒的时间之间的差异,以提供有关系统延迟的统计数据。 它可以测量由硬件、固件和操作系统引起的实时系统延迟 2.stress是Linux的一个压力测试工具,可以对CPU、Memory、IO、磁盘进行…
助力养殖行业数字化转型,基于深度学习模型开发构建牛脸识别系统
在我们以往接触到的项目或者是业务场景中,大多牵涉到生物特征识别的任务基本都是人脸识别,这也是目前我们每天都会接触到的应用,比如:上下班的打卡、支付时的刷脸等等,这也是比较成熟的一项AI应用。
这里我们简单对一…
Java【手撕双指针】LeetCode 15. “三数之和“, 图文详解思路分析 + 代码
文章目录 前言一、三数之和1, 题目2, 思路分析3, 代码 前言 各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你: 📕 JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等 📗 Java数据结构: 顺序表, 链表, 堆…
【Java 中级】一文精通 Spring MVC - 转发重定向(四)
👉博主介绍: 博主从事应用安全和大数据领域,有8年研发经验,5年面试官经验,Java技术专家,WEB架构师,阿里云专家博主,华为云云享专家,51CTO 专家博主 ⛪️ 个人社区&#x…
求解整数规划问题的割平面法和分支定界法
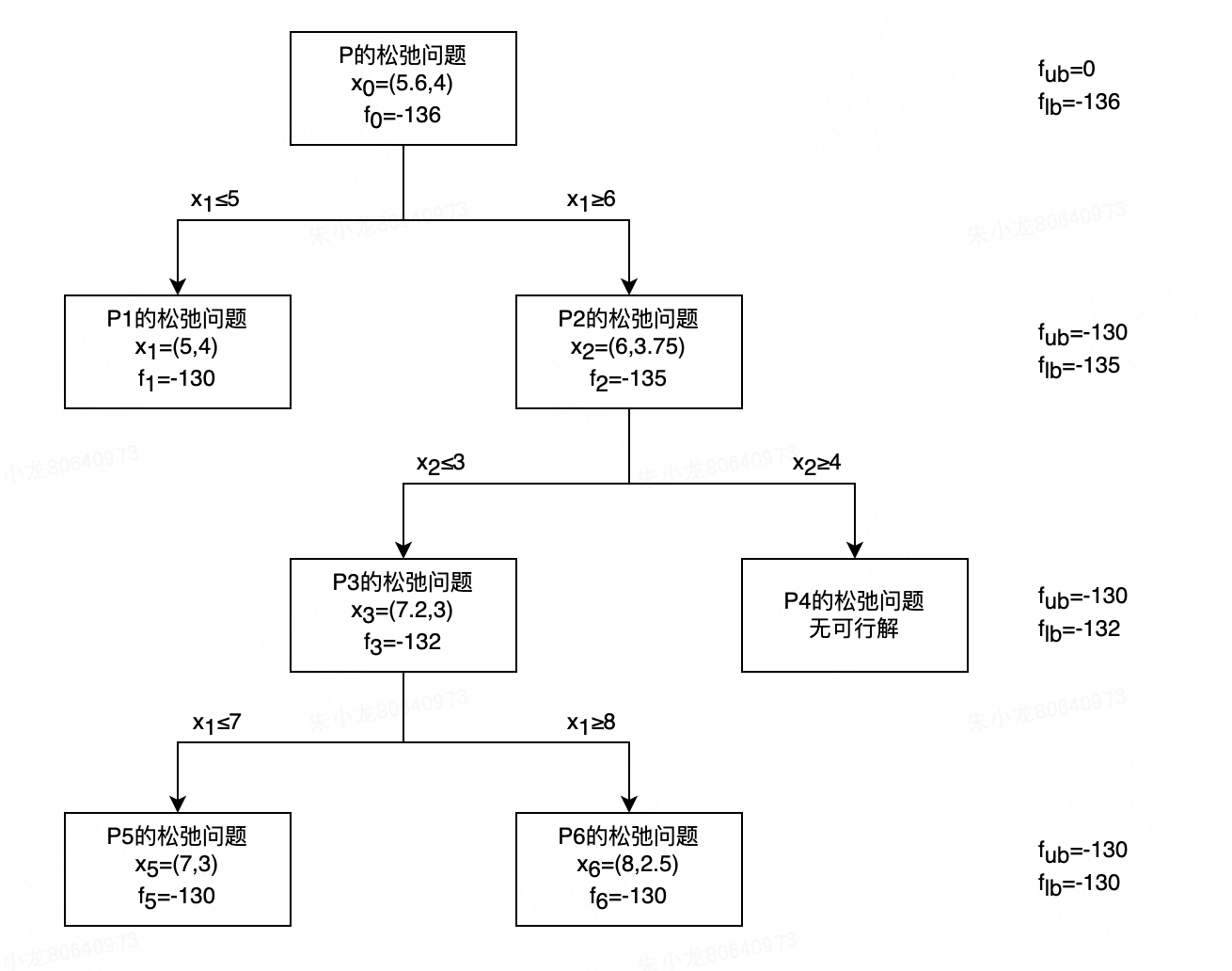
文章目录 整数规划割平面法分支定界法代码实现 整数规划
整数规划问题是优化变量必须取整数值的线性或非线性规划问题,不过,在大多数情况下,整数规划问题指的是整数线性规划问题。
其数学模型为 m i n f ( x ) c T x s.t A x b x ≥ 0 x…
《网络是怎样连接的》(五)
本文主要取材于 《网络是怎样连接的》 第五章。
目录
5.1 Web服务器的部署地点 5.2 防火墙的结构和原理
5.3服务器负载平衡
5.4 使用缓存服务器分担负载
5.5 内容分发服务 简述:本文主要内容是解释 网络包如何朝服务器前进,并通过服务器前面的防…
Excel·VBA二维数组组合函数、组合求和
目录 1,二维数组组合函数举例 2,组合求和 之前的文章《ExcelVBA数组组合函数、组合求和》和《ExcelVBA数组排列函数》,都是针对一维数组的组合和排列 二维数组组合:对一个m行*n列的二维数组,每行抽取1个元素进行组合&a…
JavaScript基础语法
一、JavaScript编写方式
位置一:HTML代码行内(不推荐)
<!-- 方式一:行内编写 -->
<a href"javascript:alert(hello world)">hello world</a>
<!-- 方式二:行内编写,通过监…
正中优配:多只内房股沦为仙股 投资者信心何时恢复?
8月25日,受房地产利好方针推进,房地产板块直线大幅拉升,其中在港交所上市的富力地产大涨超过5%,股价重回1港元/股上方,然后暂时摆脱了“仙股”的称号。 实践上,近期,碧桂园、融创我国、SOHO我国…
vue2 路由进阶,VueCli 自定义创建项目
一、声明式导航-导航链接
1.需求
实现导航高亮效果 如果使用a标签进行跳转的话,需要给当前跳转的导航加样式,同时要移除上一个a标签的样式,太麻烦!!!
2.解决方案
vue-router 提供了一个全局组件 router…
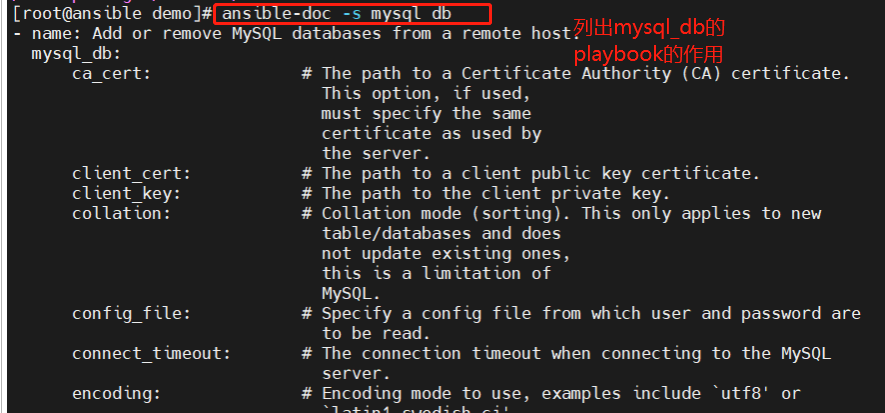
自动化运维工具-----Ansible入门详解
目录
一.Ansible简介
什么是Ansible? Ansible的特点 Ansible的架构 二.Ansible任务执行解析
ansible任务执行模式 ansible执行流程
ansible命令执行过程 三.Ansible配置解析
ansible的安装方式
ansible的程序结构(yum安装为例) ansibl…
什么是异步编程?什么是回调地狱(callback hell)以及如何避免它?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 异步编程⭐ 回调地狱(Callback Hell)⭐ 如何避免回调地狱1. 使用Promise2. 使用async/await3. 模块化和分离 ⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订…