本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/833.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Rabbitmq的安装与使用(Linux版)
目录
Rabbitmq安装
1.在Ubuntu上安装RabbitMQ:
打开终端,运行以下命令以更新软件包列表:
安装RabbitMQ:
安装完成后,RabbitMQ服务会自动启动。你可以使用以下命令来检查RabbitMQ服务状态:
2.在CentOS…
DHorse v1.3.0 发布,基于k8s的发布平台
综述
DHorse是一个简单易用、以应用为中心的云原生DevOps系统,具有持续集成、持续部署、微服务治理等功能,无需安装依赖Docker、Maven、Node等环境即可发布Java、Vue、React应用,主要特点:部署简单、操作简洁、功能快速。
新增特…
1.2 网络安全法律法规
数据参考:CISP官方
目录
国家立法体系网络安全法解析网络安全相关法律
一、国家立法体系
1、我国的立法体系
我国的立法体系在网络空间治理中扮演着基础工作的角色。为了应对快速发展的网络技术和威胁,我国采取了多级立法机制来完善网络空间的法律…
第17节 R语言分析:生物统计数据集 R 编码分析和绘图
生物统计数据集 R 编码分析和绘图
生物统计学,用于对给定文件 data.csv 中的医疗数据应用 R 编码,该文件是患者人口统计数据集,包含有关来自各种祖先谱系的个体的标准信息。
数据集特征解释 脚本
output= file("Output.txt") # File name of output log
sink(o…
LeetCode[面试题04.08]首个共同祖先
难度:Medium
题目: 设计并实现一个算法,找出二叉树中某两个节点的第一个共同祖先。不得将其他的节点存储在另外的数据结构中。注意:这不一定是二叉搜索树。 例如,给定如下二叉树: root [3,5,1,6,2,0,8,null,null,7,…
vue项目中对组件使用v-model绑定值,在vue3中如何更新数据
在el-form 中 el-form-item 绑定组件进行校验 想在表单下面爆红提示 可以对组件使用v-model绑定值 vue2 通过this.$emit(‘input’,value) 更新 v-model值 vue3 通过this.$emit(‘update:modelValue’ ,value) 更新 v-model值
Neo4j 集群和负载均衡
Neo4j 集群和负载均衡
Neo4j是当前最流行的开源图DB。刚好读到了Neo4j的集群和负载均衡策略,记录一下。
1 集群
Neo4j 集群使用主从复制实现高可用性和水平读扩展。
1.1 复制
集群的写入都通过主节点协调完成的,数据先写入主机,再同步到…
UNIX网络编程卷一 学习笔记 第二十六章 线程
在传统UNIX模式中,当一个进程需要另一个实体完成某事时,它就fork一个子进程,并让子进程去执行处理,Unix上大多网络服务器程序就是这么写的。
这种范式多年来一直用得很好,但fork调用存在一些问题: 1.fork调…
【C语言初阶(20)】调试练习题
文章目录 前言实例1实例2 前言
在我们开始调试之前,应该有个明确的思路;程序是如何完成工作的、变量到达某个步骤时的值应该是什么、出现的问题大概会在什么位置。这些东西在调试之前都需要先确认下来,不然自己都不知道自己在调试个什么东西…
【Python系列】Python基础语法轻松入门—从变量到循环
目录
写在前面
语法介绍
变量
数据类型
整数
浮点数
字符串
列表
元组
字典
运算符
算术运算符
比较运算符
逻辑运算符
条件语句
循环语句
图书推荐
图书介绍
参与方式
中奖名单 写在前面 Python 是一种高级、解释型的编程语言,具有简单易学…
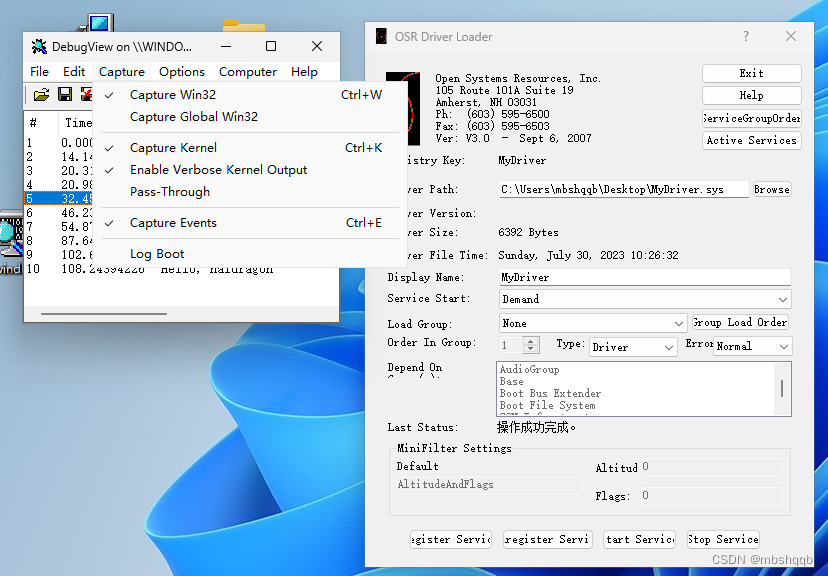
Windows驱动开发
开发Windows驱动程序时,debug比较困难,并且程序容易导致系统崩溃,这时可以使用Virtual Box进行程序调试,用WinDbg在主机上进行调试。
需要使用的工具:
Virtual Box:用于安装虚拟机系统,用于运…
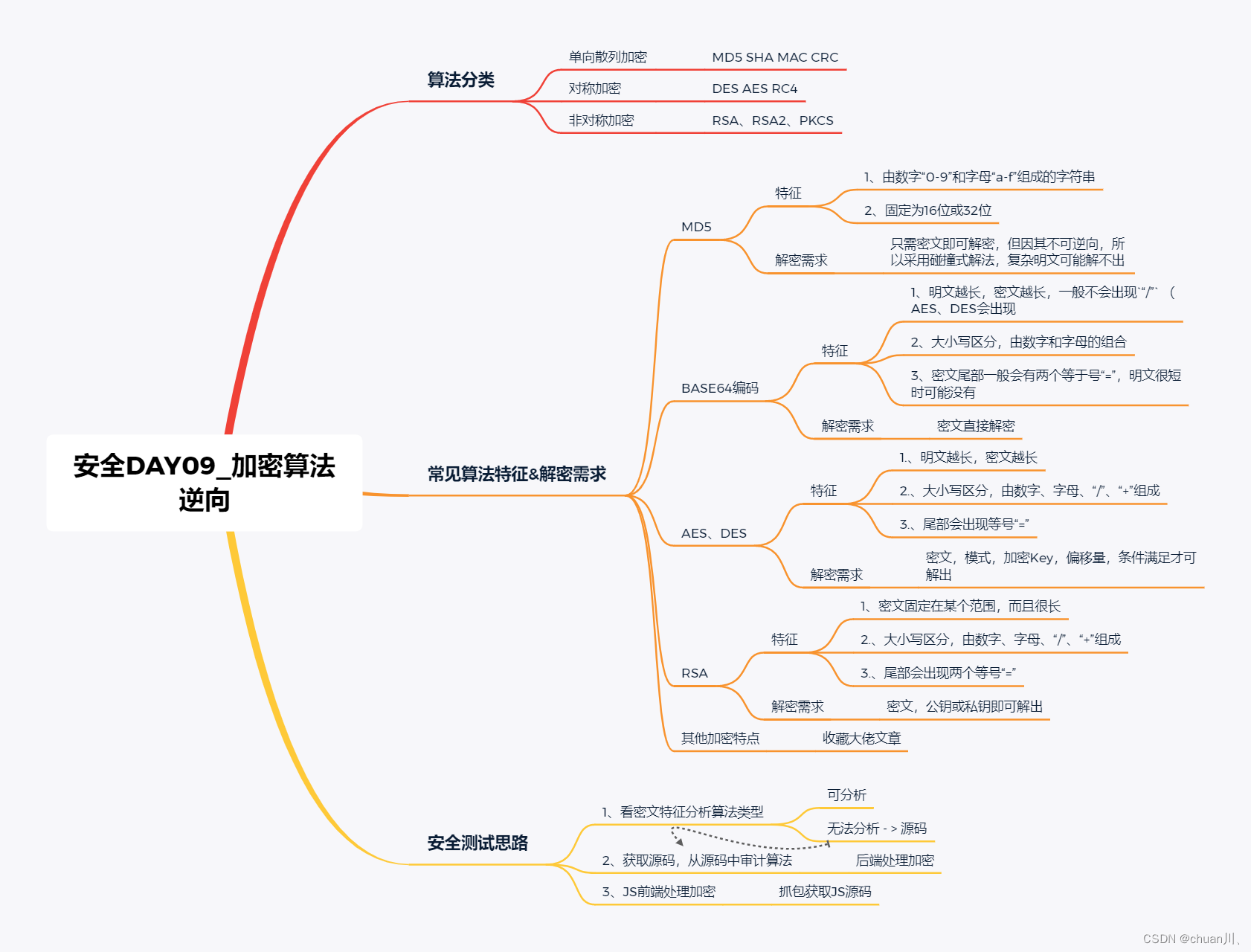
安全学习DAY09_加密逆向,特征识别
算法逆向&加密算法分类,特征识别 文章目录 算法逆向&加密算法分类,特征识别算法概念,分类单向散列加密 - MD5对称加密 - AES非对称加密 - RSA 常见加密算法识别特征,解密特点MD5密文特点BASE64编码特点AES、DES特点RSA密文…
C++STL序列式容器——list容器及其常用操作(详解)
纵有疾风起,人生不言弃。本文篇幅较长,如有错误请不吝赐教,感谢支持。 💬文章目录 一.list容器基本概念二.list容器的常用操作list构造函数list迭代器获取list特性操作list元素操作list赋值操作list的交换、反转、排序、归并操作…
安装win版本的neo4j(2023最新版本)
安装win版本的neo4j 写在最前面安装 win版本的neo4j1. 安装JDK2.下载配置环境变量(也可选择直接点击快捷方式,就可以不用配环境了)3. 启动neo4j 测试代码遇到的问题及解决(每次环境都太离谱了,各种问题)连接…
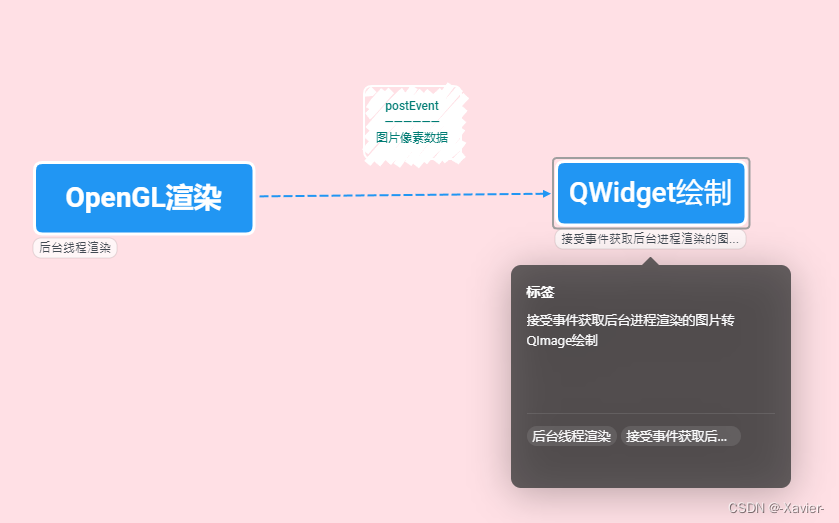
Qt中postevent造成内存泄漏问题的通用解决方案
在Qt中由QCoreApplication统一管理Qt事件的收发和销毁,其中sendEvent为阻塞式发送,用于单线程的事件发送;postevent为非阻塞式发送,构造事件的线程和接受事件的线程可以为两个线程。
最近在做一个个人项目ShaderLab 需要绘制OpenGL实时渲染的图像,由于OpenGL渲染基本都放…
如何提高接口测试覆盖率?
接口测试是测试系统组件间接口的一种测试。
接口测试主要用于检测外部系统与系统之间以及内部各个子系统之间的交互点。
测试的重点是要检查数据的交换,传递和控制管理过程,以及系统间的相互逻辑依赖关系等。
接口测试该如何提高测试的覆盖率呢&#…




![LeetCode[面试题04.08]首个共同祖先](https://img-blog.csdnimg.cn/fa456d6b84b74e70bf46cd0cb7f450f4.png)