本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/90007.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
微服务-gateway鉴权
文章目录 一、前言二、gateway鉴权1、依赖配置2、编写代码3、GlobalFilter详解3.1、GlobalFilter简介3.2、GlobalFilter自定义执行顺序3.2.1、实现Order接口实现自定义执行顺序 一、前言
网关是介于客户端和服务器端之间的中间层,所有的外部请求都会先经过 网关这一…
从过滤器初识责任链设计模式
下面用的过滤器都是注解方式
可以使用非注解方式,就是去web.xml配置映射关系 上面程序的执行输出是 再加一个过滤器 下面来看一段程序 输出结果 和过滤器是否非常相识 但是上面这段程序存在的问题:在编译阶段已经完全确定了调用关系,如果你想改变他们的调用顺序或者继续添加一…
Xilinx UltraScale架构之可配置逻辑块CLB
目录
一、概览
二、UltraScale架构
2.1 UltraScale/UltraScale特点
2.2 与7系列CLB差异
三、 CLB结构
3.1 LUT
3.2 FF
3.3 多路选择器Multiplexers
3.4 进位链Carry Chain
四、应用
4.1 分布式RAM
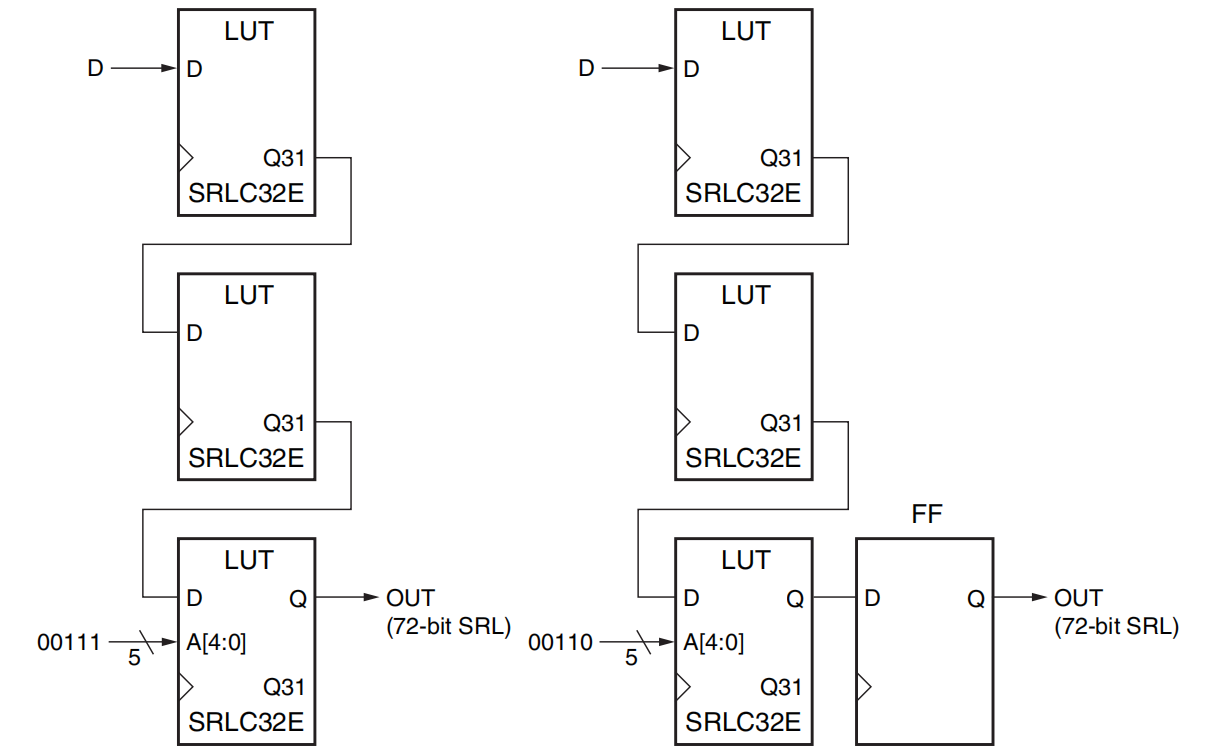
4.2 移位寄存器
4.3 进位链Carry Chain
五、参考资料 一、概览 二…
【Django】让SQLite数据库中表名支持重命名的方法
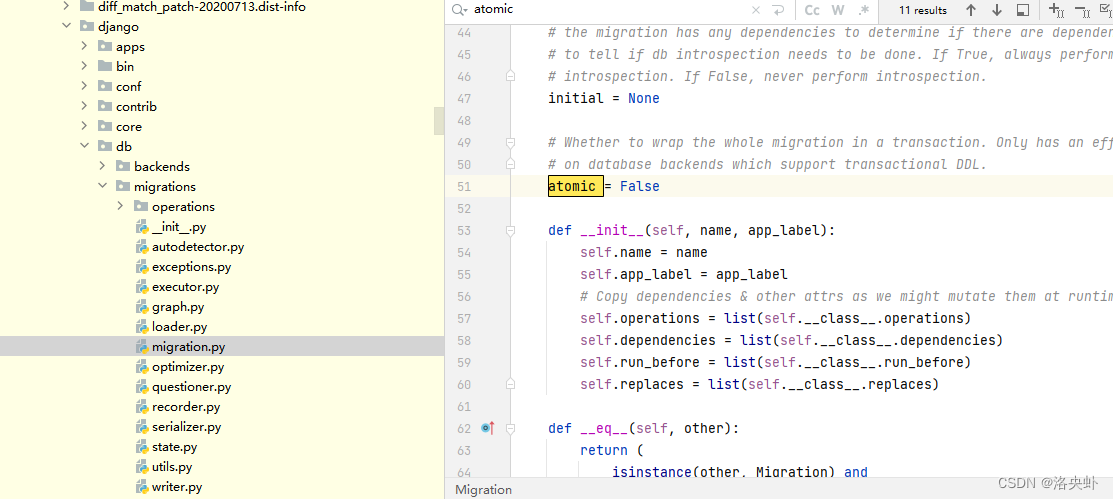
修改了数据库表名之后,更新数据库时跳错:
django.db.utils.NotSupportedError: Renaming the japi_api_info table while in a transaction is not supported on SQLite < 3.26 because it would break referential integrity. Try adding atomic F…
C++面试题(期)-数据库(二)
目录
1.3 事务
1.3.1 说一说你对数据库事务的了解
1.3.2 事务有哪几种类型,它们之间有什么区别?
1.3.3 MySQL的ACID特性分别是怎么实现的?
1.3.4 谈谈MySQL的事务隔离级别
1.3.5 MySQL的事务隔离级别是怎么实现的?
1.3.6 事…
stable diffusion实践操作-hypernetworks
系列文章目录
本文专门开一节写hypernetworks的内容,在看之前,可以同步关注: stable diffusion实践操作 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、h…
线上问诊:数仓开发(二)
系列文章目录
线上问诊:业务数据采集 线上问诊:数仓数据同步 线上问诊:数仓开发(一) 线上问诊:数仓开发(二) 文章目录 系列文章目录前言一、DWS1.最近1日汇总表1.交易域医院患者性别年龄段粒度问诊最近1日汇总表2.交易域医院患者…
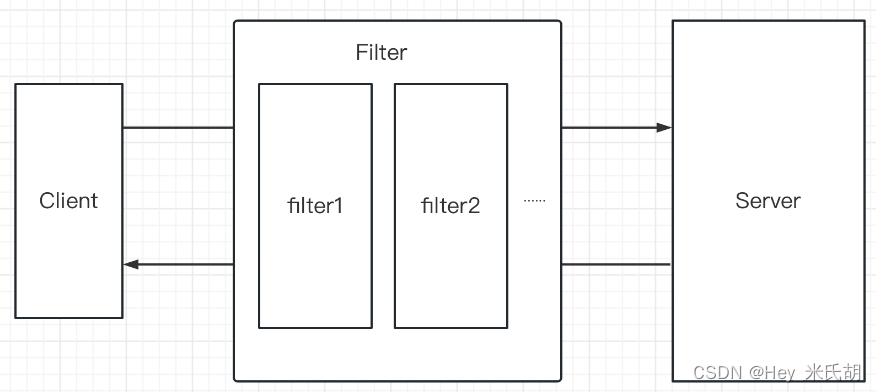
过滤器的应用-Filter
过滤器
1.工作原理 2.创建Filter
2.1通过注解的方式实现
//创建一个类,实现Filter接口
WebFilter(urlPatterns "/myfilter") //urlPatterns表示需要拦截的路径
public class MyFilter implements Filter {Overridepublic void doFilter(ServletReques…
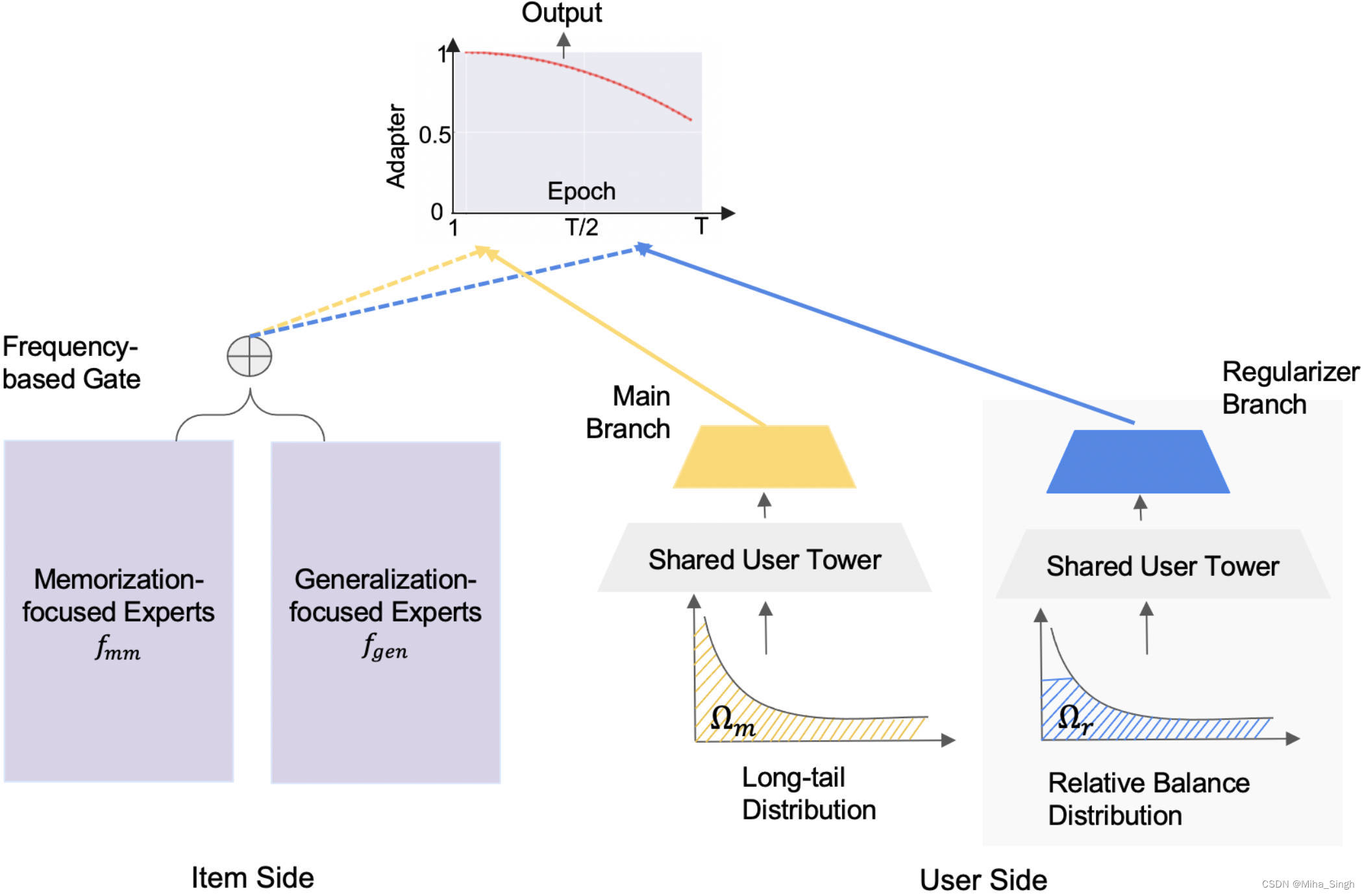
Empowering Long-tail Item Recommendation through Cross Decoupling Network (CDN)
Empowering Long-tail Item Recommendation through Cross Decoupling Network (CDN)
来源:
KDD’2023Google Research 文章目录 Empowering Long-tail Item Recommendation through Cross Decoupling Network (CDN)长尾问题分析CDNItem Memorization and General…
【爬虫小知识】如何利用爬虫爬网页——python爬虫
前言
网络时代的到来,给我们提供了海量的信息资源,但是,想要获取这些信息,手动一个一个网页进行查找,无疑是一项繁琐且效率低下的工作。这时,爬虫技术的出现,为我们提供了一种高效的方式去获取…
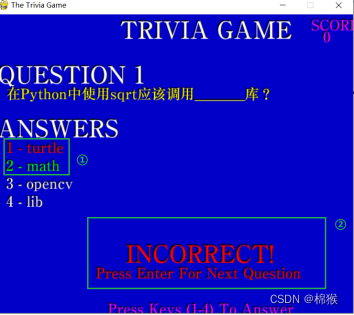
Pygame中Trivia游戏解析6-4
3.3.3 显示题目选项
在显示题目选项时,有三种情况:分别是用户还未选择答案时;用户的答案是正确时;用户的答案是错误时。
(1)用户还未选择答案时
此时,用白色显示四个备选答案,如图…
Leetcode 面试题 17.01 不用加号的加法
设计一个函数把两个数字相加。不得使用 或者其他算术运算符。
示例:
输入: a 1, b 1
输出: 2 提示:
a, b 均可能是负数或 0结果不会溢出 32 位整数
我的答案:
一、信息
1.设计一个函数把两个数相加
2.不得使用或者其他运算符
3.a,b均为负数或…
【管理运筹学】第 7 章 | 图与网络分析(1,图论背景以及基本概念、术语)
文章目录 引言一、图与网络的基本知识1.1 图与网络的基本概念1.1.1 图的定义1.1.2 图中相关术语1.1.3 一些特殊图类1.1.4 图的运算 写在最后 引言
按照正常进度应该学习动态规划了,但我想换换口味,而且动态规划听说也有一定难度,还不一定会考…
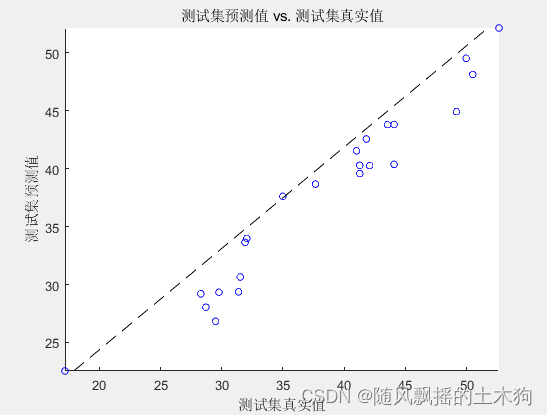
【MATLAB第71期】基于MATLAB的Abcboost自适应决策树多输入单输出回归预测及多分类预测模型(更新中)
【MATLAB第71期】基于MATLAB的Abcboost自适应决策树多输入单输出回归预测及多分类预测模型(更新中)
一、效果展示(多分类预测) 二、效果展示(回归预测) 三、代码获取
CSDN后台私信回复“71期”即可获取下…
Android 1.1 背景相关与系统架构分析
目录 1.1 背景相关与系统架构分析
分类 Android 基础入门教程
1.Android背景与当前的状况 2.Android系统特性与平台架构
系统特性:
平台架构图:
架构的简单理解:
3.本节小结: 1.1 背景相关与系统架构分析
分类 Android 基础…
阻塞/非阻塞、同步/异步(网络IO)
1.阻塞/非阻塞、同步/异步(网络IO) 【思考】典型的一次 IO 的两个阶段是什么? 数据就绪 和 数据读写 数据就绪 :根据系统 IO 操作的就绪状态 阻塞 非阻塞 数据读写 :根据应用程序和内核的交互方式 同步 异步 陈硕:在处理 IO …
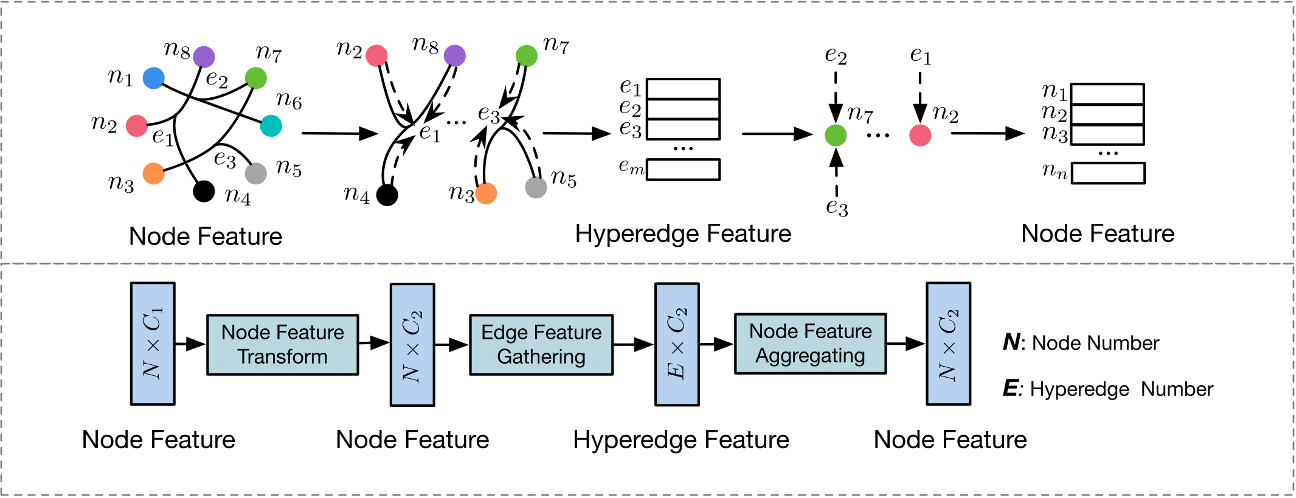
超图嵌入论文阅读2:超图神经网络
超图嵌入论文阅读2:超图神经网络 原文:Hypergraph Neural Networks ——AAAI2019(CCF-A) 源码:https://github.com/iMoonLab/HGNN 500star 概述
贡献:用于数据表示学习的超图神经网络 (HGNN) 框架…
英码科技受邀亮相2023WAIE物联网与人工智能展,荣获行业优秀创新力产品奖!
8月28日-30日,2023WAIE 物联网与人工智能展在深圳福田会展中心顺利举办。英码科技受邀亮相本届展会,并现场重点展出了面向智慧交通、智慧校园、智慧应急、智慧园区等不同行业的创新AIoT产品、AI技术服务等内容,与生态伙伴积极探讨市场需求和问…
2020ICPC南京站
K
K Co-prime Permutation
题意:给定n和k,让你构造n的排列,满足gcd(pi, i)1的个数为k。
思路:因为x和x-1互质,1和任何数互质,任何数和它本身不互质
当k为奇数时,p11,后面k-1个数…