本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/138315.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
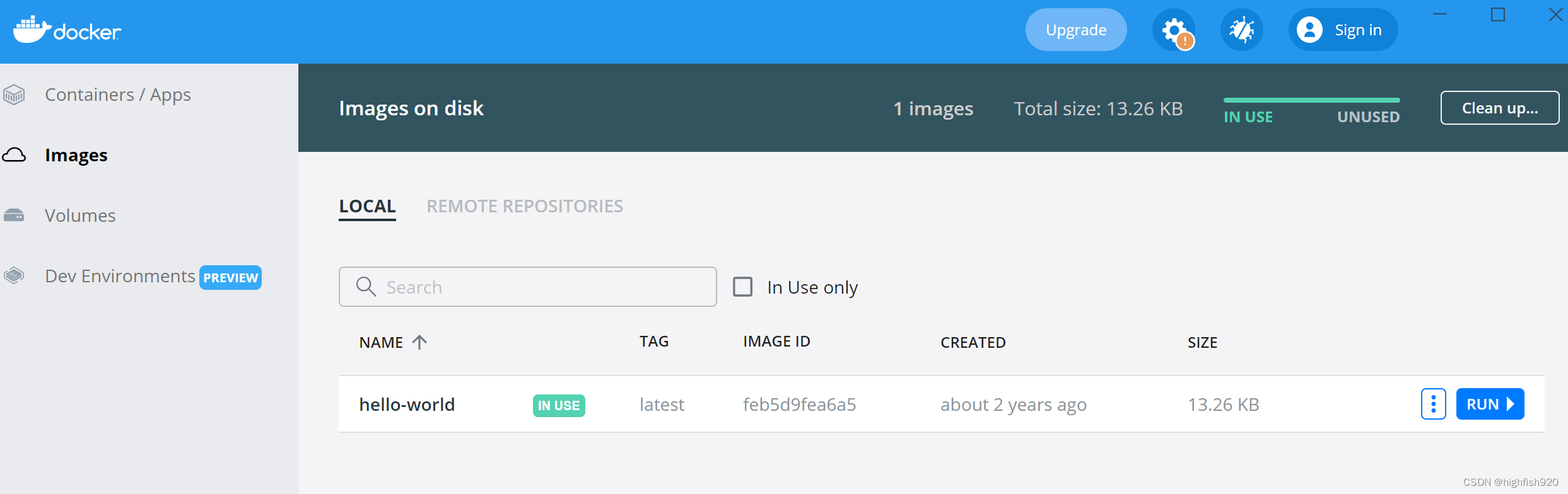
Docker-Windows安装使用
1.下载docker
https://cr.console.aliyun.com/cn-hangzhou/instances/mirrors
2.配置虚拟化环境
通过控制面板“设置”启用 Hyper-V 角色
右键单击 Windows 按钮并选择“应用和功能”。选择相关设置下右侧的“程序和功能”。选择“打开或关闭 Windows 功能”。选择“Hyper-…
节日灯饰灯串灯出口欧洲CE认证办理
灯串(灯带),这个产品的形状就象一根带子一样,再加上产品的主要原件就是LED,因此叫做灯串或者灯带。2022年,我国灯具及相关配件产品出口总额超过460亿美元。其中北美是最大的出口市场。其次是欧洲市场&#…
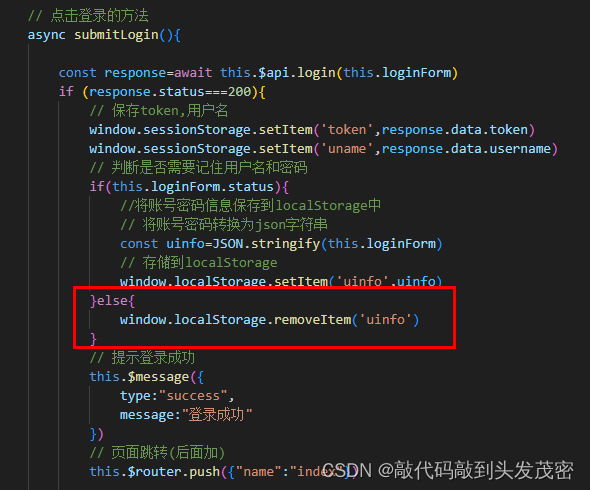
平台登录页面实现(一)
文章目录 一、实现用户名、密码、登录按钮、记住用户表单1、全局css代码定义在asserts/css/global.css 二、用户名、密码、记住用户的双向绑定三、没有用户,点击注册功能实现四、实现输入用户名、密码、点击登录按钮进行登录操作五、实现表单项校验六、提交表单预验…
git报错:Failed to connect to 127.0.0.1 port 1080
Bug描述 由于在试了网上的这条命令
git config --global http.proxy socks5 127.0.0.1:1080
git config --global https.proxy socks5 127.0.0.1:1080git config --global http.proxy 127.0.0.1:1080
git config --global https.proxy 127.0.0.1:1080Bug描述:Faile…
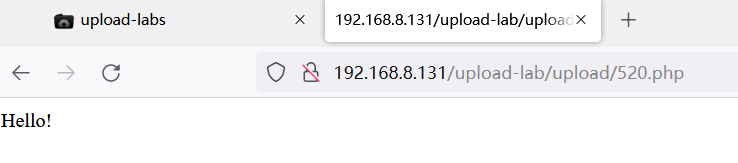
《Upload-Labs》01. Pass 1~13
Upload-Labs 索引前言Pass-01题解 Pass-02题解总结 Pass-03题解总结 Pass-04题解 Pass-05题解总结 Pass-06题解总结 Pass-07题解总结 Pass-08题解总结 Pass-09题解 Pass-10题解 Pass-11题解 Pass-12题解总结 Pass-13题解 靶场部署在 VMware - Win7。 靶场地址:https…
性格孤僻怎么办?改变性格孤僻的4种方法
性格孤僻是比较常见的说法,日常中我们说某人性格孤僻,意思就是这人不太合群,喜欢独来独往,话少,人际关系不太好,其言行往往不符合大众的价值观。从性格孤僻的角度来看,可能跟很多种心理疾病存在…
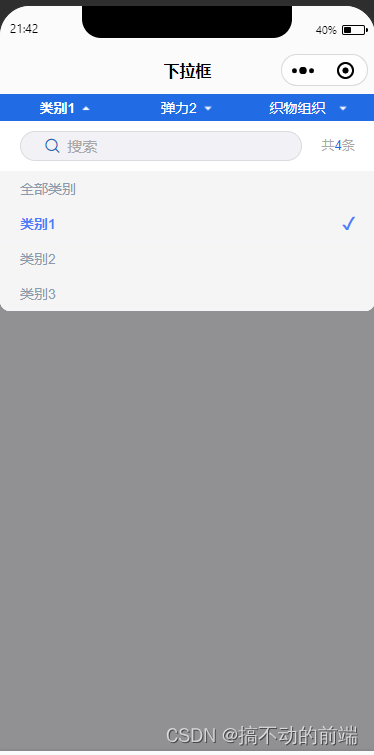
uniapp 实现下拉筛选框 二次开发定制
前言
最近又收到了一个需求,需要在uniapp 小程序上做一个下拉筛选框,然后找了一下插件市场,确实有找到,但不过他不支持搜索,于是乎,我就自动动手,进行了二开定制,站在巨人的肩膀上&…
经历网 微信二维码 制作方法
1、谷歌浏览器,打开要制作微信二维码的 网站页面
2、点击页面空白处(此步为了使鼠标激活页面,可省),点击鼠标右键,弹窗 点选 为此页面创建二维码,点击下载到自己指定的地方。完成。
下载下来的…
【前段基础入门之】=>CSS 常用的字体文本属性
导读: 这一章,主要分享一些 CSS 中的一些,常用的 字体和文本方面的属性。 文章目录 字体属性字体大小字体族字体风格字体粗细字体复合写法 文本属性文本间距文本修饰文本缩进文本水平对齐行高vertical-align 字体属性
字体大小
属性名&…
inndy_echo
inndy_echo
Arch: i386-32-little
RELRO: Partial RELRO
Stack: No canary found
NX: NX enabled
PIE: No PIE (0x8048000)32位,只开了NX
int __cdecl __noreturn main(int argc, const char **argv, const char **envp)
{char s; // [espCh…
麒麟信安服务器操作系统V3.5.2重磅发布!
9月25日,麒麟信安基于openEuler 22.03 LTS SP1版本的商业发行版——麒麟信安服务器操作系统V3.5.2正式发布。
麒麟信安服务器操作系统V3定位于电力、金融、政务、能源、国防、工业等领域信息系统建设,以安全、稳定、高效为突破点,满足重要行…
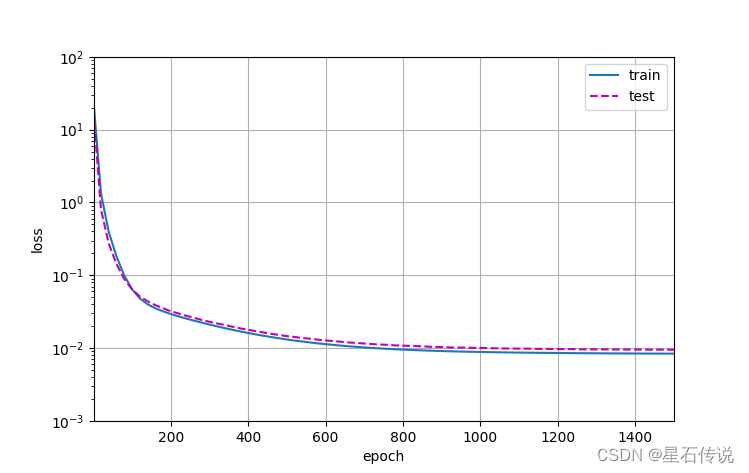
深度学习——模型选择、欠拟合和过拟合
深度学习——模型选择、欠拟合和过拟合 文章目录 前言一、训练误差和泛化误差1.1. 统计学习理论1.2. 模型复杂性 二、模型选择2.1. 验证集2.2. K折交叉验证 三、欠拟合 or 过拟合3.1. 模型复杂性3.2. 数据集大小 四、多项式回归4.1. 生成数据集4.2. 对模型进行训练和测试4.3. 三…
Elastic SQL 输入:数据库指标可观测性的通用解决方案
作者:Lalit Satapathy, Ishleen Kaur, Muthukumar Paramasivam Elastic SQL 输入(metricbeat 模块和输入包)允许用户以灵活的方式对许多支持的数据库执行 SQL 查询,并将结果指标提取到 Elasticsearch。 本博客深入探讨了通用 SQL …
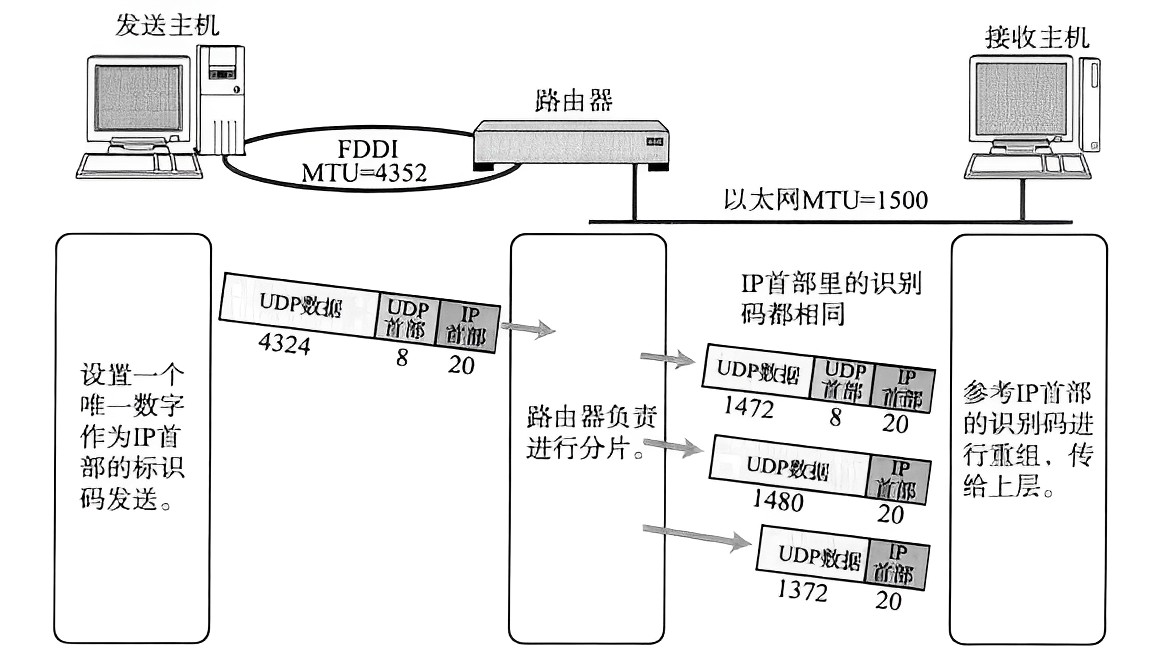
数据链路层 MTU 对 IP 协议的影响
在介绍主要内容之前,我们先来了解一下数据链路层中的"以太网" 。
“以太网”不是一种具体的网络,而是一种技术标准;既包含了数据链路层的内容,也包含了一些物理层的内容。
下面我们再来了解一下以太网数据帧ÿ…
Transformers.js v2.6 现已发布
🤯 新增了 14 种架构 在这次发布中,我们添加了大量的新架构:BLOOM、MPT、BeiT、CamemBERT、CodeLlama、GPT NeoX、GPT-J、HerBERT、mBART、mBART-50、OPT、ResNet、WavLM 和 XLM。这将支持架构的总数提升到了 46 个!以下是一些示例…
ubuntu20安装nvidia驱动
1. 查看显卡型号
lspci | grep -i nvidia
我的输出:
01:00.0 VGA compatible controller: NVIDIA Corporation GP104 [GeForce GTX 1080] (rev a1)
01:00.1 Audio device: NVIDIA Corporation GP104 High Definition Audio Controller (rev a1)
07:00.0 VGA comp…
stable diffusion模型评价框架
GhostReview:全球第一套AI绘画ckpt评测框架代码 - 知乎大家好,我是_GhostInShell_,是全球AI绘画模型网站Civitai的All Time Highest Rated (全球历史最高评价) 第二名的GhostMix的作者。在上一篇文章,我主要探讨自己关于ckpt的发展方向的观点…
测试用例的编写(面试常问)
作者:爱塔居 专栏:软件测试 作者简介:不断总结,才能变得更好~踩过的坑,不能再踩~ 文章简介:常见的几个测试用例。 一、淘宝购物车 二、登录页面 三、三角形测试用例
abc结果346普通三角形333等边三角形334…
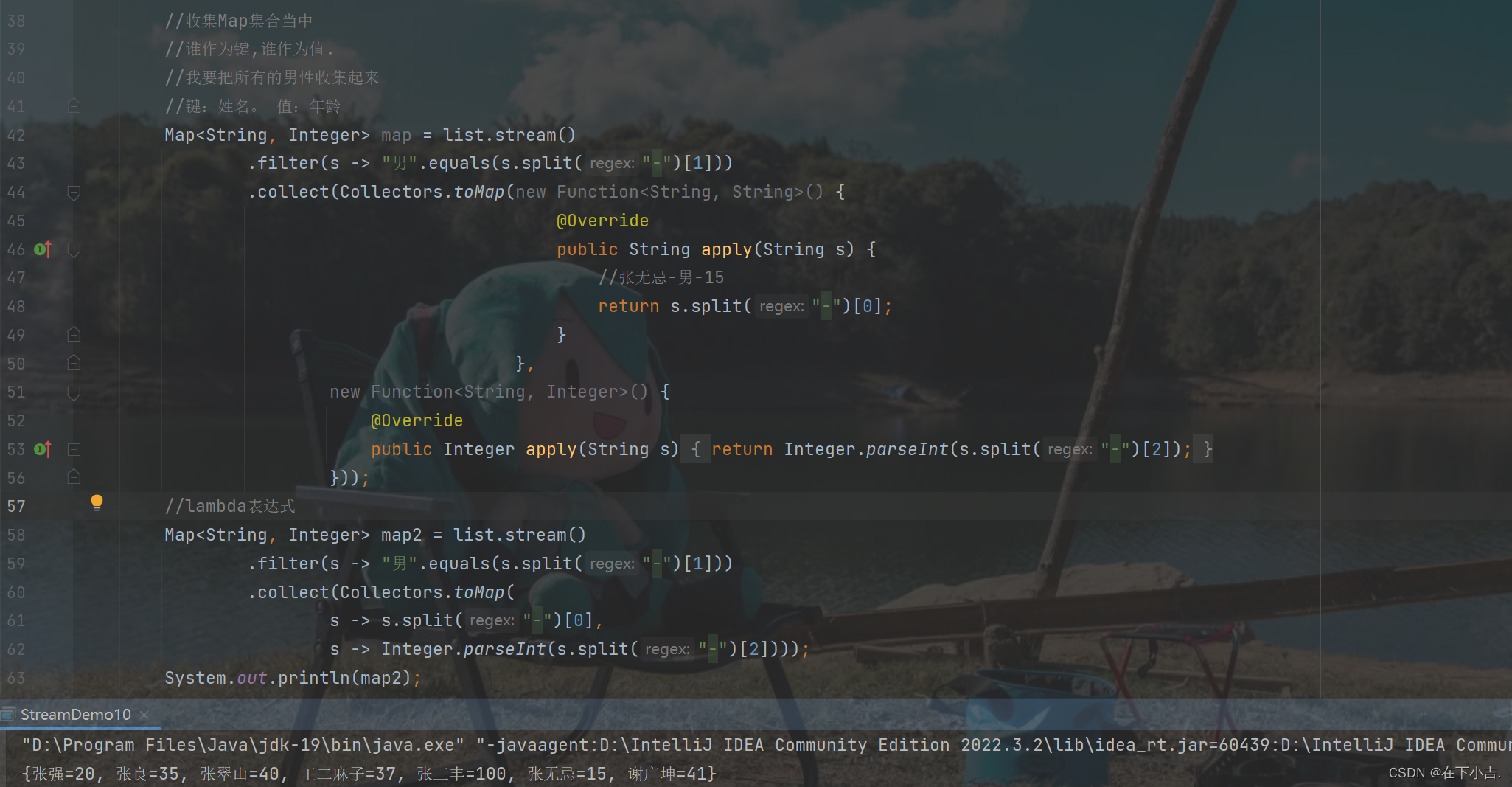
【从入门到起飞】JavaSE—Stream流
🎊专栏【JavaSE】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【如愿】 🥰欢迎并且感谢大家指出我的问题 文章目录 🍔Stream流的作用🍔Stream流的使用步骤🎄获取Strea…