本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/430564.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
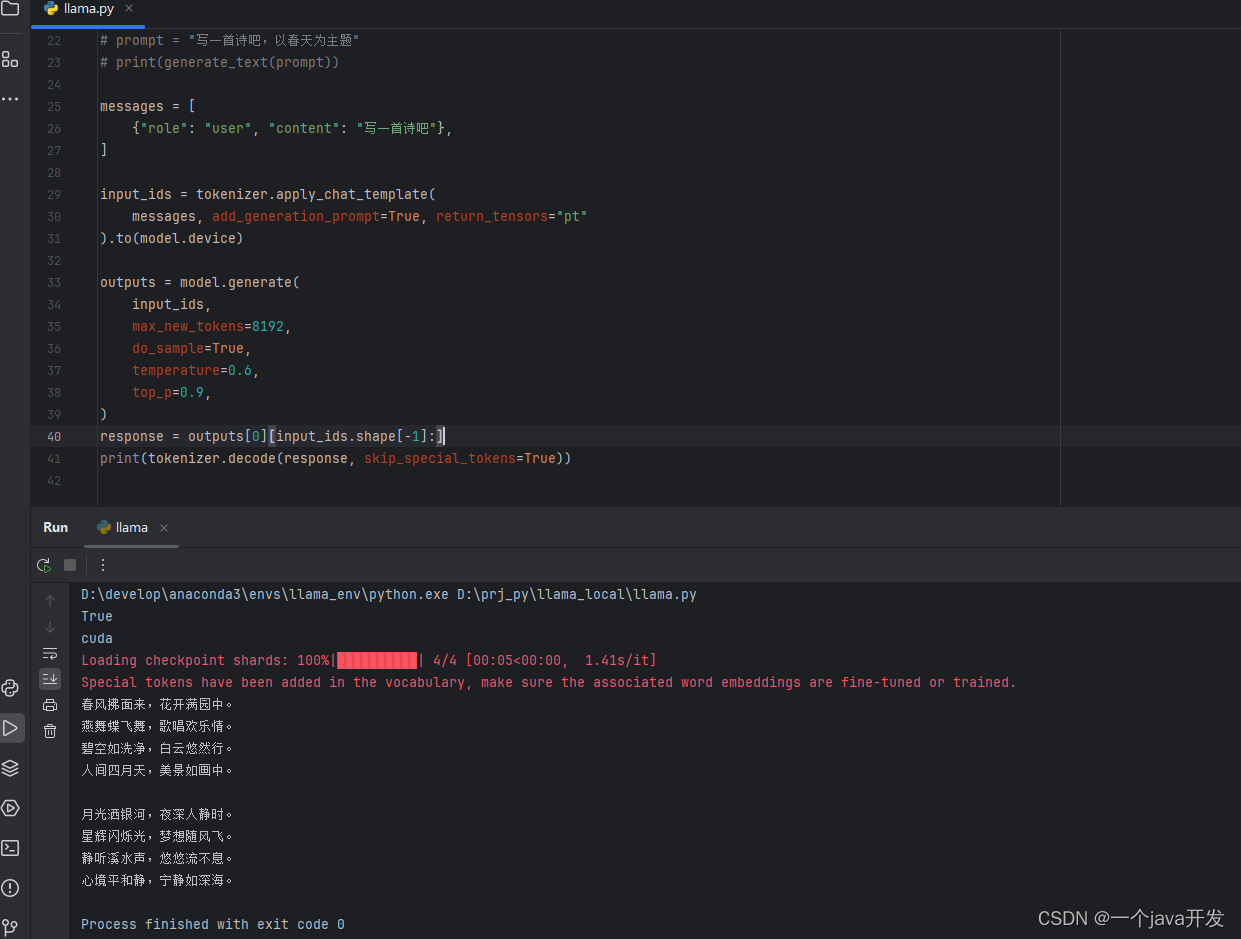
LLAMA3==shenzhi-wang/Llama3-8B-Chinese-Chat。windows安装不使用ollama
创建环境:
conda create -n llama3_env python3.10 conda activate llama3_env conda install pytorch torchvision torchaudio cudatoolkit11.7 -c pytorch
安装Hugging Face的Transformers库:
pip install transformers sentencepiece 下载模型
ht…
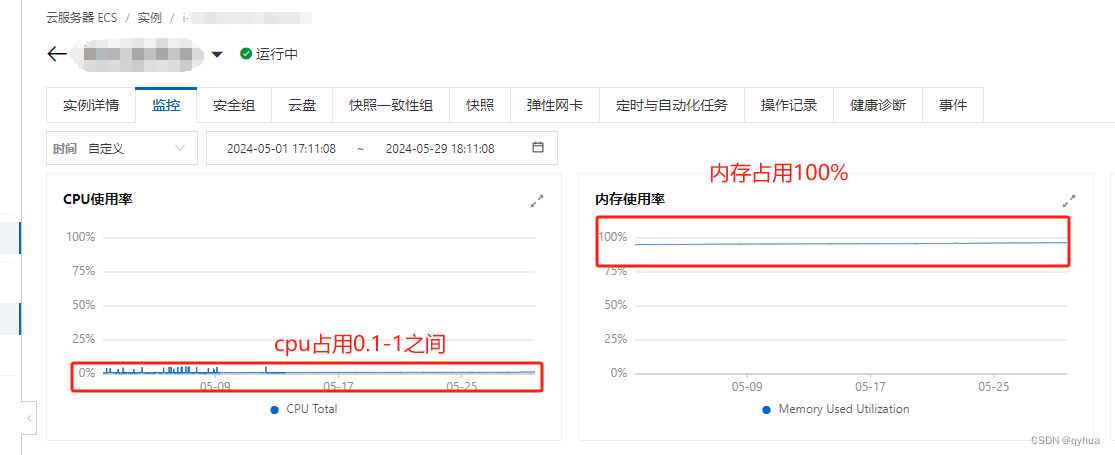
服务器内存与CPU要占用多少才合理?
一 通常服务器内存占用多少合理?cpu占用多少才合理? 1 通常配置范围建议:
建议CPU使用率不高于80%;内存使用率不高于80%; 注意:具体情况还需要根据服务器的实际负载和应用场景来判断。 2 内存使用率&…
景源畅信电商:抖音开店步骤是什么?
随着社交媒体的兴起,抖音已经成为一个不可忽视的电商平台。许多人都希望通过抖音开店来实现自己的创业梦想。那么,抖音开店的具体步骤是什么呢?接下来,我们将详细阐述这一问题。 一、明确回答问题抖音开店的步骤主要包括:注册账号…
Java基础20(文件操作 IO流 InputStream字节输入流 OutputStream字节输出流 Writer 字符输出流)
目录
一、File 文件对象
1. 创建对象
2. 相对路径和绝对路径
3. 一些方法
汇总:
获取文件信息1:
判断文件:
删除文件:
创建文件:
获取文件信息2:
4. 小结
二、IO流
1. InputStream字节输入流 …
LPDDR6带宽预计将翻倍增长:应对低功耗挑战与AI时代能源需求激增
在当前科技发展的背景下,低能耗问题成为了业界关注的焦点。国际能源署(IEA)近期报告显示,日常的数字活动对电力消耗产生显著影响——每次Google搜索平均消耗0.3瓦时(Wh),而向OpenAI的ChatGPT提出的每一次请求则消耗2.9…
利用C++与Python调用千帆免费大模型,构建个性化AI对话系统
千帆大模型已于2024年4月25日正式免费,调用这个免费的模型以实现自己的AI对话功能,遵循以下步骤:
了解千帆大模型:
千帆大模型是百度智能云推出的一个平台,提供了一系列AI能力和工具,用于快速开发和应用A…
【busybox记录】【shell指令】rmdir
目录
内容来源:
【GUN】【rmdir】指令介绍
【busybox】【rmdir】指令介绍
【linux】【rmdir】指令介绍
使用示例:
删除空目录 - 默认
删除dirname下的所有空目录,包括因删除其他目录而变为空的目录
常用组合指令:
指令不…
在做题中学习(62):矩阵区域和
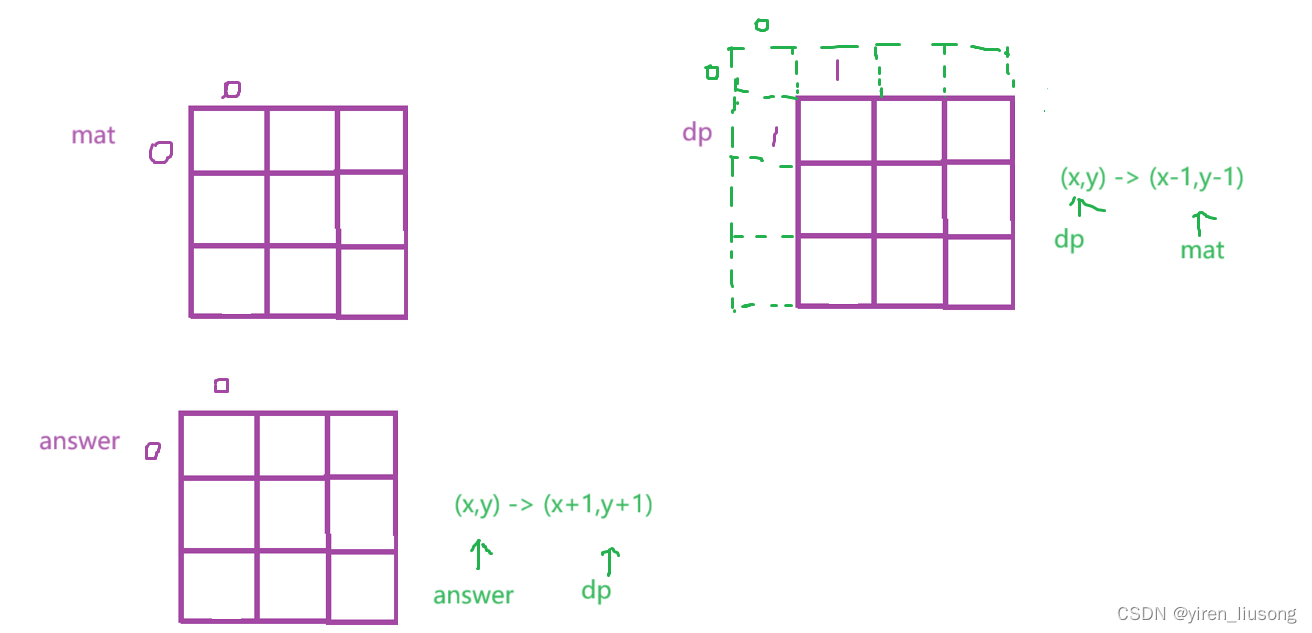
1314. 矩阵区域和 - 力扣(LeetCode) 解法:二维前缀和
思路:读题画图才能理解意思:dun点点的是mat中的一个数,而要求的answer同位置的数 以点为中心上下左右延长 k 个单位所围成长方形的和。 因为最后answ…
前端学习--React部分
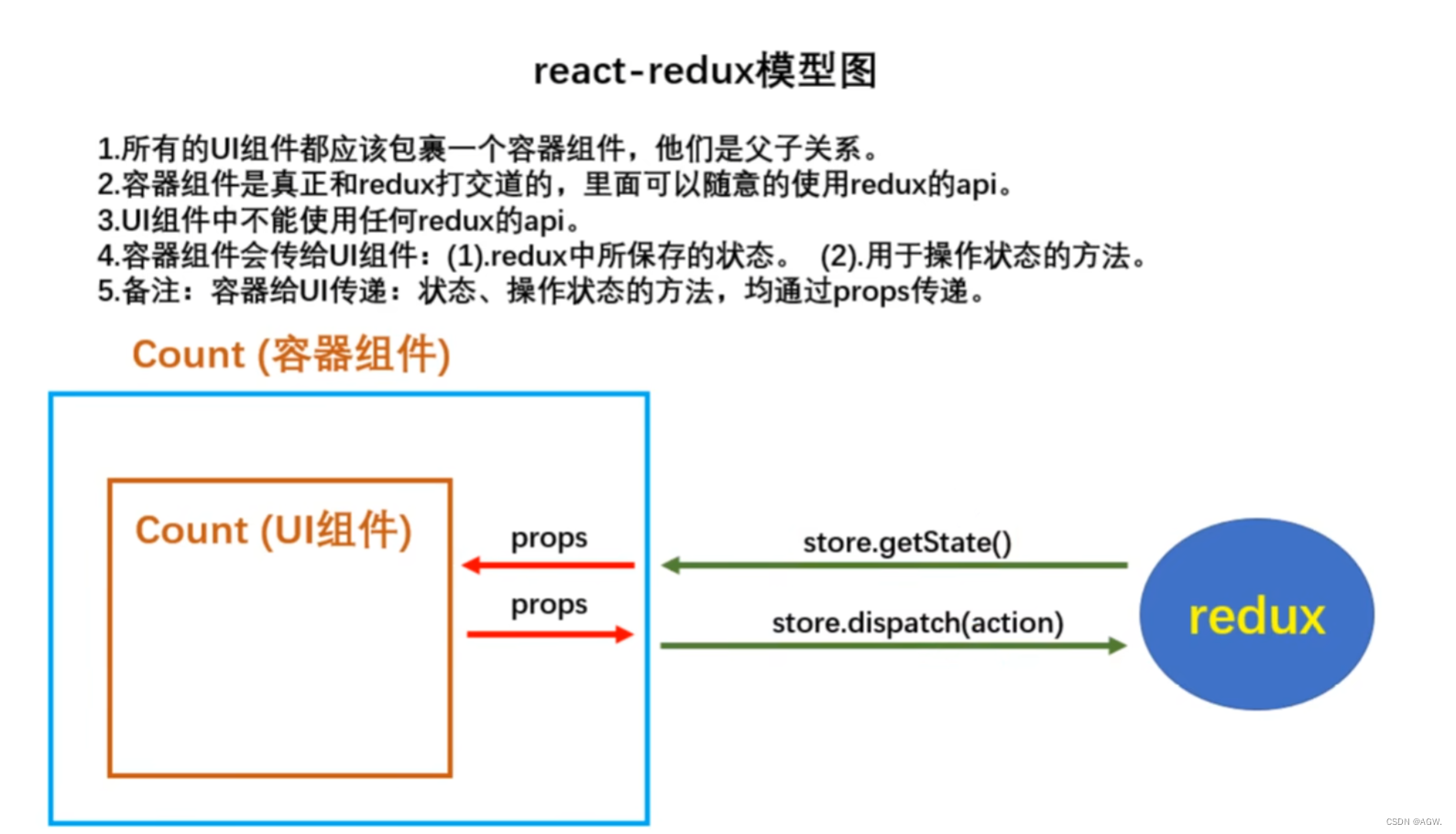
文章目录 前端学习--React部分前言1.React简介1.1React的特点1.2引入文件1.3JSX🍉JSX简介与使用🍉JSX语法规则 1.4模块与组件🍉模块🍉组件 1.5安装开发者工具 2.React面向组件编程2.1创建组件🍉函数式组件🍉…
【数据结构:排序算法】堆排序(图文详解)
🎁个人主页:我们的五年
🔍系列专栏:数据结构课程学习
🎉欢迎大家点赞👍评论📝收藏⭐文章 目录
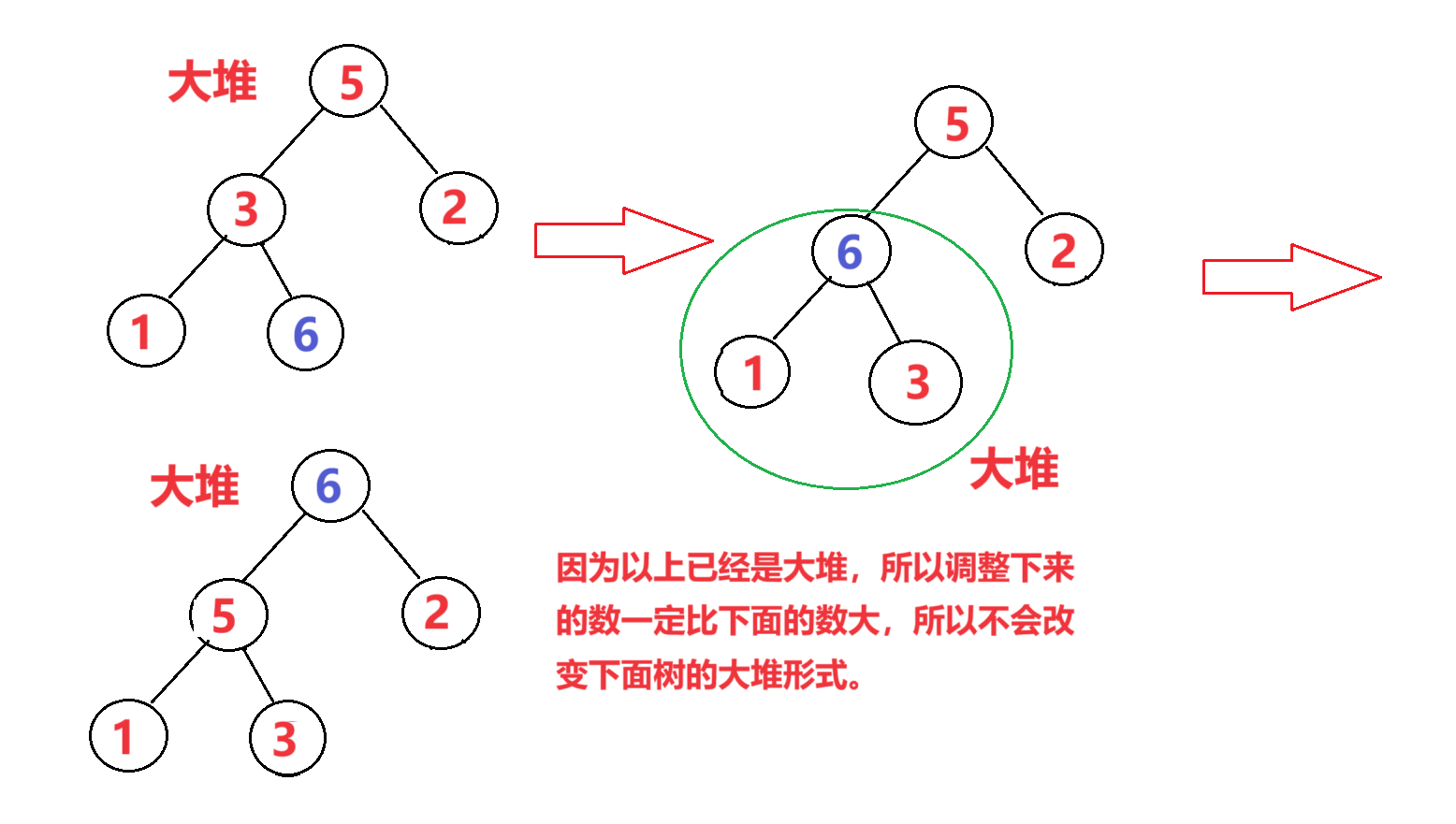
🍩1.大堆和小堆
🍩2.向上调整算法建堆和向下调整算法建堆:…
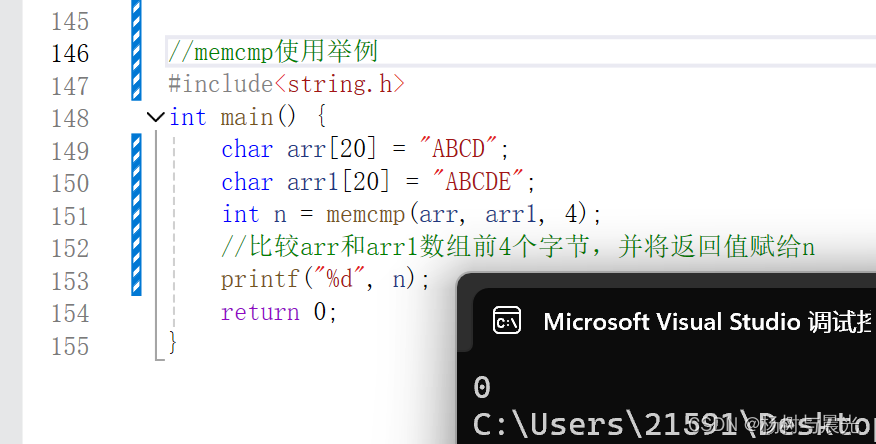
【C++】模拟实现string类
🦄个人主页:修修修也 🎏所属专栏:C ⚙️操作环境:Visual Studio 2022 目录
一.了解项目功能
二.逐步实现项目功能模块及其逻辑详解
🎏构建成员变量
🎏实现string类默认成员函数
📌构造函数
📌析构函数…
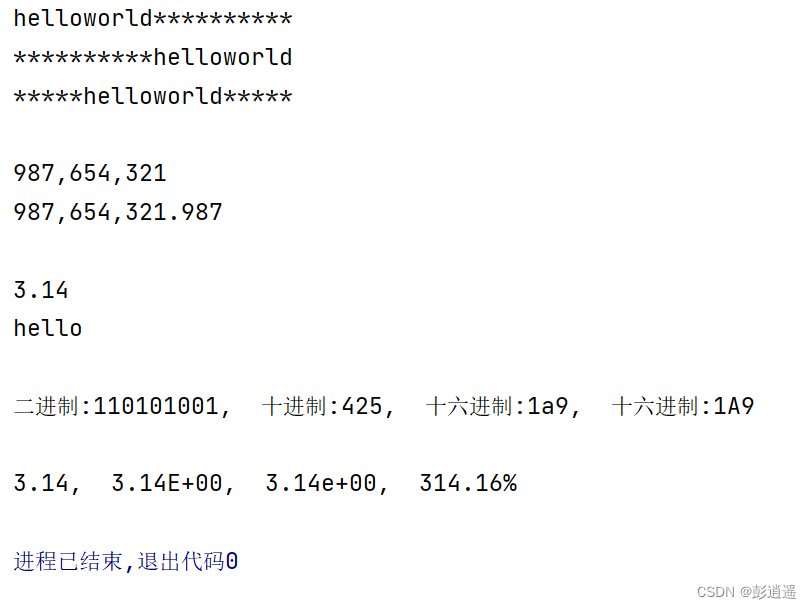
python从0开始学习(十二)
目录 前言
1、字符串的常用操作
2、字符串的格式化
2.1 格式化字符串的详细格式(针对format形式)
编辑
总结 前言 上一篇文章我们讲解了两道关于组合数据类型的题目,本篇文章我们将学习新的章节,学习字符串及正则表达式。 …
SAP 生产订单报工函数BAPI_PRODORDCONF_CREATE_TT不返回报错信息
最近财务一直反馈MES报工的数据都没有成本,然后去查看原因发现是财务当月的KP26的价格没有进行维护,导致没有收集到工单的报工成本。
但是在前台操作CO11 报工的时候,系统会给出报错的信息 但是我们在调用函数BAPI_PRODORDCONF_CREATE_TT的时候,系统并没有返回报错的信息…
【SPSS】基于因子分析法对水果茶调查问卷进行分析
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…
数据库之Mysql提权
MySQL UDF 提权
UDF(user defined function)⽤户⾃定义函数,是 mysql 的⼀个拓展接⼝。⽤户可以通过⾃定义函数实现在mysql中⽆法⽅便实现的功能,其添加的新函数都可以在 sql 语句中调⽤,就像调⽤本机函数⼀样。 先前…
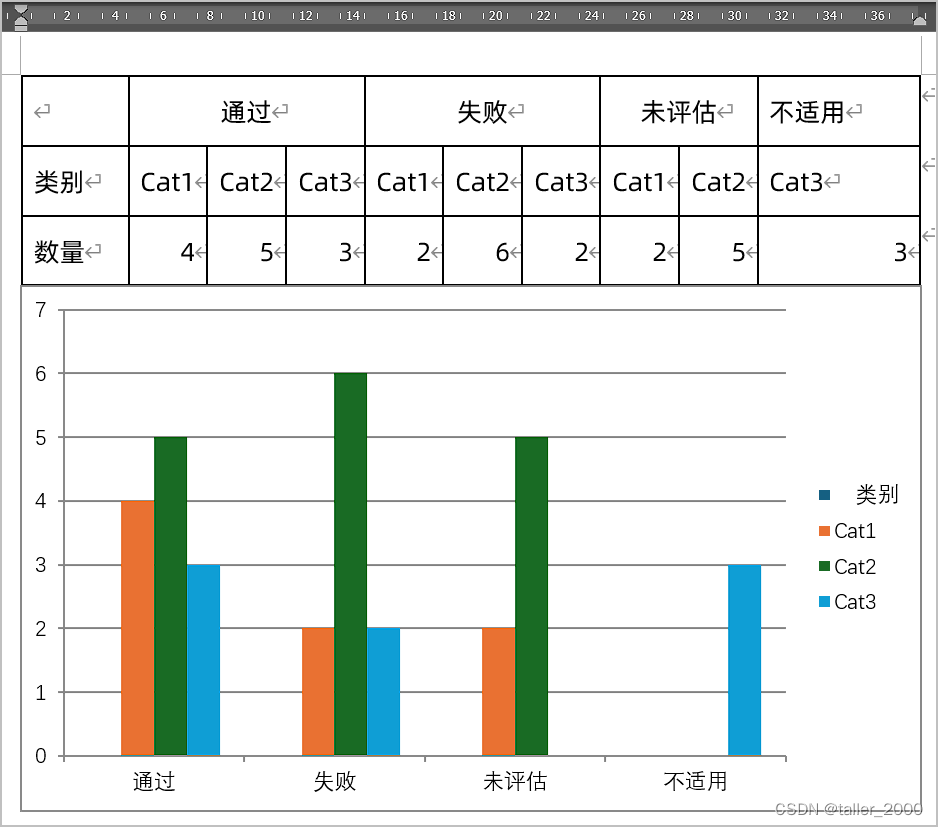
使用Word表格数据快速创建图表
实例需求:Word的表格如下所示,标题行有合并单元格。 现在需要根据上述表格数据,在Word中创建如下柱图。如果数据在Excel之中,那么创建这个图并不复杂,但是Word中就没用那么简单了,虽然Word中可以插入图表&a…
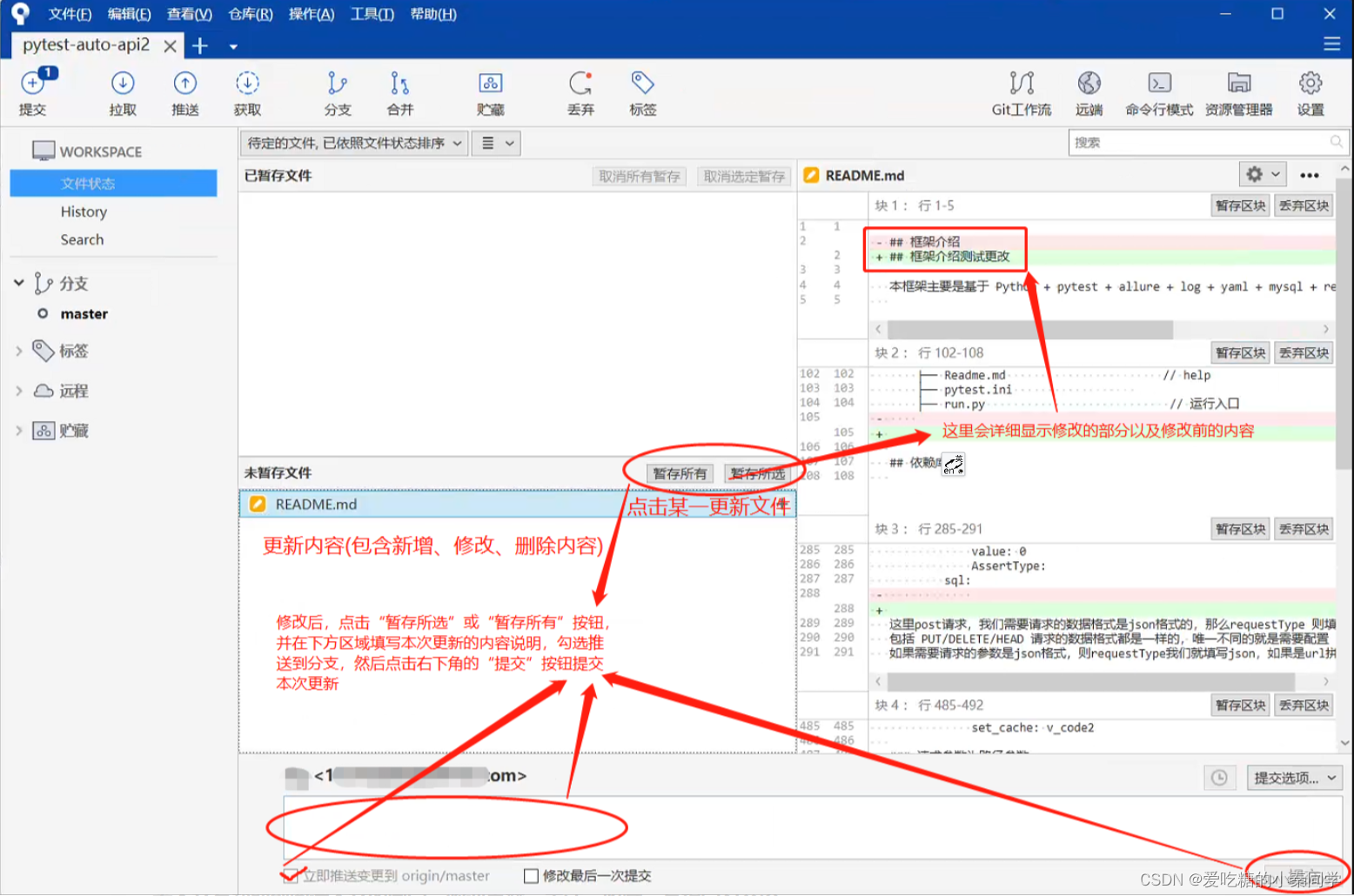
Sourcetree安装教程及使用
1 Sourcetree介绍 Sourcetree是一款免费的Git图形化客户端,它由Atlassian开发,提供了跨平台的支持,可运行在Windows和Mac操作系统上。Sourcetree可以让开发者更方便地使用Git来管理代码,不需要在命令行中输入复杂的Git命令&#x…
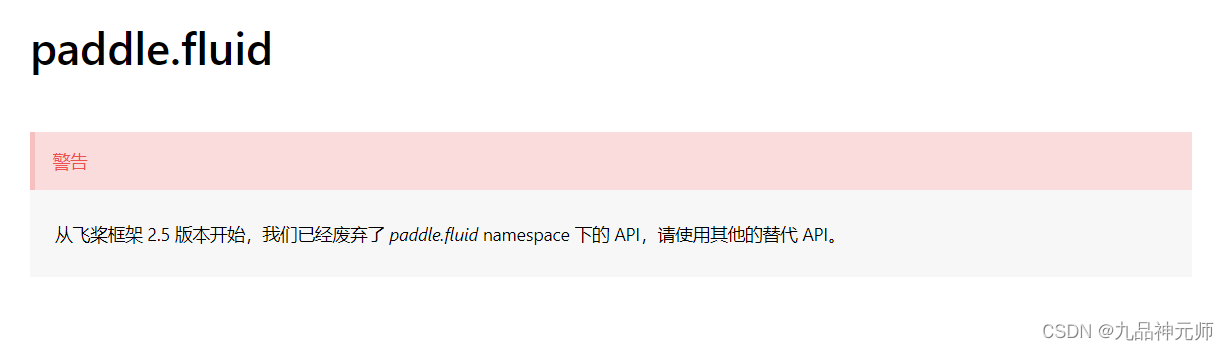
Paddle使用问题No module named ‘paddle.fluid’
这是Paddle版本的问题,从飞桨框架 2.5 版本开始,已经废弃了 paddle.fluid 。
解决方案:修改paddle版本
pip install paddlepaddle2.4.0