本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/430578.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Android数据缓存框架 - 内存数据载体从LiveData到StateFlow
引言:所有成功者的背后,都有一份艰苦的历程,不要只看到了人前的风光,而低估了他们背后所付出的努力。 随着flow到流行度越来越高,有开发者呼吁我使用flow,于是我就如你们所愿,新增了StateFlow作…
深入分析 Android Activity (三)
文章目录 深入分析 Android Activity (三)1. Activity 的配置变化处理1.1 处理配置变化 2. Activity 的存储和恢复状态2.1 保存状态2.2 恢复状态 3. Activity 与 Fragment 的通信3.1 通过接口进行通信3.2 通过 ViewModel 进行通信 4. Activity 的窗口管理和视图层次结构4.1 Dec…
装机必备——截图软件PixPin安装教程
装机必备——截图软件PixPin安装教程
软件下载
软件名称:PixPin 1.5 软件语言:简体中文 软件大小:30.1M 系统要求:Windows7或更高, 64位操作系统 硬件要求:CPU2GHz ,RAM2G或更高 下载通道①迅…
IEEE Latex模版踩雷避坑指南
参考文献 原Latex模版
\begin{thebibliography}{1}
\bibliographystyle{IEEEtran}\bibitem{ref1}
{\it{Mathematics Into Type}}. American Mathematical Society. [Online]. Available: https://www.ams.org/arc/styleguide/mit-2.pdf\bibitem{ref2}
T. W. Chaundy, P. R. Ba…
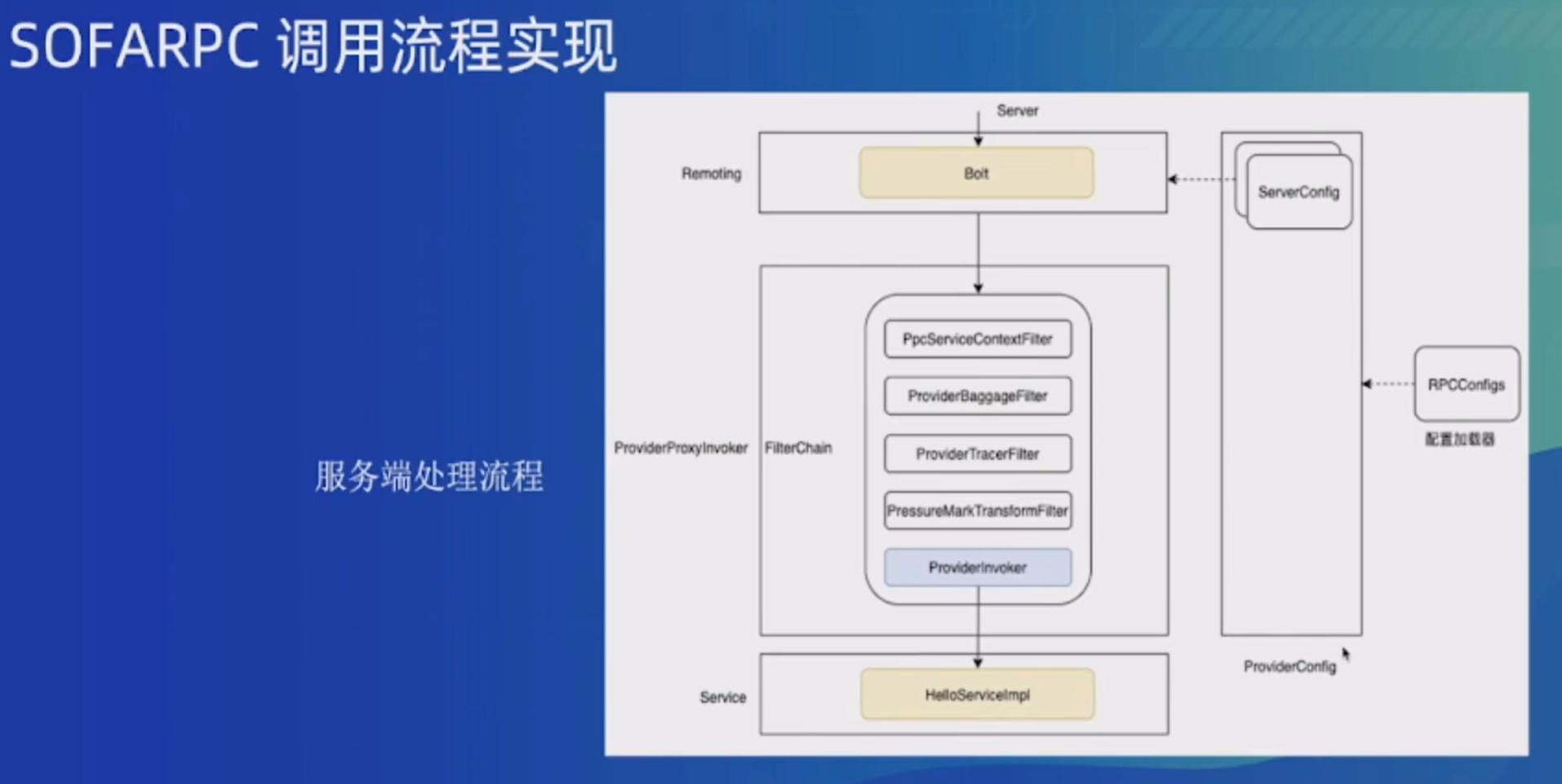
【SOFARPC框架的设计和实现】笔记记录
感谢刘老师对rpc框架的视频讲解:SOFAChannel#31 RPC框架的设计和实现_哔哩哔哩_bilibili 每个扩展点就是一个接口,可以通过实现接口来时拓展。
以registry举例,可以使用Extensible注解标记接口,然后Extension标记方法的实现。 …
[双指针] --- 快乐数 盛最多水的容器
Welcome to 9ilks Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk
(๑•́ ₃ •̀๑) 文章专栏: 算法Journey 本篇博客我们分享一下双指针算法中的快慢指针以及对撞双指针,下面我们开始今天的学习吧~ 🏠 快乐数 📒 题…
WAF几种代理模式详解
WAF简介 WAF的具体作用就是检测web应用中特定的应用,针对web应用的漏洞进行安全防护,阻止如SQL注入,XSS,跨脚本网站攻击等
正向代理 WAF和客户端与网络资源服务器都建立连接,但是WAF 的工作口具有自己的 IP 地址&…
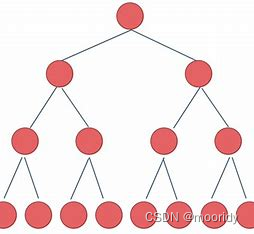
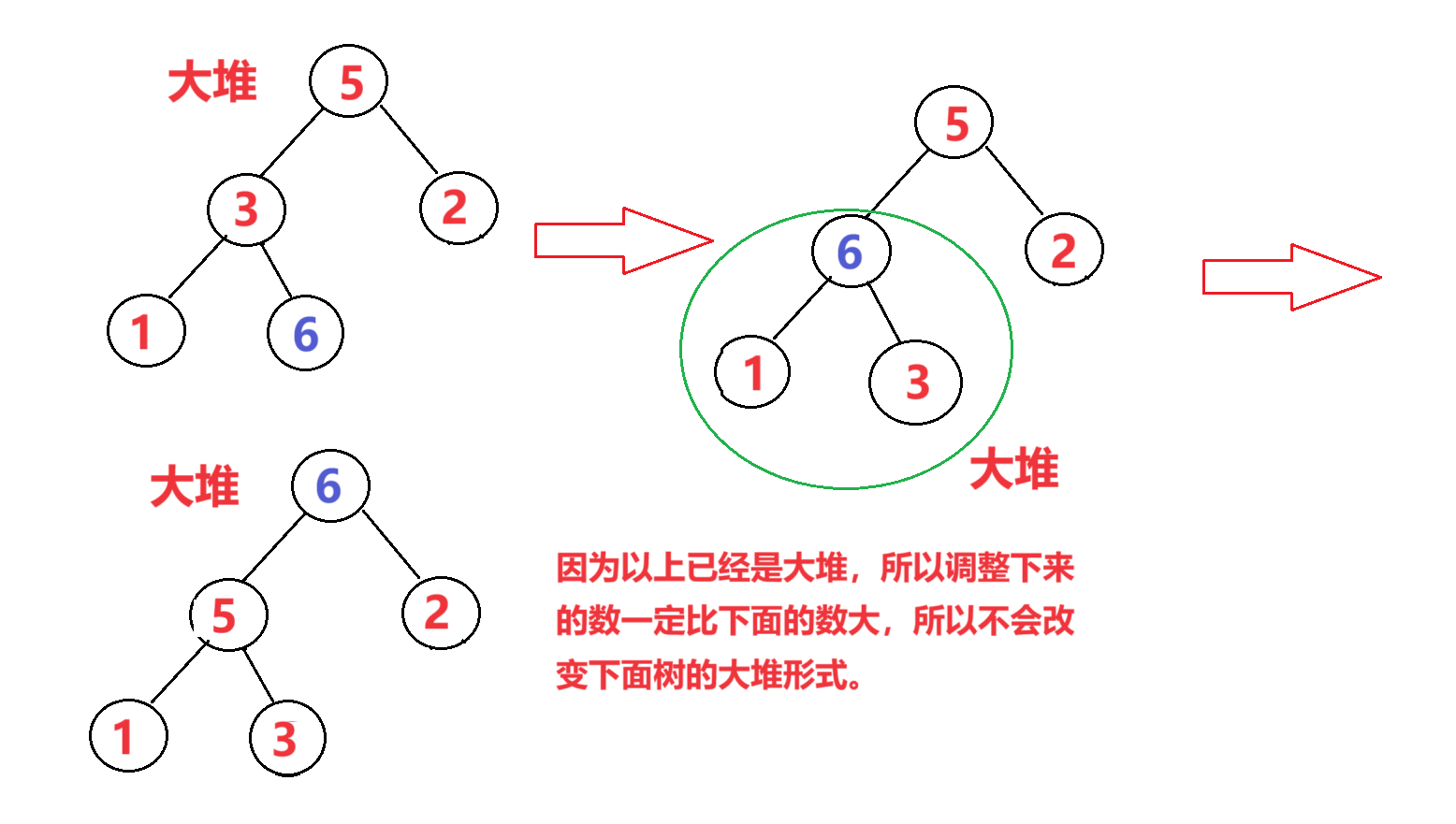
数据结构 | 详解二叉树——堆与堆排序
🥝堆 堆总是一棵完全二叉树。 大堆:父节点总是大于子节点。 小堆:父节点总是小于子节点。 注意:1.同一个节点下的两个子节点并无要求先后顺序。 2.堆可以是无序的。
🍉堆的实现
🌴深度剖析
1.父节点和子…
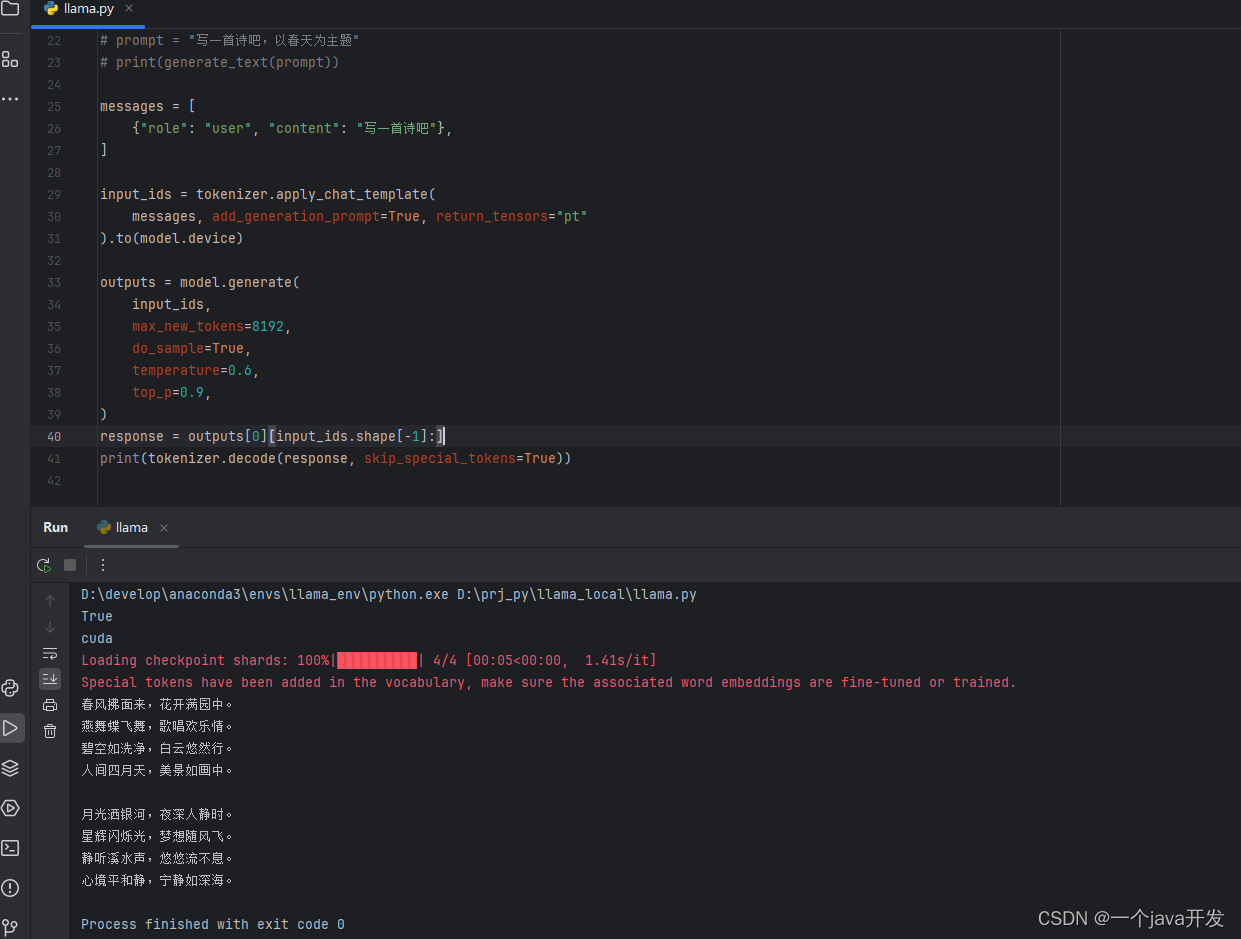
LLAMA3==shenzhi-wang/Llama3-8B-Chinese-Chat。windows安装不使用ollama
创建环境:
conda create -n llama3_env python3.10 conda activate llama3_env conda install pytorch torchvision torchaudio cudatoolkit11.7 -c pytorch
安装Hugging Face的Transformers库:
pip install transformers sentencepiece 下载模型
ht…
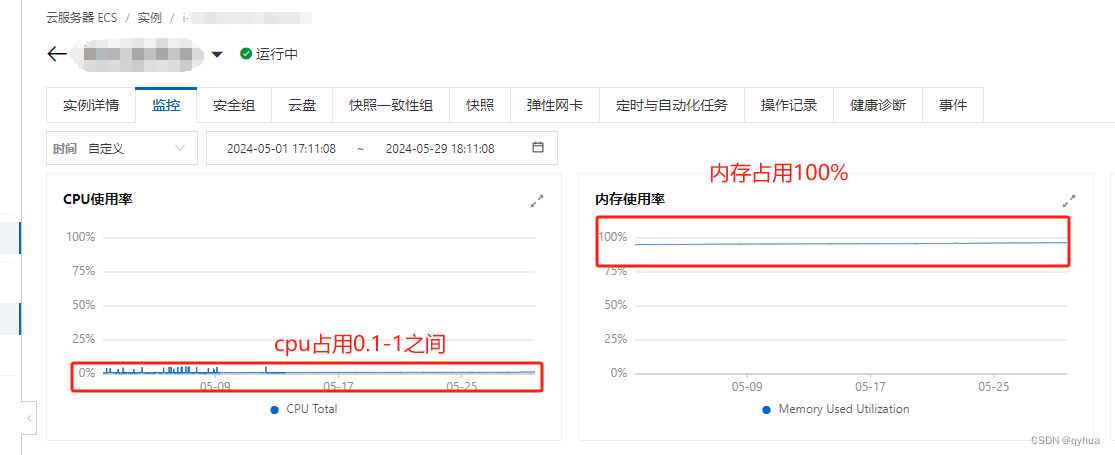
服务器内存与CPU要占用多少才合理?
一 通常服务器内存占用多少合理?cpu占用多少才合理? 1 通常配置范围建议:
建议CPU使用率不高于80%;内存使用率不高于80%; 注意:具体情况还需要根据服务器的实际负载和应用场景来判断。 2 内存使用率&…
景源畅信电商:抖音开店步骤是什么?
随着社交媒体的兴起,抖音已经成为一个不可忽视的电商平台。许多人都希望通过抖音开店来实现自己的创业梦想。那么,抖音开店的具体步骤是什么呢?接下来,我们将详细阐述这一问题。 一、明确回答问题抖音开店的步骤主要包括:注册账号…
Java基础20(文件操作 IO流 InputStream字节输入流 OutputStream字节输出流 Writer 字符输出流)
目录
一、File 文件对象
1. 创建对象
2. 相对路径和绝对路径
3. 一些方法
汇总:
获取文件信息1:
判断文件:
删除文件:
创建文件:
获取文件信息2:
4. 小结
二、IO流
1. InputStream字节输入流 …
LPDDR6带宽预计将翻倍增长:应对低功耗挑战与AI时代能源需求激增
在当前科技发展的背景下,低能耗问题成为了业界关注的焦点。国际能源署(IEA)近期报告显示,日常的数字活动对电力消耗产生显著影响——每次Google搜索平均消耗0.3瓦时(Wh),而向OpenAI的ChatGPT提出的每一次请求则消耗2.9…
利用C++与Python调用千帆免费大模型,构建个性化AI对话系统
千帆大模型已于2024年4月25日正式免费,调用这个免费的模型以实现自己的AI对话功能,遵循以下步骤:
了解千帆大模型:
千帆大模型是百度智能云推出的一个平台,提供了一系列AI能力和工具,用于快速开发和应用A…
【busybox记录】【shell指令】rmdir
目录
内容来源:
【GUN】【rmdir】指令介绍
【busybox】【rmdir】指令介绍
【linux】【rmdir】指令介绍
使用示例:
删除空目录 - 默认
删除dirname下的所有空目录,包括因删除其他目录而变为空的目录
常用组合指令:
指令不…
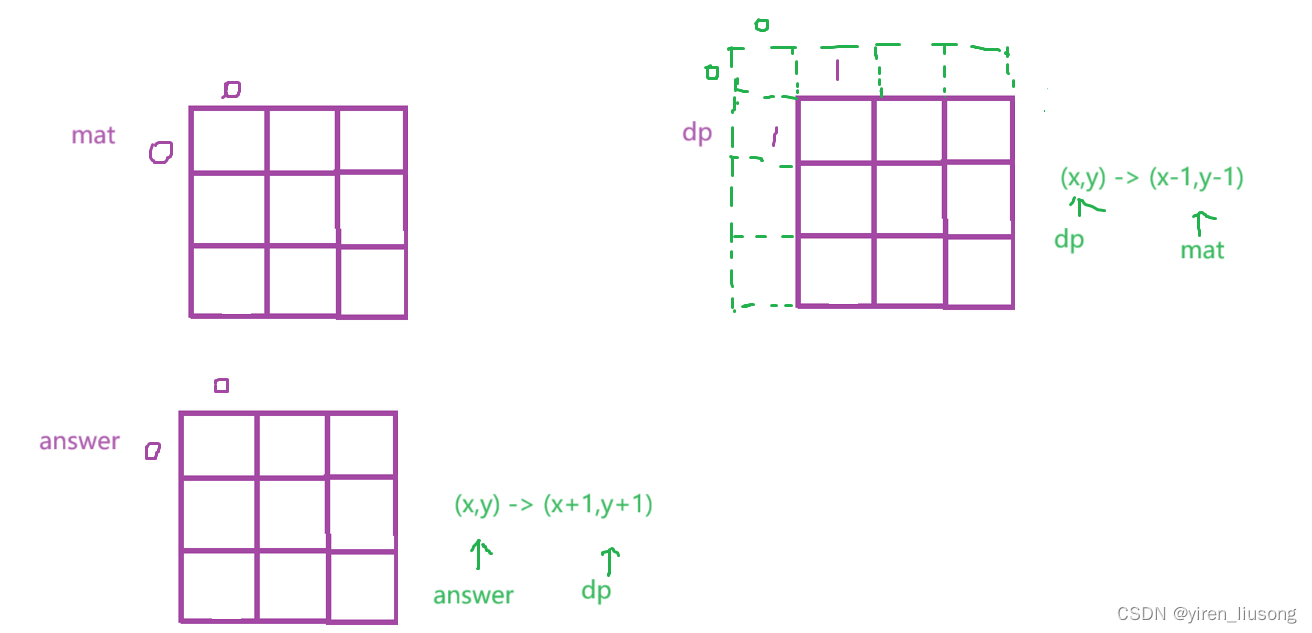
在做题中学习(62):矩阵区域和
1314. 矩阵区域和 - 力扣(LeetCode) 解法:二维前缀和
思路:读题画图才能理解意思:dun点点的是mat中的一个数,而要求的answer同位置的数 以点为中心上下左右延长 k 个单位所围成长方形的和。 因为最后answ…
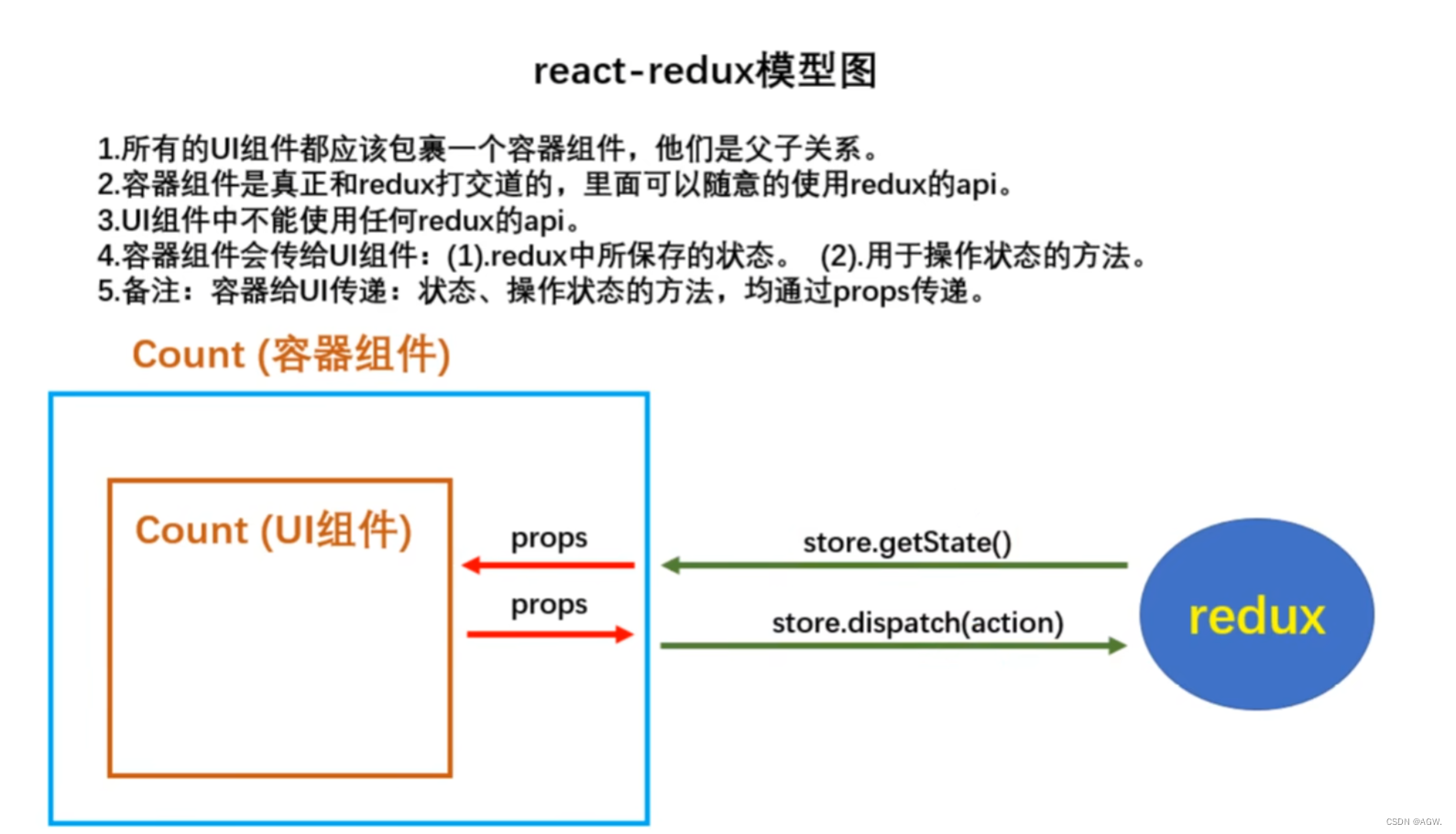
前端学习--React部分
文章目录 前端学习--React部分前言1.React简介1.1React的特点1.2引入文件1.3JSX🍉JSX简介与使用🍉JSX语法规则 1.4模块与组件🍉模块🍉组件 1.5安装开发者工具 2.React面向组件编程2.1创建组件🍉函数式组件🍉…
【数据结构:排序算法】堆排序(图文详解)
🎁个人主页:我们的五年
🔍系列专栏:数据结构课程学习
🎉欢迎大家点赞👍评论📝收藏⭐文章 目录
🍩1.大堆和小堆
🍩2.向上调整算法建堆和向下调整算法建堆:…




![[双指针] --- 快乐数 盛最多水的容器](https://img-blog.csdnimg.cn/direct/c5e6e191c4924779aaca0cf315c83c54.gif)