本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/440004.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
windows10-VMware17-Ubuntu-22.04-海康2K摄像头兼容问题,求解(已解决)
文章目录 1.webrtc camera测试2.ffmpeg 测试3.Ubuntu 自带相机4.解决办法 环境:windows10系统下,VMware的Ubuntu-22.04系统 问题:摄像头出现兼容问题,本来是想开发测试的,Ubuntu方便些。买了海康2K的USB摄像头…
NISP 一级 | 2.4 访问控制
关注这个证书的其他相关笔记:NISP 一级 —— 考证笔记合集-CSDN博客 0x01:访问控制基本概念
访问控制是针对越权使用资源的防御措施。 其目标是防止对任何资源(如计算资源、通信资源或信息资源)进行未授权的访问,从而…
RabbitMQ练习(AMQP 0-9-1 Overview)
1、What is AMQP 0-9-1
AMQP 0-9-1(高级消息队列协议)是一种网络协议,它允许遵从该协议的客户端(Publisher或者Consumer)应用程序与遵从该协议的消息中间件代理(Broker,如RabbitMQ)…
Linux find案例
目录 1. 只查找当前目录,不查找子目录中的指定文件2. 查找到的文件批量复制到指定文件夹中3. 查找到的文件批量修改所属用户和组4. 查找到的文件批量添加执行权限5. 查找到的文件内容全部导入指定文件6. 查找指定目录下指定用户所属的文件7. 获取当前目录下…
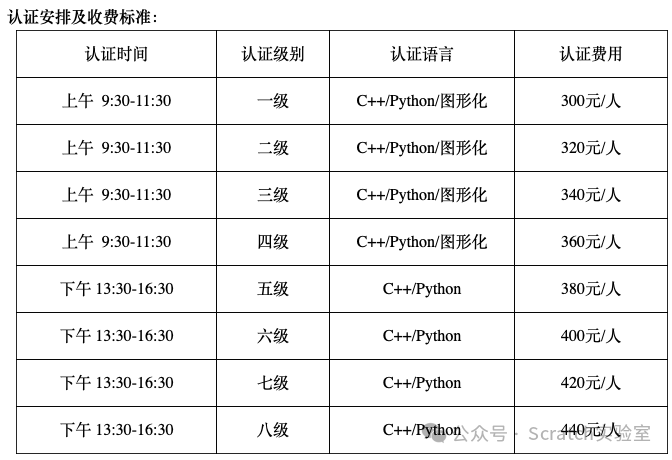
2024年第十五届蓝桥杯青少组国赛撞期GESP认证、放弃那个?
昨天蓝桥杯青少组官网发布了速查|第十五届蓝桥杯大赛青少组省赛成绩查询,首先恭喜2024年蓝桥杯青少组省赛一等奖的同学晋级蓝桥杯大赛青少组国赛,蓝桥杯青少组国赛的时间为2024年9月7日,CCF GESP编程能力等级认证也在同一天开始,同…
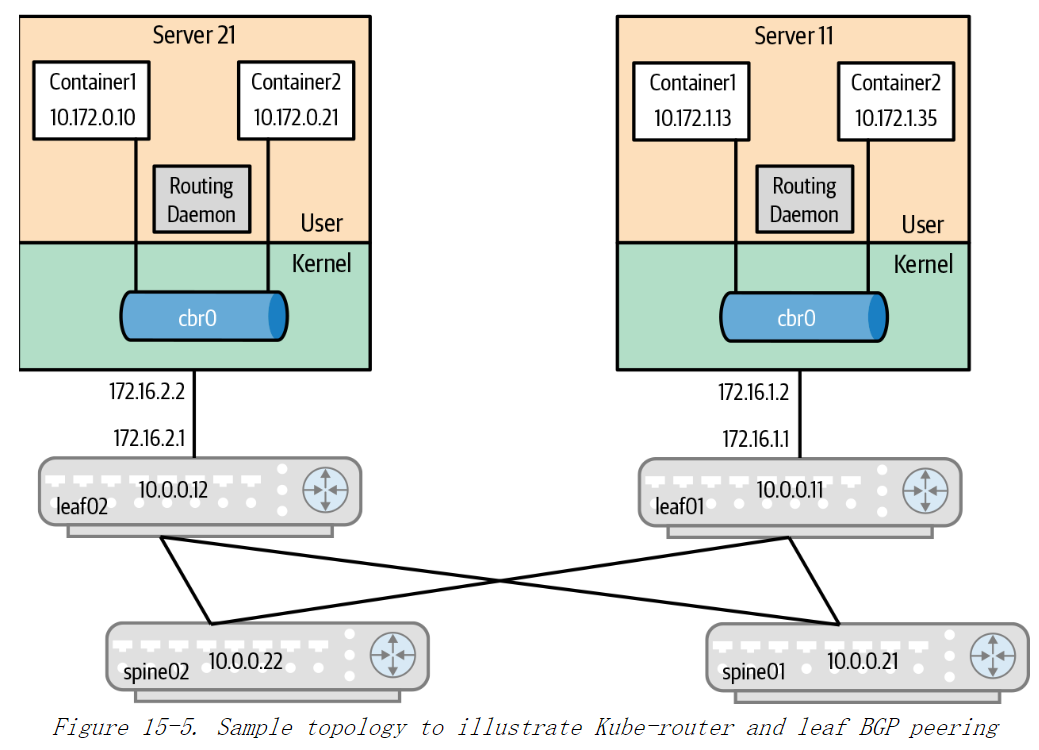
《Cloud Native Data Center Networking》(云原生数据中心网络设计)读书笔记 -- 11部署BGP
本章应有助于回答以下问题:
核心的配置概念是什么?如何为 Clos 网络配置 BGP ?无编号的 BGP 如何工作?如何配置 BGP 与主机上的 BGP 发言者 (例如 Kube-router) 建立对等关系?如何配置 BGP 以对网络进行计划维护? 核心的 BGP 配置概念
全局BGP 配置,包含:
r…
什么是 TDengine?
TDengine 是一款专为物联网、工业互联网等场景设计并优化的大数据平台,其核心模块是高性能、集群开源、云原生、极简的时序数据库。它能安全高效地将大量设备、数据采集器每天产生的高达 TB 甚至 PB 级的数据进行汇聚、存储、分析和分发,对业务运行状态进…
智能化升级:未来交流充电桩的创新之路
随着电动汽车的普及,交流充电桩作为充电基础设施的重要组成部分,其未来的发展趋势备受关注。本文将探讨交流充电桩在未来可能呈现的几个发展方向。
一、智能化升级
未来的交流充电桩将更加智能化。通过物联网技术,充电桩将能够实现远程监控…
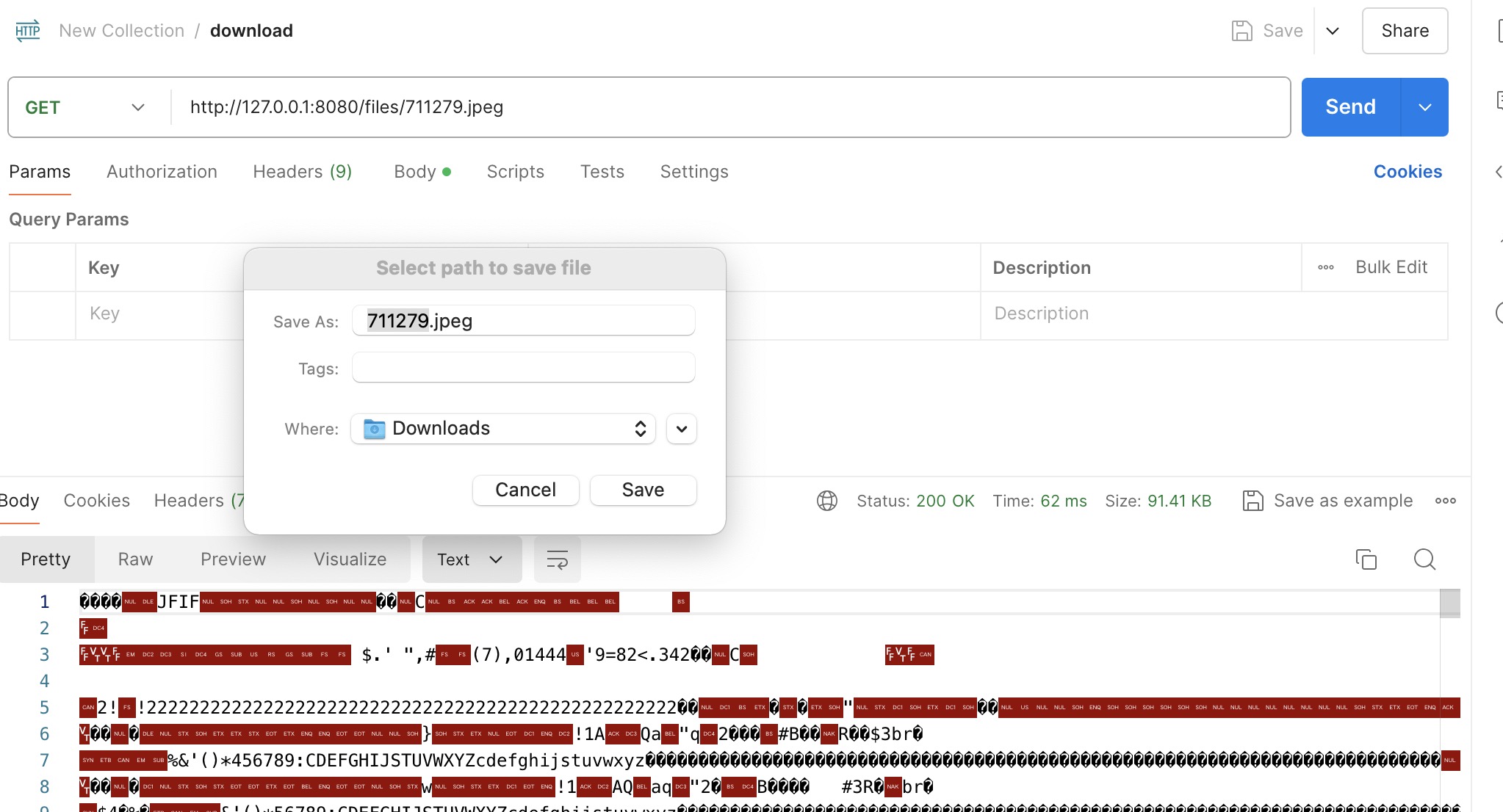
Spring Boot实现文件上传和下载
1.背景
项目中经常会有上传和下载的需求,这篇文章简述一下springboot项目中实现简单的上传和下载。
2.代码工程
实验目标 实现简单的文件上传和下载 pom.xml
<?xml version"1.0" encoding"UTF-8"?>
<project xmlns"http://…
【开发工具】探索IntelliJ IDEA插件——JSON Parser,让JSON处理变得轻松高效
开发过程中,遇到一个字符串,需要判断是否是JSON格式,或者是需要将Json字符串美化展示,是否还在打开百度搜JSON在线格式化(https://www.bejson.com/),是否还在写个main方法将字符串转成JSON格式并输出。这篇文章&#x…
Spring Boot 2.0 解决跨域问题:WebMvcConfiguration implements WebMvcConfigurer
When allowCredentials is true, allowedOrigins cannot contain the special value “*“since that cannot When allowCredentials is true, allowedOrigins cannot contain thespecial value "*"since that cannot be set on the “Access-Control-Allow-Origin”…
Level3 — PART 3 — 自然语言处理与文本分析
目录
自然语言处理概要
分词与词性标注
N-Gram 分词
分词及词性标注的难点
法则式分词法
全切分
FMM和BMM
Bi-direction MM
优缺点
统计式分词法
N-Gram概率模型
HMM概率模型
词性标注(Part-of-Speech Tagging)
HMM
文本挖掘概要
信息检索(Information Retr…
模版方法模式template method
学习笔记,原文链接 https://refactoringguru.cn/design-patterns/template-method
超类中定义了一个算法的框架, 允许子类在不修改结构的情况下重写算法的特定步骤。 上层接口有默认实现的方法和子类需要自己实现的方法
多模态大模型: 盘点Highlights part2——Qwen-VL系列
前言 Hi大家好,我叫延捷,是一名计算机视觉算法工程师,也是叉烧的老朋友了。我们计划发布一系列关于多模态大模型的文章,帮助大家快速、精准地了解多模态大模型的前世今生,并且深入各个多模态大模型领域优秀的工作&…
原型模式prototype
此篇为学习笔记,原文链接 https://refactoringguru.cn/design-patterns/prototype
能够复制已有对象, 而又无需使代码依赖它们所属的类
所有的原型类都必须有一个通用的接口, 使得即使在对象所属的具体类未知的情况下也能复制对象。 原型对…
ubuntu上通过openvswitch卸载实现roce over vxlan
环境
操作系统:
uname -a
Linux 5.4.0-187-generic #207-Ubuntu SMP Mon Jun 10 08:16:10 UTC 2024 x86_64 x86_64 x86_64 GNU/Linux Mellanox网卡:
ethtool -i ens6np0
driver: mlx5_core
version: 23.10-2.1.3
firmware-version: 20.39.3004 (MT_0…
FreeRTOS实战指南 — 1 FreeRTOS简介
目录
1.1 为什么需要FreeRTOS
1.2 FreeRTOS资料获取
1.3 FreeRTOS文件夹内容 1.1 为什么需要FreeRTOS
裸机开发直接控制硬件,虽然资源占用少,但开发复杂性高,缺乏高级功能,适合资源受限的简单应用。嵌入式操作系统提供了硬件抽…
工厂ERP管理系统实现源码(JAVA)
工厂进销存管理系统是一个集采购管理、仓库管理、生产管理和销售管理于一体的综合解决方案。该系统旨在帮助企业优化流程、提高效率、降低成本,并实时掌握各环节的运营状况。 在采购管理方面,系统能够处理采购订单、供应商管理和采购入库等流程ÿ…
TitleBar:打造高效Android标题栏的新选择
在Android应用开发中,标题栏是用户界面的重要组成部分。一个好的标题栏不仅能够提升应用的专业感,还能增强用户体验。然而,传统的标题栏实现方式往往存在代码冗余、样式不统一、性能开销大等问题。今天,我们将介绍一个名为TitleBa…
数据结构与算法03 顺序表+链表
注意点:
函数的定义中建议增加断言:结构体指针不能为NULL!(空指针不能接引用!)控制台退出后显示的代码只要不为0,就不是正常退出!Vs中编辑 -> 高级 -> 查看空白 可以…