本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/440015.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
分解+优化+组合+对比!核心无忧!VMD-SSA-Transformer-LSTM多变量时间序列光伏功率预测
分解优化组合对比!核心无忧!VMD-SSA-Transformer-LSTM多变量时间序列光伏功率预测 目录 分解优化组合对比!核心无忧!VMD-SSA-Transformer-LSTM多变量时间序列光伏功率预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍
1.…
鸿蒙开发笔记_电商严选01_登录页面(静态页面)
由于上班较忙,抽空闲暇时间,快速更新中。。。 效果图 登录页面(静态页面) import CommonConstants from ./CommonConstants;/*** 登录页面*/
// 输入文本框,的自定义样式扩展
// @Extend装饰器表示继承、扩展的意思。这里代表:自定义样式扩展
@Extend(TextInput)
functio…
Python OpenCV精讲系列 - 入门指南(一)
💖💖⚡️⚡️ 专栏:Python OpenCV精讲 ⚡️⚡️💖💖 本专栏聚焦于Python结合OpenCV库进行计算机视觉开发的专业教程。通过系统化的课程设计,从基础概念入手,逐步深入到图像处理、特征检测、物体…
142. Go操作Kafka(confluent-kafka-go库)
文章目录 Apache kafka简介开始使用Apache Kafka构建生产者构建消费者 总结 之前已经有两篇文章介绍过
Go如何操作
kafka 28.windows安装kafka,Go操作kafka示例(sarama库) 51.Go操作kafka示例(kafka-go库) Apache ka…
数学建模笔记—— 线性规划
数学建模笔记—— 线性规划 线性规划1. 模型引出1.1 线性规划模型的三要素1.2 线性规划模型建立步骤1.3 线性规划的表现形式1.4 线性规划的模型特点 2.典型例题3. python代码求解3.1 求解KK升级的问题3.2 求解投资收益问题 线性规划
在人们的生产实践中,经常会遇到…
Android Studio下载Gradle失败问题解决
问题说明
使用 Android Studio 构建程序报错如下
Could not install Gradle distribution from https://services.gradle.org/distributions/gradle-7.5.1-bin.zip.
Reason: java.net.SocketTimeoutException: Connect timed out问题解决
下载对应版本的压缩包 gradle-7.5.1…
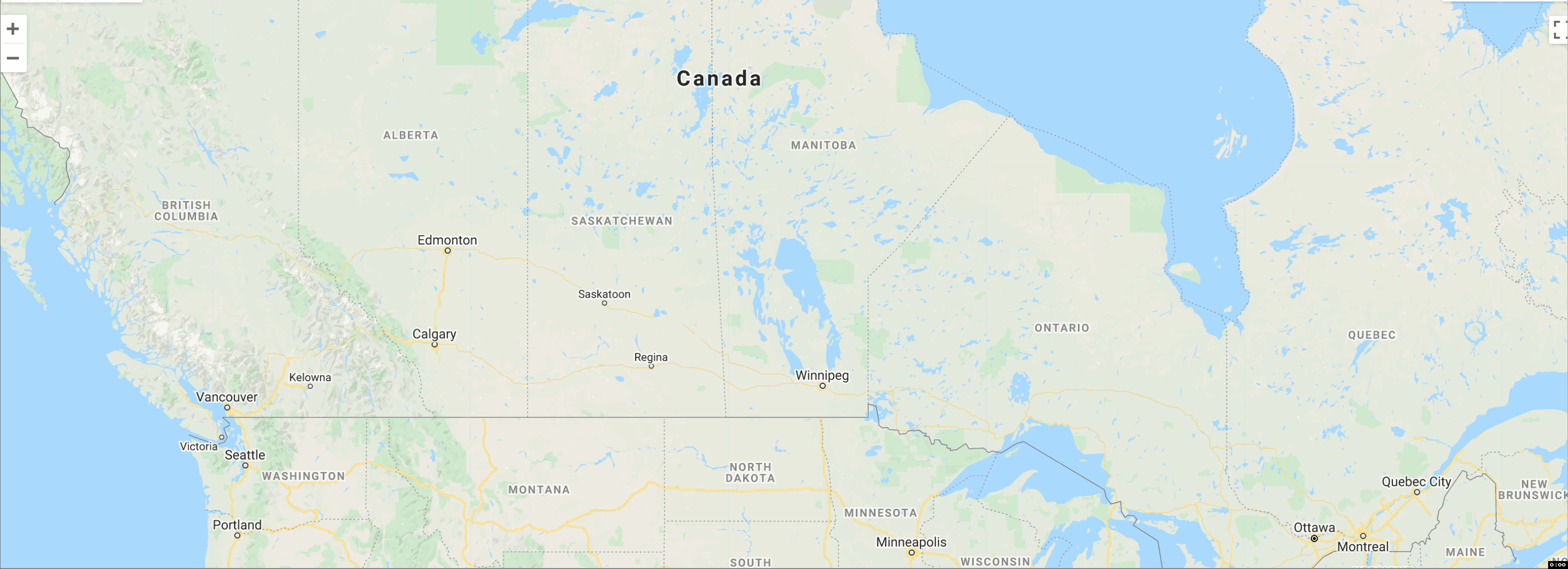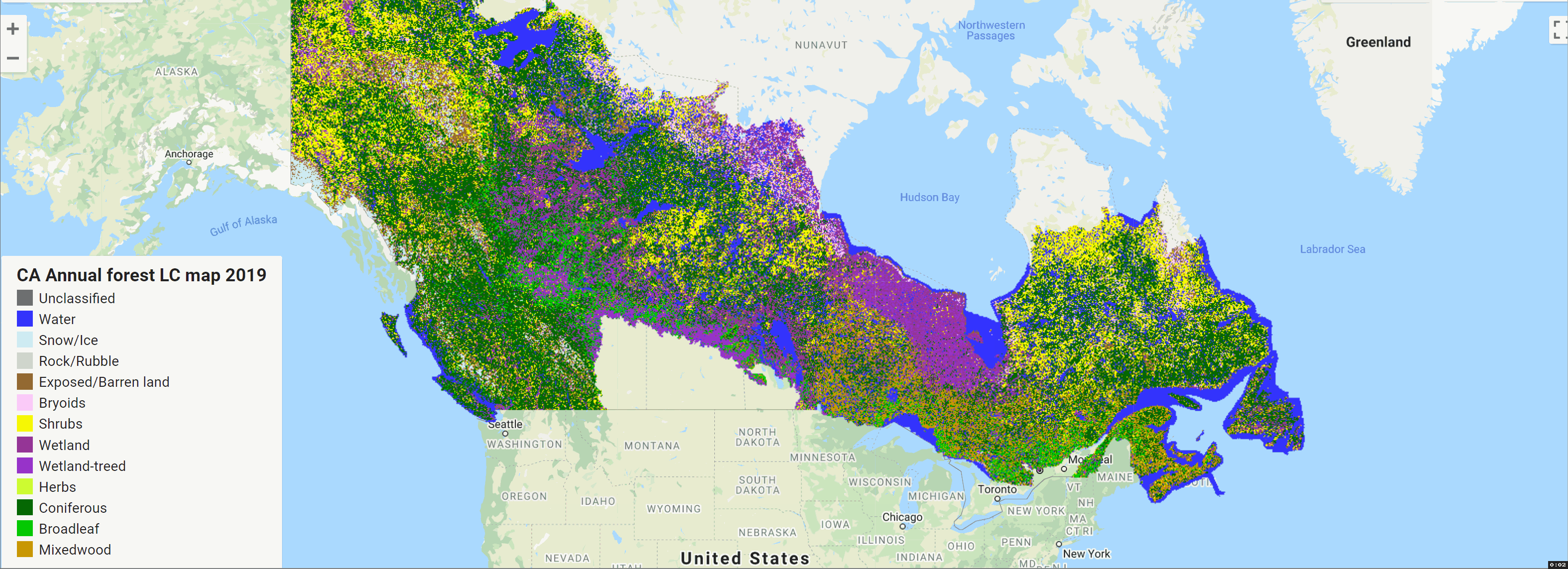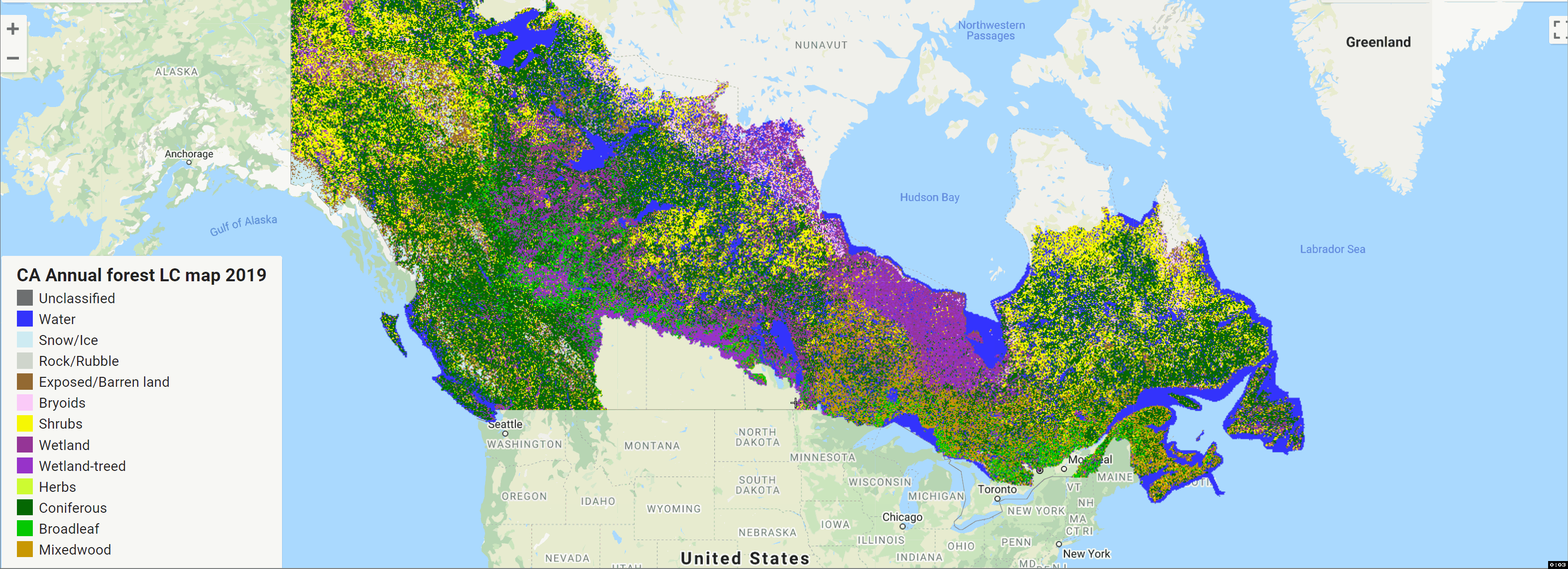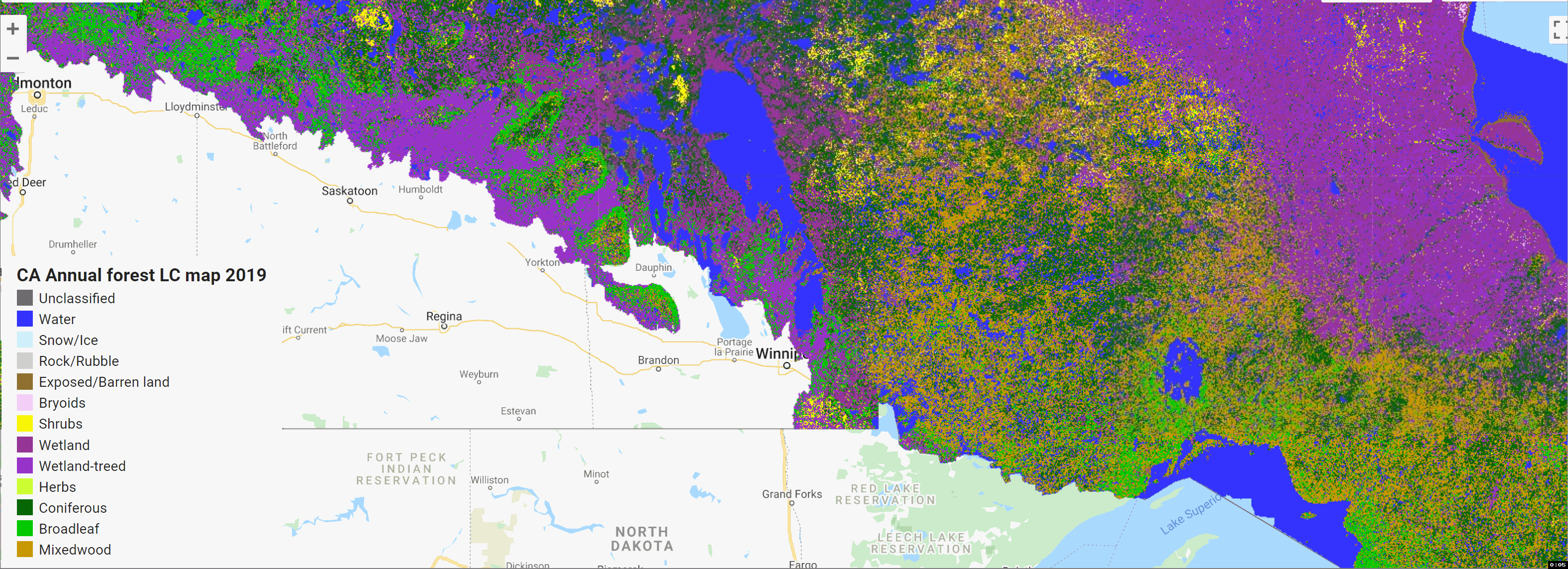
GEE数据集:加拿大森林生态系统高分辨率年度林地覆盖图(1984-2022 年)
目录 加拿大森林生态系统高分辨率年度林地覆盖图(1984-2022 年)
简介
数据集说明
空间信息
分类结果
代码
代码链接
引用
许可
网址推荐
0代码在线构建地图应用
机器学习 加拿大森林生态系统高分辨率年度林地覆盖图(1984-2022 年&…
0基础跟德姆(dom)一起学AI Python进阶09-算法和数据结构
* 数据结构介绍 * 列表 * 链表 * 算法介绍 * 排序相关(冒泡, 插入, 选择, 快速排序)
---
1.数据结构和算法简介
* 程序 大白话翻译, **程序 数据结构 算法**
* 数据结构 指的是 **存储, 组织数据的方式.**
* 算法 指的是 **为了解决实际业务问题而思考 思路和方法…
生信圆桌x生信分析平台:助力生物信息学研究的综合工具
介绍 少走弯路,高效分析;了解生信云,访问 【生信圆桌x生信专用云服务器】 : www.tebteb.cc
生物信息学的迅速发展催生了众多生信分析平台,这些平台通过集成各种生物信息学工具和算法,极大地简化了数据处理和分析流程,使研究人员能够更高效地…
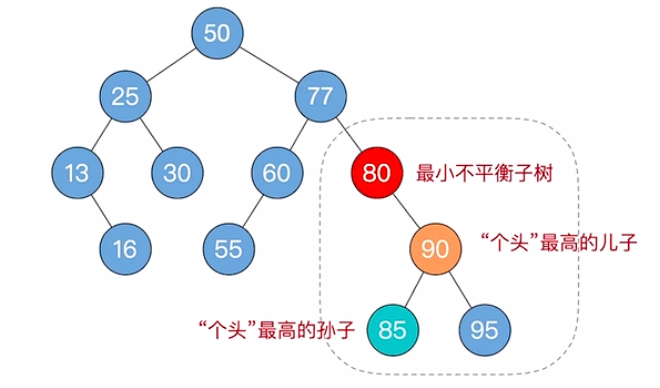
数据结构基础详解(C语言): 树与二叉树的应用_哈夫曼树与哈夫曼曼编码_并查集_二叉排序树_平衡二叉树
文章目录 树与二叉树的应用1.哈夫曼树与哈夫曼曼编码1.1 带权路径长度1.2 哈夫曼树1.2.1 哈夫曼树的构造1.3 哈夫曼编码 2.并查集2.1 并查集的三要素2.1.1 并查集的逻辑结构2.1.2 并查集的存储结构 2.2 并查集的优化2.2.1 初步优化(并操作优化)2.2.2 终极…
windows10-VMware17-Ubuntu-22.04-海康2K摄像头兼容问题,求解(已解决)
文章目录 1.webrtc camera测试2.ffmpeg 测试3.Ubuntu 自带相机4.解决办法 环境:windows10系统下,VMware的Ubuntu-22.04系统 问题:摄像头出现兼容问题,本来是想开发测试的,Ubuntu方便些。买了海康2K的USB摄像头…
NISP 一级 | 2.4 访问控制
关注这个证书的其他相关笔记:NISP 一级 —— 考证笔记合集-CSDN博客 0x01:访问控制基本概念
访问控制是针对越权使用资源的防御措施。 其目标是防止对任何资源(如计算资源、通信资源或信息资源)进行未授权的访问,从而…
RabbitMQ练习(AMQP 0-9-1 Overview)
1、What is AMQP 0-9-1
AMQP 0-9-1(高级消息队列协议)是一种网络协议,它允许遵从该协议的客户端(Publisher或者Consumer)应用程序与遵从该协议的消息中间件代理(Broker,如RabbitMQ)…
Linux find案例
目录 1. 只查找当前目录,不查找子目录中的指定文件2. 查找到的文件批量复制到指定文件夹中3. 查找到的文件批量修改所属用户和组4. 查找到的文件批量添加执行权限5. 查找到的文件内容全部导入指定文件6. 查找指定目录下指定用户所属的文件7. 获取当前目录下…
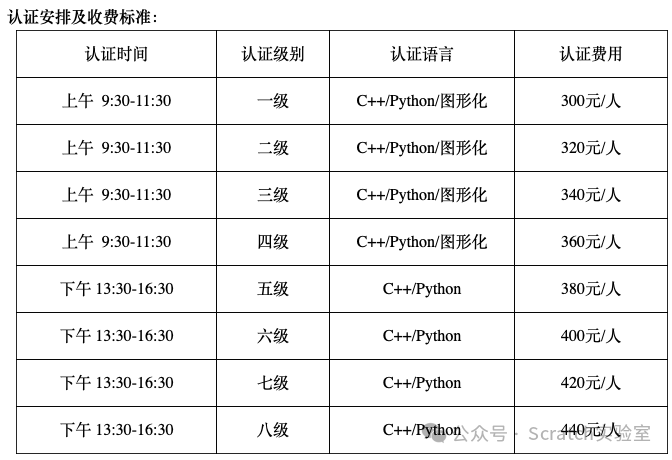
2024年第十五届蓝桥杯青少组国赛撞期GESP认证、放弃那个?
昨天蓝桥杯青少组官网发布了速查|第十五届蓝桥杯大赛青少组省赛成绩查询,首先恭喜2024年蓝桥杯青少组省赛一等奖的同学晋级蓝桥杯大赛青少组国赛,蓝桥杯青少组国赛的时间为2024年9月7日,CCF GESP编程能力等级认证也在同一天开始,同…
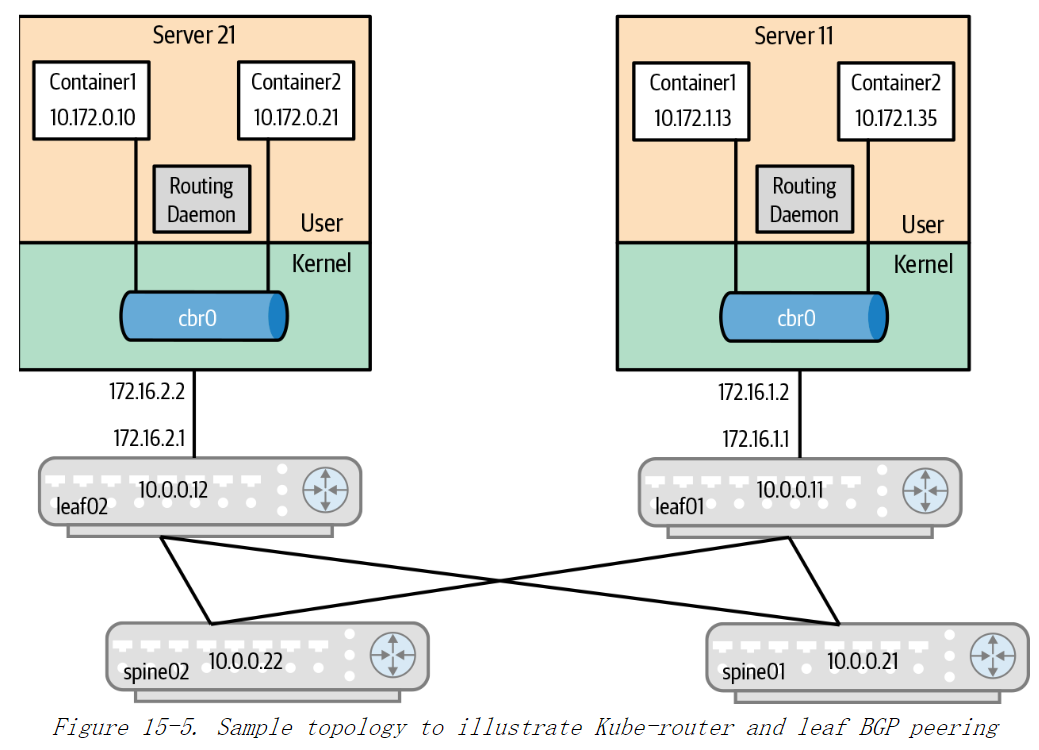
《Cloud Native Data Center Networking》(云原生数据中心网络设计)读书笔记 -- 11部署BGP
本章应有助于回答以下问题:
核心的配置概念是什么?如何为 Clos 网络配置 BGP ?无编号的 BGP 如何工作?如何配置 BGP 与主机上的 BGP 发言者 (例如 Kube-router) 建立对等关系?如何配置 BGP 以对网络进行计划维护? 核心的 BGP 配置概念
全局BGP 配置,包含:
r…
什么是 TDengine?
TDengine 是一款专为物联网、工业互联网等场景设计并优化的大数据平台,其核心模块是高性能、集群开源、云原生、极简的时序数据库。它能安全高效地将大量设备、数据采集器每天产生的高达 TB 甚至 PB 级的数据进行汇聚、存储、分析和分发,对业务运行状态进…
智能化升级:未来交流充电桩的创新之路
随着电动汽车的普及,交流充电桩作为充电基础设施的重要组成部分,其未来的发展趋势备受关注。本文将探讨交流充电桩在未来可能呈现的几个发展方向。
一、智能化升级
未来的交流充电桩将更加智能化。通过物联网技术,充电桩将能够实现远程监控…
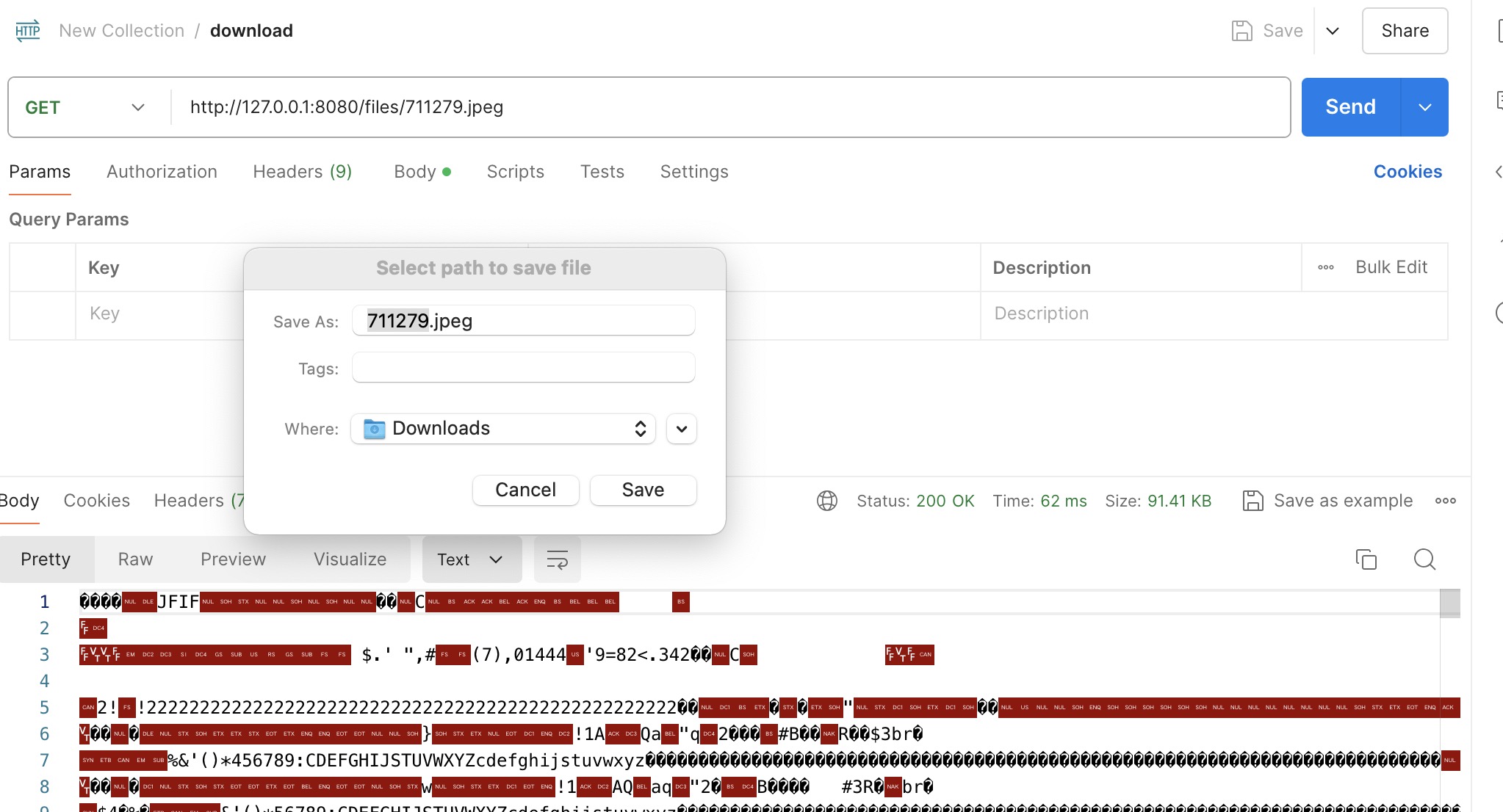
Spring Boot实现文件上传和下载
1.背景
项目中经常会有上传和下载的需求,这篇文章简述一下springboot项目中实现简单的上传和下载。
2.代码工程
实验目标 实现简单的文件上传和下载 pom.xml
<?xml version"1.0" encoding"UTF-8"?>
<project xmlns"http://…