本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/443679.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Android插件化(三)基础之Android应用程序资源的编译和打包过程分析
Android插件化(三)基础之Android应用程序资源的编译和打包过程分析
Android资源加载常规思路
getResourcesForApplication
//首先,通过包名获取该包名的Resources对象
Resources res pm.getResourcesForApplication(packageName);
//根据约定好的名字,…
少儿编程小游戏 | Scratch《物理投篮》
在线玩:Scratch少儿编程游戏 : 《物理投篮》免费下载-小虎鲸Scratch资源站 在Scratch编程的世界里,孩子们不仅能学习编程知识,还能通过动手实践开发有趣的小游戏。而今天要介绍的这款少儿编程小游戏——《物理投篮》,正是一个集趣…
2024重生之回溯数据结构与算法系列学习【无论是王道考研人还真爱粉都能包会的;不然别给我家鸽鸽丢脸好嘛?】
目录 数据结构王道第2章之顺序表 顺序表的定义和基本操作 定义: 基本操作: 基本操作: 编辑 顺序表的实现-静态分配编辑 顺序表的静态分配初始化 如果“数组”存满了怎么办: 顺序表的实现-动态分配: 编辑 顺序表…
mysql使用sql函数对json数组的处理
MySQL从5.7版本开始增加了对JSON数据类型的支持。你可以使用->>操作符和JSON_EXTRACT函数来访问JSON数据中的值。
但是,对于JSON数组,如果你想要获取数组中的所有元素,MySQL并没有直接的函数来返回数组中的所有元素作为单独的行。不过…
【网络原理】Tcp 常用提升效率机制——滑动窗口,快速重传,流量控制, 拥塞控制, 建议收藏 !!!
本篇会加入个人的所谓鱼式疯言
❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言
而是理解过并总结出来通俗易懂的大白话,
小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的.
🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人…
[网络层]-IP协议相关特性
IP协议
基本概念
主机 : 配有IP地址,但是不进行路由控制的设备路由器 : 既配有IP地址,又能进行路由控制节点: 主机和路由器的统称
协议头格式 4位版本(version):占四位,用于指定IP协议的版本,例如,使用IPv4,该字段就为44位首部长度: 表示IP协议首部的长度,以32位bit (4字节)…
Redis(redis基础,SpringCache,SpringDataRedis)
文章目录 前言一、Redis基础1. Redis简介2. Redis下载与安装3. Redis服务启动与停止3 Redis数据类型4. Redis常用命令5. 扩展数据类型 二、在Java中操作Redis1. Spring Data Redis的使用1.1. 介绍1.2. 环境搭建1.3. 编写配置类,创建RedisTemplate对象1.4. 通过Redis…
CICD 持续集成与持续交付
目录
一 CICD是什么
1.1 持续集成(Continuous Integration)
1.2 持续部署(Continuous Deployment)
1.3 持续交付(Continuous Delivery)
二 git工具使用
2.1 git简介
2.2 git 工作流程
三 部署git
…
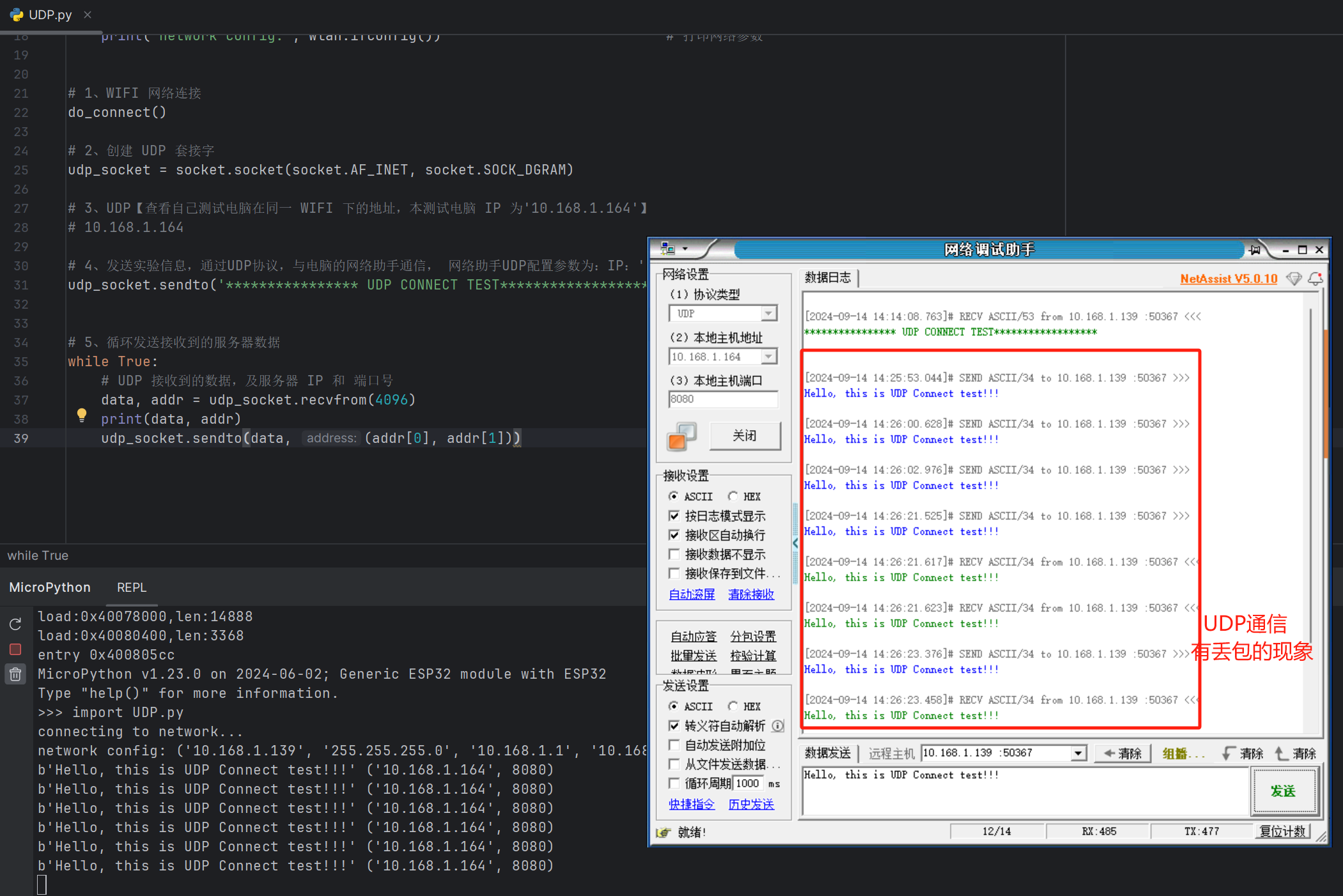
10 - UDP实验
在本章节中,我们将采用 network 与 socket 这两个第三方库来构建UDP网络连接的功能。具体而言,network 库将被应用于WiFi连接的建立,而 socket 库则基于 lwIP 协议栈来实现网络协议的连接。在实验环节,我们将利用 ESP32 开发板与远…
【吊打面试官系列-MySQL面试题】CHAR 和 VARCHAR 的区别?
大家好,我是锋哥。今天分享关于【CHAR 和 VARCHAR 的区别?】面试题,希望对大家有帮助; CHAR 和 VARCHAR 的区别? 1、CHAR 和 VARCHAR 类型在存储和检索方面有所不同 2、CHAR 列长度固定为创建表时声明的长度…
Java项目实战II基于Java+Spring Boot+MySQL的校园社团信息管理系统(源码+数据库+文档)
目录
一、前言
二、技术介绍
三、系统实现
四、论文参考
五、核心代码
六、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者,专注于大学生项目实战开发、讲解和毕业答疑辅导。获取源码联系方式请查看文末 一、前言
在当今高校…
【Tomcat源码分析】启动过程深度解析 (二)
前言
前文已述,Tomcat 的初始化由 Bootstrap 反射调用 Catalina 的 load 方法完成,包括解析 server.xml、实例化各组件、初始化组件等步骤。此番,我们将深入探究 Tomcat 如何启动 Web 应用,并解析其加载 ServletContextListener …
Linux与Ubuntu:内核与发行版的关系
在计算机科学的领域内,Linux和Ubuntu这两个术语频繁出现,但它们之间的确切联系往往不为大众所熟知。本文旨在深入探讨Linux内核与Ubuntu操作系统发行版之间的技术关系,并阐明它们各自的独特性质。
Linux内核:操作系统的基石
Lin…
CenterPoint-KITTI:环境配置、模型训练、效果展示;KITTI 3D 目标检测数据集下载
目录
前言
Python虚拟环境创建以及使用
KITTI3D目标检测数据集
CenterPoint-KITTI编译遇到问题合集
ImportError: cannot import name VoxelGenerator from spconv.utils
失败案例
最终解决方案
对于可选参数,road plane的处理
E: Unable to locate packag…
使用gitee如何回滚上一个版本,简单操作方式-gitee自带功能无需使用代码
使用gitee如何回滚上一个版本,简单操作方式-gitee自带功能无需使用代码,很多朋友使用代码的话容易出错,gitee自带了本功能: 找到gitee代码仓库,找到对应的想要回滚的版本点击进去 点击revert,选择自己对应的…
Git使用教程-将idea本地文件配置到gitte上的保姆级别步骤
🤹♀️潜意识起点:个人主页
🎙座右铭:得之坦然,失之淡然。
💎擅长领域:前端
是的,我需要您的:
🧡点赞❤️关注💙收藏💛
是我持…
微信支付开发-前端api实现
一、操作流程图 二、代码实现
<?php
/*** 数字人答题业务流* User: 龙哥三年风水* Date: 2024/9/11* Time: 14:59*/
namespace app\controller\shuziren;
use app\controller\Base;
use app\model\param\QuestionParam as PQPModel;
use app\model\answer\QuestionBank;
u…
人工智能(AI)的影响下人类的生活样子
讨论在人工智能(AI)的影响下人类的生活是什么样子
在21世纪的今天,人工智能(AI)已经不再是遥不可及的未来科技,而是悄然渗透到我们日常生活的每一个角落,以一种前所未有的方式改变着我们的生活方式、工作模式乃至社会…






![[网络层]-IP协议相关特性](https://i-blog.csdnimg.cn/direct/6de05440b0a441ac839e5cbfd4c9ddd4.png)