本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/438551.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
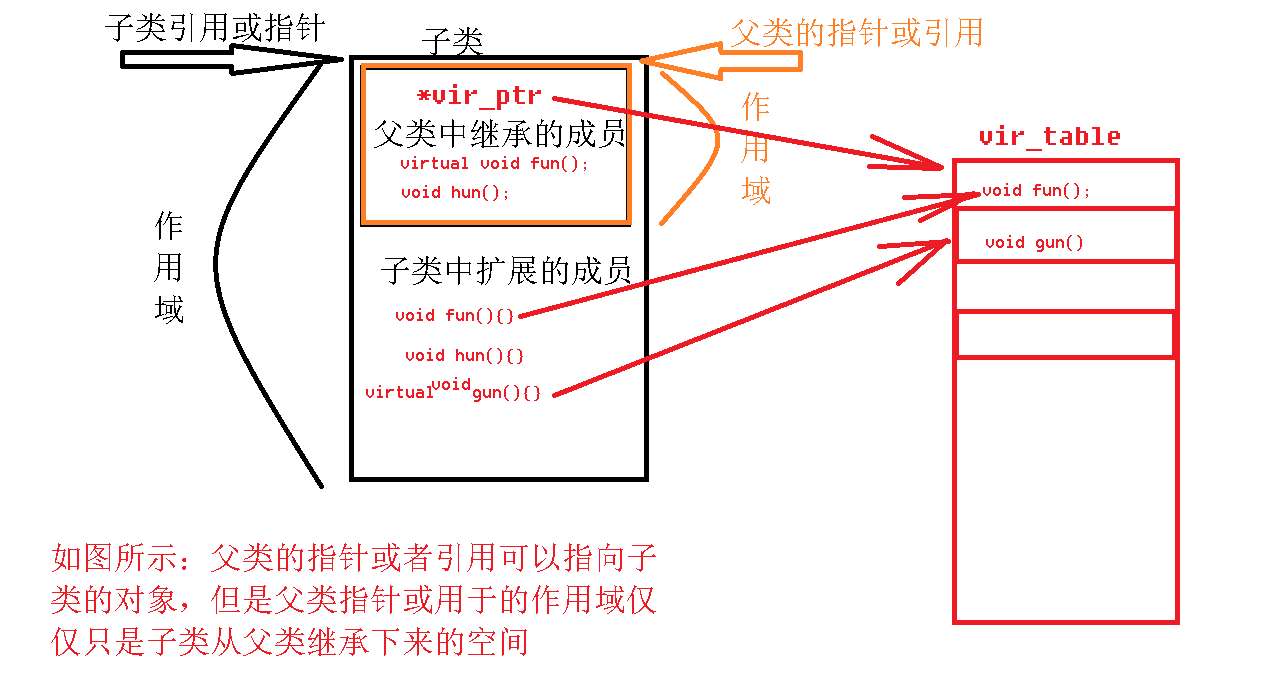
day47——面向对象特征之继承
一、继承(inhert)
面向对象三大特征:封装、继承、多态
继承:所谓继承,是类与类之间的关系。就是基于一个已有的类,来创建出一个新类的过程叫做继承。主要提高代码的复用性。
1.1 继承的作用
1> 实现…
Windows conda常用方法
这里写目录标题 conda链接jupyter conda链接jupyter
列出当前所有环境: conda env list 创建新环境: conda create -n your_env_name pythonX.X(2.7、3.6、3.8等) 激活环境: conda activate your_env_name 链接jupyte…
VXLAN 为何采用UDP
VXLAN 简介
VXLAN是一种网络虚拟化技术,它通过在UDP数据包中封装MAC地址和IP信息,使得二层网络(如以太网)能够跨越三层网络(如IP网络)进行扩展。这种封装方式不仅支持TCP流量的传输,还能有效处…
SpringCloud开发实战(四):Feign远程调用
目录 SpringCloud开发实战(一):搭建SpringCloud框架 SpringCloud开发实战(二):通过RestTemplate实现远程调用 SpringCloud开发实战(三):集成Eureka注册中心 Feign简介
我…
机器学习(五) -- 监督学习(8) --神经网络1
机器学习系列文章目录及序言深度学习系列文章目录及序言
上篇:机器学习(五) -- 无监督学习(2) --降维2 下篇:机器学习(五) -- 监督学习(8) --神经网络2 前言…
基于SSM+MySQL的医院在线挂号系统
系统背景 在当前数字化转型浪潮的推动下,医疗服务行业正经历着前所未有的变革。随着人口老龄化的加剧、患者就医需求的日益增长以及医疗资源分布不均等问题的凸显,传统的就医模式已难以满足患者对于便捷、高效医疗服务的需求。因此,构建一套基…
设计模式 —— 单例模式
文章目录 一、单例模式1.1 单例模式定义1.2 单例模式的优点1.3 单例模式的缺点1.4 单例模式的使用场景 二、普通案例2.1 饿汉式单例模式(Eager Initialization Singleton)2.2 懒汉式单例模式(Lazy Initialization Singleton) 参考资料 本文源代码地址为 java-demos/singeleton-…
探索未来科技发展:芯片设计的创新之路
在当今这个日新月异的数字时代,芯片设计作为信息技术的核心驱动力,正以前所未有的速度推动着社会进步与产业升级。作为科技领域的璀璨明珠,芯片设计不仅关乎数据处理的速度与效率,更是人工智能、物联网、云计算等技术得以实现的基…
Docker 详解及详细配置讲解
Docker 简介 2008 年LXC(LinuX Contiainer)发布,但是没有行业标准,兼容性非常差 docker2013年首次发布,由Docker, Inc开发 什么是 Docker
Docker是管理容器的引擎,为应用打包、部署平台,而非单纯的虚拟化技术…
不小心删除丢失了所有短信?如何在 iPhone 上查找和恢复误删除的短信
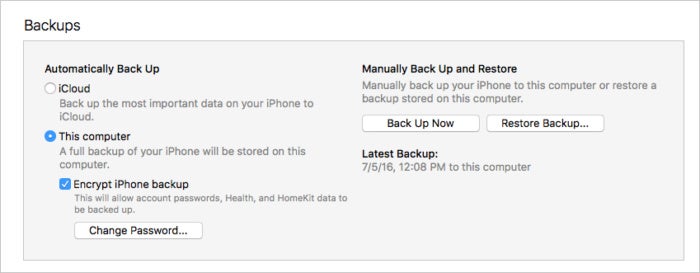
不小心删除了一条短信,或者丢失了所有短信?希望还未破灭,下面介绍如何在 iPhone 上查找和恢复已删除的短信。
短信通常都是非正式和无关紧要的,但短信中可能包含非常重要的信息。因此,如果您删除了一些短信以清理 iPh…
Python画笔案例-032 绘制螺旋扇子
1、绘制螺旋扇子
通过 python 的turtle 库绘螺旋扇子图,如下图: 2、实现代码 绘制螺旋扇子,以下为实现代码:
"""螺旋扇子.py
"""
import turtle
from coloradd import * # 从coloradd命令导…
win12R2安装.NET Framework 3.5
一丶安装原因
因此插件的缺失, 有些软件或系统不支持安装.
二丶安装步骤
1丶下载.NET Framework 3.5 点击插件下载, 提取码: 1995, 下载完成之后解压到想要安装的位置上. 2丶打开 服务器管理器 3丶点击: 管理 -> 添加角色和功能 4丶点击下一步到服务器角色, 选择web服…
版本控制的核心:Git中的哈希与默克尔树解析
Git是最常用的代码版本控制工具。它帮助我们跟踪代码的更改、管理代码版本,同时保证代码库的完整性和安全性。我们知道 Git 中有一些基本的操作,比如commit、merge、rebase等,但这些操作的底层机制是如何实现的呢?哈希函数和默克尔…
计算机毕业设计Spark+PyTorch知识图谱房源推荐系统 房价预测系统 房源数据分析 房源可视化 房源大数据大屏 大数据毕业设计 机器学习
《SparkPyTorch知识图谱房源推荐系统》开题报告
一、选题背景与意义
1.1 选题背景
随着互联网的快速发展和大数据技术的广泛应用,房地产行业特别是房屋租赁市场迎来了前所未有的变革。房源信息的海量增长使得用户在寻找合适的房源时面临巨大挑战。传统的房源推荐…
电路分析 ---- 电平移位电路
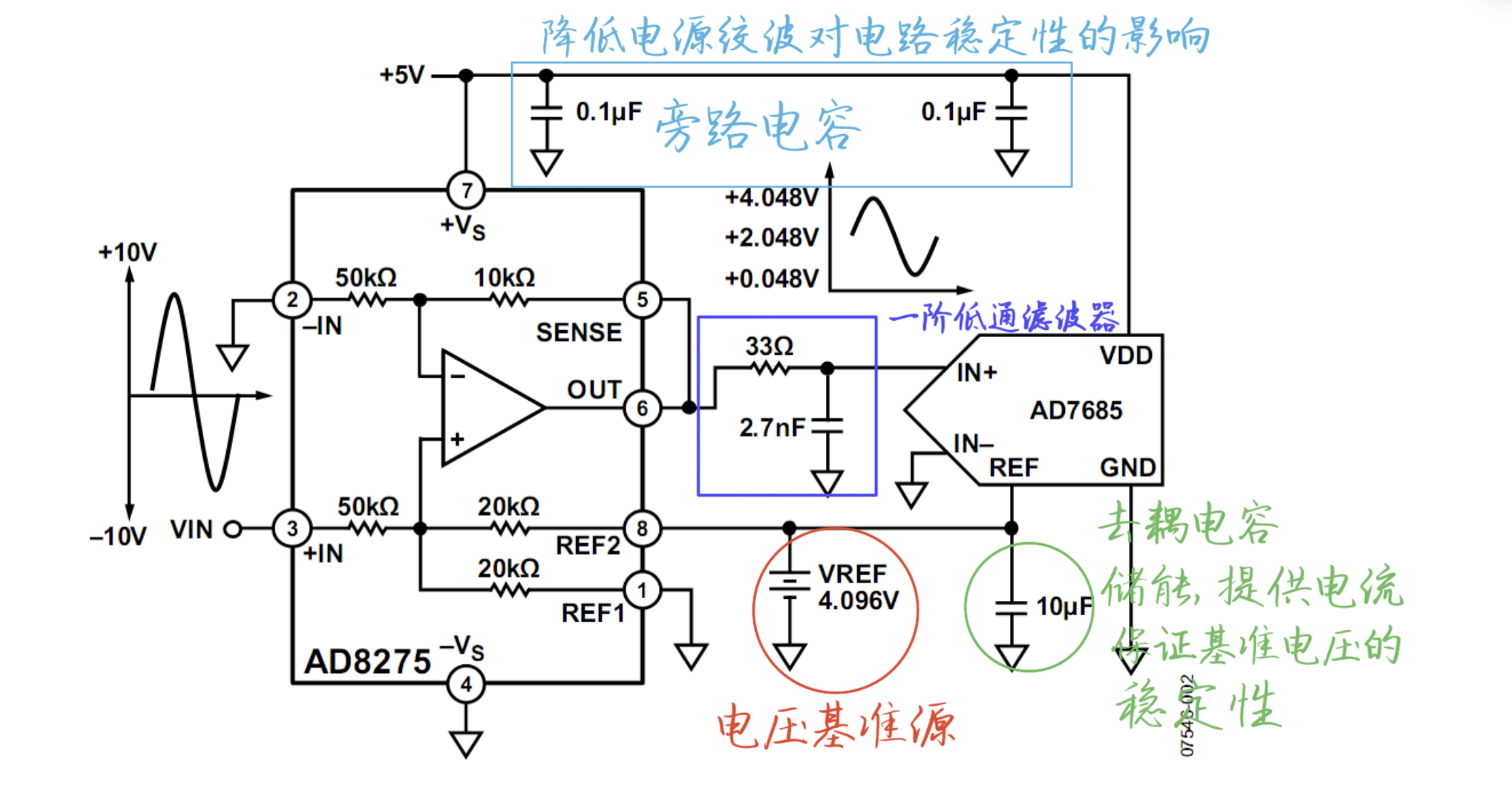
1 电平移位电路
如图所示的电平移位电路,用于ADC的前级驱动,它将一个变化范围为-10V ~ 10V的输入信号,线性变化成0.048V ~ 4.048V的信号,以满足ADC的输入范围要求。
2 电路说明 V R E F V_{REF} VREF为电压基准源,…
轻量级模型解读——MobileNet系列
MobileNet系列到现在2024年,已经出到了第四个版本,分别如下: 2017年MobileNetv1——>2018年MobileNetv2——>2019年MobileNetv3——>2024年MobileNetv4,下面简要概述一下几个版本的改进部分。 目录 1、MobileNetv12、Mob…
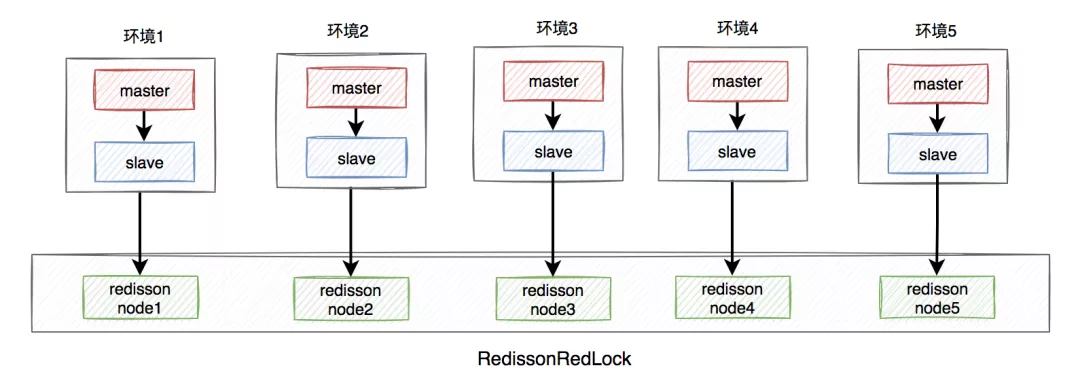
聊聊Redis分布式锁的八大坑
前言
在分布式系统中,由于redis分布式锁相对于更简单和高效,成为了分布式锁的首先,被我们用到了很多实际业务场景当中。
但不是说用了redis分布式锁,就可以高枕无忧了,如果没有用好或者用对,也会引来一些…
JavaEE-HTTPHTTPS
目录 HTTP协议
一、概念
二、http协议格式
http请求报文
http响应报文
URL格式
三、认识方法
四、认识报头
HTTP响应中的信息
HTTPS协议
对称加密
非对称加密
中间人攻击
解决中间人攻击 HTTP协议
一、概念 HTTP (全称为 "超⽂本传输协议") 是⼀种应⽤…